主要是联系一下数学中的梯度和深度学习中梯度的关系
什么是梯度
梯度是一个向量,有大小有方向
大小:梯度的模等于在该点可以取到的最大的变化率
方向:该点处取变化最大值时的那个方向
用来干什么?
可以用来快速找到多维变量函数的极值,在深度学习中一般是寻找损失函数的最小值。
对于求最小值或者极值这种问题,一般先想到的就是求解微分方程,但是函数很复杂的时候不容易求解,计算机怎么曲线救国呢,通过其擅长的凭借强大计算能力海量尝试,一步步把函数值试出来 ,这个试的过程前人总结了一个法则——Delta法则:它是一种启发式算法,核心思想是使用梯度下降算法寻找最值,让目标收敛到最佳解附近。
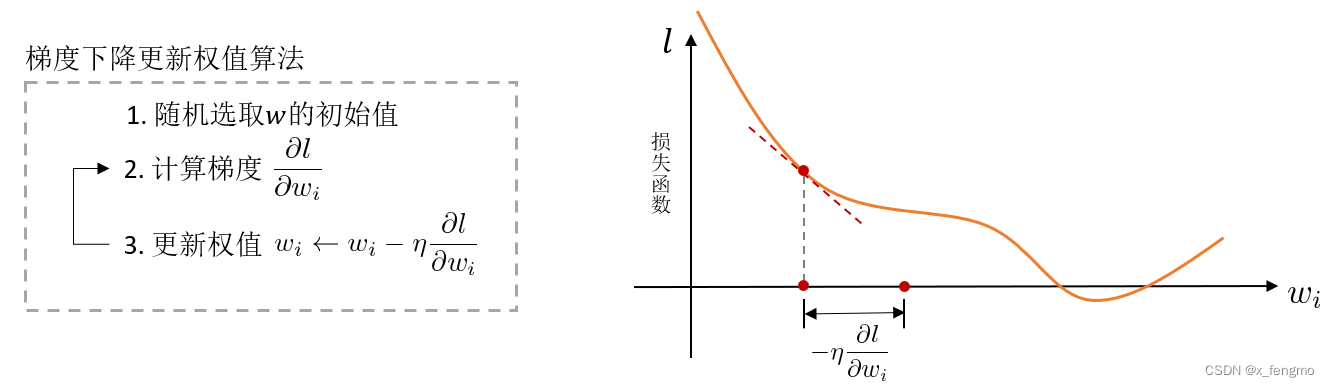
算法的实际做法就是一步步尝试改变权值wi,逐步寻找损失函数l的最小值
问题也来了,为什么偏偏使用∂l∂wi\frac{\partial l}{\partial w_i}∂wi∂l作为一步的步长?其实这个问题也是,对于我们熟悉的梯度grad f=(∂l∂x1,∂l∂x2,…)grad\ f=(\frac{\partial l}{\partial x_1},\frac{\partial l}{\partial x_2},\ldots)grad f=(∂x1∂l,∂x2∂l,…),为什么梯度等于后面这一大串,以至它拥有最大变化率以及其方向的性质
在讨论之前首先要提一下什么是变化率
以一元函数为例y=f(x)y=f(x)y=f(x)
某一段函数的变化率:△y△x=f(x0+△x)−f(x0)△x\frac{\triangle y}{\triangle x} = \frac{f(x_0 + \triangle x) - f(x_0)}{\triangle x}△x△y=△xf(x0+△x)−f(x0)
某一点函数的变化率:lim△x→0f(x0+△x)−f(x0)△x=f′(x0)\lim_{\triangle x\to 0} \frac{f(x_0 + \triangle x) - f(x_0)}{\triangle x} = f'(x_0)lim△x→0△xf(x0+△x)−f(x0)=f′(x0)
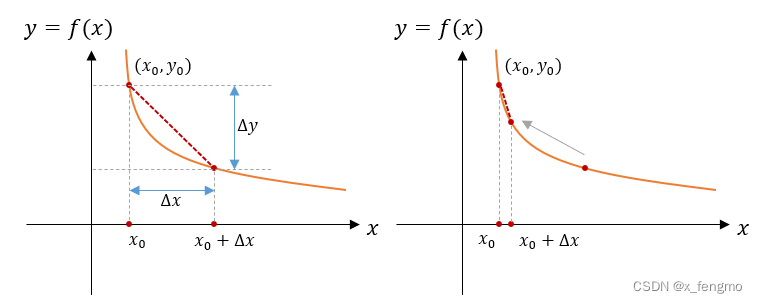
变化率:函数的增量与自变量沿某一方向增量比值的极限(在一元函数里,某一方向也就是x轴方向)
拓展到二元函数z=f(x,y)z=f(x, y)z=f(x,y)
依据上面对变化率的定义中需要自变量的某一方向,此时的方向是由x和y共同影响的,那么先假设这个方向的单位向量为el⃗=(cosα,cosβ)\vec{e_l} = (\cos\alpha, \cos\beta)el=(cosα,cosβ),在这个方向上的增量为t,那么增量向量(自变量)为(tcosα,tcosβ)(t\cos\alpha,t\cos\beta)(tcosα,tcosβ),则变化率=limt→0+f(x0+tcosα,y0+tcosβ)−f(x0,y0)t=fx(x0,y0)cosα+fy(x0,y0)cosβ变化率=\lim_{t \to 0^{+}} \frac{f(x_0 + t\cos\alpha, y_0 + t\cos\beta) - f(x_0, y_0)}{t} = f_x(x_0, y_0)\cos\alpha + f_y(x_0, y_0)\cos\beta 变化率=t→0+limtf(x0+tcosα,y0+tcosβ)−f(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ
推导过程:
当变化率最大时,方向α是怎样的?
将变化率换一种表示方式,看作两向量的内积,其中g⃗=(fx(x0,y0),fy(x0,y0)),el⃗=(cosα,cosβ) \vec{g} = (f_x(x_0, y_0), f_y(x_0, y_0)) , \vec{e_l} = (\cos\alpha, \cos\beta) g=(fx(x0,y0),fy(x0,y0)),el=(cosα,cosβ)
则变化率就变成了limt→0+f(x0+tcosα,y0+tcosβ)−f(x0,y0)t=fx(x0,y0)cosα+fy(x0,y0)cosβ=g⃗⋅el⃗=∣g⃗∣∣el⃗∣cosθ \lim_{t \to 0^{+}} \frac{f(x_0 + t\cos\alpha, y_0 + t\cos\beta) - f(x_0, y_0)}{t} = f_x(x_0, y_0)\cos\alpha + f_y(x_0, y_0)\cos\beta = \vec{g} \cdot \vec{e_l} = \lvert \vec{g} \rvert \lvert \vec{e_l} \rvert \cos \theta t→0+limtf(x0+tcosα,y0+tcosβ)−f(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ=g⋅el=∣g∣∣el∣cosθ
其中θ是∣g⃗∣\lvert \vec{g}\rvert∣g∣和∣el⃗∣\lvert \vec{e_l}\rvert∣el∣的夹角,当已知某一点坐标时,g⃗=(fx(x0,y0),fy(x0,y0))\vec{g} = (f_x(x_0, y_0), f_y(x_0, y_0))g=(fx(x0,y0),fy(x0,y0))值可以确定,即∣g⃗∣\lvert \vec{g}\rvert∣g∣可得为一定值,同时单位向量∣el⃗∣=1\lvert \vec{e_l}\rvert=1∣el∣=1,那么当cosθ=1\cos\theta=1cosθ=1时变化率最大,此时g⃗∥el⃗\vec{g} \parallel \vec{e_l}g∥el
也就是这个方向α是g⃗=(fx(x0,y0),fy(x0,y0))\vec{g} = (f_x(x_0, y_0), f_y(x_0, y_0))g=(fx(x0,y0),fy(x0,y0))方向时,变化率最大
可以向更高维函数推广
对于函数f(a,b,c,…)f(a,b,c,\ldots)f(a,b,c,…),向量(∂f∂a,∂f∂b,∂f∂c,…)(\frac{\partial f}{\partial a}, \frac{\partial f}{\partial b}, \frac{\partial f}{\partial c}, \ldots)(∂a∂f,∂b∂f,∂c∂f,…)就是拥有最大变化率的数值及方向的梯度grad fgrad\ fgrad f
grad f=(∂f∂a,∂f∂b,∂f∂c,…) grad \ f = (\frac{\partial f}{\partial a}, \frac{\partial f}{\partial b}, \frac{\partial f}{\partial c}, \ldots) grad f=(∂a∂f,∂b∂f,∂c∂f,…)
梯度grad fgrad\ fgrad f方向上,函数f(a,b,c,…)f(a,b,c,\ldots)f(a,b,c,…)的数值变化最大
以点(a0,b0,c0,…)(a_0,b_0,c_0,\ldots)(a0,b0,c0,…)为例,在这一点的梯度为(∂f∂a0,∂f∂b0,∂f∂c0,…)(\frac{\partial f}{\partial a_0}, \frac{\partial f}{\partial b_0}, \frac{\partial f}{\partial c_0}, \ldots)(∂a0∂f,∂b0∂f,∂c0∂f,…),也就是由(a0,b0,c0,…)(a_0,b_0,c_0,\ldots)(a0,b0,c0,…)向(a0+t∂f∂a0,b0+t∂f∂b0,c0+t∂f∂c0,…)(a_0 + t\frac{\partial f}{\partial a_0}, b_0 + t\frac{\partial f}{\partial b_0}, c_0 + t\frac{\partial f}{\partial c_0}, \ldots)(a0+t∂a0∂f,b0+t∂b0∂f,c0+t∂c0∂f,…)移动是向函数值f变化幅度最大的方向移动
在梯度下降算法中,对于权值的更新也如同上述例子一样,我们希望找到损失函数l的最小值,因此一步步更新权值wi←wi−η∂l∂wiw_{i}\leftarrow w_{i} - \eta\frac{\partial l}{\partial w_{i}}wi←wi−η∂wi∂l,使用∂l∂wi\frac{\partial l}{\partial w_{i}}∂wi∂l作为一步的步长
梯度中隐含的一些信息
在论文《Soteria: Provable Defense against Privacy Leakage in Federated Learning from Representation Perspective》中作者进一步探究了梯度∂l∂wi\frac{\partial l}{\partial w_{i}}∂wi∂l隐含了哪些信息。隐含的这些信息可能会让窃听者在窃听到梯度信息后,根据梯度还原出原始数据和标签。


若将批的划分等同于类的划分将得到下面的式子

式子(1)与式子(2)的批划分见下图。每一批中进行训练的数据属于同一标签同一类。

作者主要分析的是线性连接层的隐含信息
线性连接层是最后一层
当线性连接层是最后一层时,∂l∂wi\frac{\partial l}{\partial w_{i}}∂wi∂l做进一步拆分

其中,r是这一层的输入,b为输出,y是将b进行归一化后的结果(对y的所有项求和为1),再与真实标签进行异或后生成yc,之后计算出损失函数l
权重W是一个矩阵,求解∂l∂W\frac{\partial l}{\partial W}∂W∂l

W=[W1,W2,…,Wk]W = [W_1, W_2, \ldots, W_k]W=[W1,W2,…,Wk]
W1=[w11,w21,…,wn1]TW_1 = [w_{11}, w_{21}, \ldots, w_{n1}]^TW1=[w11,w21,…,wn1]T
∂l∂w11=∂l∂b1∂b1∂w11=∂l∂b1∂(w11r1+w12r2+…)∂w11=∂l∂b1r1\frac{\partial l}{\partial w_{11}} = \frac{\partial l}{\partial b_1}\frac{\partial b_1}{\partial w_{11}} = \frac{\partial l}{\partial b_1}\frac{\partial (w_{11}r_1 + w_{12}r_2 + \ldots)}{\partial w_{11}} = \frac{\partial l}{\partial b_1}r_1∂w11∂l=∂b1∂l∂w11∂b1=∂b1∂l∂w11∂(w11r1+w12r2+…)=∂b1∂lr1
∂l∂w21=∂l∂b2∂b2∂w21=∂l∂b2∂(w21r1+w22r2+…)∂w21=∂l∂b2r1\frac{\partial l}{\partial w_{21}} = \frac{\partial l}{\partial b_2}\frac{\partial b_2}{\partial w_{21}} = \frac{\partial l}{\partial b_2}\frac{\partial (w_{21}r_1 + w_{22}r_2 + \ldots)}{\partial w_{21}} = \frac{\partial l}{\partial b_2}r_1∂w21∂l=∂b2∂l∂w21∂b2=∂b2∂l∂w21∂(w21r1+w22r2+…)=∂b2∂lr1
⋮\ \ \ \ \vdots ⋮
∂l∂wn1=∂l∂bn∂bn∂wn1=∂l∂bnr1\frac{\partial l}{\partial w_{n1}} = \frac{\partial l}{\partial b_n}\frac{\partial b_n}{\partial w_{n1}} = \frac{\partial l}{\partial b_n}r_1∂wn1∂l=∂bn∂l∂wn1∂bn=∂bn∂lr1
整合之后
∂l∂W1=[∂l∂b1r1∂l∂b2r1⋮∂l∂bnr1]=[∂l∂b1∂l∂b2⋮∂l∂bn]r1 \frac{\partial l}{\partial W_1} = \begin{bmatrix}
\frac{\partial l}{\partial b_1}r_1 \\
\frac{\partial l}{\partial b_2}r_1 \\
\vdots \\
\frac{\partial l}{\partial b_n}r_1
\end{bmatrix} = \begin{bmatrix}
\frac{\partial l}{\partial b_1} \\
\frac{\partial l}{\partial b_2} \\
\vdots \\
\frac{\partial l}{\partial b_n}
\end{bmatrix}r_1
∂W1∂l=∂b1∂lr1∂b2∂lr1⋮∂bn∂lr1=∂b1∂l∂b2∂l⋮∂bn∂lr1
推广到任意行向量
∂l∂Wi=[∂l∂b1ri∂l∂b2ri⋮∂l∂bnri]=[∂l∂b1∂l∂b2⋮∂l∂bn]ri=∂l∂bri
\frac{\partial l}{\partial W_i} = \begin{bmatrix}
\frac{\partial l}{\partial b_1}r_i \\
\frac{\partial l}{\partial b_2}r_i \\
\vdots \\
\frac{\partial l}{\partial b_n}r_i
\end{bmatrix} = \begin{bmatrix}
\frac{\partial l}{\partial b_1} \\
\frac{\partial l}{\partial b_2} \\
\vdots \\
\frac{\partial l}{\partial b_n}
\end{bmatrix}r_i = \frac{\partial l}{\partial \mathbf{b}}r_i
∂Wi∂l=∂b1∂lri∂b2∂lri⋮∂bn∂lri=∂b1∂l∂b2∂l⋮∂bn∂lri=∂b∂lri
再将行向量整合成矩阵得到如下式子
∂l∂W=[∂l∂W1,∂l∂W2,…,∂l∂Wk]=[∂l∂b1∂l∂b2⋮∂l∂bn][r1,r2,…,rk]=∂l∂b(r)T
\frac{\partial l}{\partial W} = \begin{bmatrix}
\frac{\partial l}{\partial W_1}, \frac{\partial l}{\partial W_2},\ldots,\frac{\partial l}{\partial W_k}
\end{bmatrix} = \begin{bmatrix}
\frac{\partial l}{\partial b_1} \\
\frac{\partial l}{\partial b_2} \\
\vdots \\
\frac{\partial l}{\partial b_n}
\end{bmatrix}\begin{bmatrix}
r_1,r_2,\ldots,r_k
\end{bmatrix} = \frac{\partial l}{\partial \mathbf{b}}(\mathbf{r})^T
∂W∂l=[∂W1∂l,∂W2∂l,…,∂Wk∂l]=∂b1∂l∂b2∂l⋮∂bn∂l[r1,r2,…,rk]=∂b∂l(r)T
如果损失函数l使用交叉熵loss函数(类别为c时):lossc=−logebc∑k=1nebkloss_c = - \log\frac{e^{b_c}}{\sum_{k=1}^{n}e^{b_k}}lossc=−log∑k=1nebkebc
那么上式中的∂l∂b\frac{\partial l}{\partial \mathbf{b}}∂b∂l就可以尝试去表示
当数据的标签为class c时,
∂lc∂b1=∂(−logebceb1+…+ebc+…+ebn)∂b1=∂(−logebc+log(eb1+…+ebc+…+ebn))∂b1=eb1eb1+…+ebc+…+ebn=y1 \begin{align}
\frac{\partial l_c}{\partial b_1} &= \frac{\partial (- \log \frac{e^{b_c}}{e^{b_1} + \ldots + e^{b_c} + \ldots + e^{b_n}})}{\partial b_1} = \frac{\partial ( - \log e^{b_c} + \log (e^{b_1} + \ldots + e^{b_c} + \ldots + e^{b_n}))}{\partial b_1} \nonumber \\
&= \frac{e^{b_1}}{e^{b_1} + \ldots + e^{b_c} + \ldots + e^{b_n}} = y_1 \nonumber
\end{align} ∂b1∂lc=∂b1∂(−logeb1+…+ebc+…+ebnebc)=∂b1∂(−logebc+log(eb1+…+ebc+…+ebn))=eb1+…+ebc+…+ebneb1=y1
∂lc∂bc=∂(−logebceb1+…+ebc+…+ebn)∂bc=∂(−logebc+log(eb1+…+ebc+…+ebn))∂bc=−1+ebceb1+…+ebc+…+ebn=yc−1 \begin{align}
\frac{\partial l_c}{\partial b_c} &= \frac{\partial (- \log \frac{e^{b_c}}{e^{b_1} + \ldots + e^{b_c} + \ldots + e^{b_n}})}{\partial b_c} = \frac{\partial ( - \log e^{b_c} + \log (e^{b_1} + \ldots + e^{b_c} + \ldots + e^{b_n}))}{\partial b_c} \nonumber \\
&= -1 + \frac{e^{b_c}}{e^{b_1} + \ldots + e^{b_c} + \ldots + e^{b_n}} = y_c - 1 \nonumber
\end{align} ∂bc∂lc=∂bc∂(−logeb1+…+ebc+…+ebnebc)=∂bc∂(−logebc+log(eb1+…+ebc+…+ebn))=−1+eb1+…+ebc+…+ebnebc=yc−1
∂lc∂b=[∂lc∂b1⋮∂lc∂bc⋮∂lc∂bn]=[y1⋮yc−1⋮yn]
% code
\frac{\partial l_c}{\partial \mathbf{b}} = \begin{bmatrix}
\frac{\partial l_c}{\partial b_1} \\
\vdots \\
\frac{\partial l_c}{\partial b_c}\\
\vdots \\
\frac{\partial l_c}{\partial b_n} \end{bmatrix} = \begin{bmatrix}
y_1 \\
\vdots \\
y_c - 1 \\
\vdots \\
y_n \end{bmatrix}
∂b∂lc=∂b1∂lc⋮∂bc∂lc⋮∂bn∂lc=y1⋮yc−1⋮yn
并且存在关系式∣yc−1∣=∣y1∣+…+∣yc−1∣+∣yc+1∣+…|y_c - 1| = |y_1| + \ldots + |y_{c-1}| + |y_{c+1}| + \ldots∣yc−1∣=∣y1∣+…+∣yc−1∣+∣yc+1∣+…
因为∑iyi=1\sum_{i} y_i = 1∑iyi=1
通过观察∂lc∂b\frac{\partial l_c}{\partial \mathbf{b}}∂b∂lc可以发现,当训练数据为c时,第c行的幅度最大,在所有行都乘以一个相同的行向量(r)T(\mathbf{r})^T(r)T时,∂l∂Wi=∂l∂b(r)T\frac{\partial l}{\partial W_i} = \frac{\partial l}{\partial \mathbf{b}}(\mathbf{r})^T∂Wi∂l=∂b∂l(r)T这一行的幅度依旧最大。那么攻击者窃听到梯度信息后,找到幅度最大的一行,这一行就是(yc−1)(r)T(y_c - 1)(\mathbf{r})^T(yc−1)(r)T,其中(yc−1)(y_c - 1)(yc−1)是一个常数,(yc−1)(r)T(y_c - 1)(\mathbf{r})^T(yc−1)(r)T近似可看为(r)T(\mathbf{r})^T(r)T。这样就得到了这一层的输入r\mathbf{r}r。
结论:通过梯度∇W\nabla W∇W可以得到本层的输入数据r\mathbf{r}r,并且还知道这个数据所属的类别class c。
线性层作为中间层
线性层作为中间层时,会进行下面这样的数据变换

简化一下就是下面这种表达

这其中的激活函数σ\sigmaσ扮演了非常重要的角色,其主要作用是对所有的隐藏层和输出层添加一个非线性的操作
以一个三层全线性连接的神经网络为例

z1=W1x+B1z2=W2σ(z1)+B2z3=W3σ(z2)+B3
\begin{align}
& z_1 = W_1x + B_1 \nonumber \\
& z_2 = W_2\sigma(z_1) + B_2 \nonumber \\
& z_3 = W_3\sigma(z_2) + B_3 \nonumber
\end{align}
z1=W1x+B1z2=W2σ(z1)+B2z3=W3σ(z2)+B3
则所有∂l∂Wi\frac{\partial l}{\partial W_i}∂Wi∂l可表达
这里的Wi和之前的不一样,之前的指一个权重矩阵的一列,是一个向量,这里代表第几层的权重,是一个矩阵
∂l∂W1=∂l∂z3∂z3∂W1=∂l∂z3(∂(W3σ(z2)+B3)∂σ(z2)∂σ(z2)∂z2∂(W2σ(z1)+B2)∂σ(z1)∂σ(z1)∂z1∂(W1x+B1)∂W1)=∂l∂z3(W3⋅σ′(z2)⋅W2⋅σ′(z1)⋅x)∂l∂W2=∂l∂z3∂z3∂W2=∂l∂z3(∂(W3σ(z2)+B3)∂σ(z2)∂σ(z2)∂z2∂(W2σ(z1)+B2)∂W2)=∂l∂z3(W3⋅σ′(z2)⋅σ(z1))∂l∂W3=∂l∂z3∂z3∂W3=∂l∂z3∂(W3σ(z2)+B3)∂W3=∂l∂z3σ(z2)
\begin{align}
& \frac{\partial l}{\partial W_1} = \frac{\partial l}{\partial z_3} \frac{\partial z_3}{\partial W_1} = \frac{\partial l}{\partial z_3}(\frac{\partial(W_3\sigma(z_2) + B_3)}{\partial \sigma(z_2)} \frac{\partial \sigma(z_2)}{\partial z_2} \frac{\partial(W_2\sigma(z_1) + B_2)}{\partial \sigma(z_1)} \frac{\partial \sigma(z_1)}{\partial z_1} \frac{\partial(W_1x + B_1)}{\partial W_1}) = \frac{\partial l}{\partial z_3}(W_3 \cdot \sigma'(z_2) \cdot W_2 \cdot \sigma'(z_1) \cdot x) \nonumber \\
& \frac{\partial l}{\partial W_2} = \frac{\partial l}{\partial z_3} \frac{\partial z_3}{\partial W_2} = \frac{\partial l}{\partial z_3}(\frac{\partial(W_3\sigma(z_2) + B_3)}{\partial \sigma(z_2)} \frac{\partial \sigma(z_2)}{\partial z_2} \frac{\partial (W_2\sigma(z_1) + B_2)}{\partial W_2}) = \frac{\partial l}{\partial z_3}(W_3 \cdot \sigma'(z_2) \cdot \sigma(z_1)) \nonumber \\
& \frac{\partial l}{\partial W_3} = \frac{\partial l}{\partial z_3}\frac{\partial z_3}{\partial W_3} = \frac{\partial l}{\partial z_3} \frac{\partial(W_3\sigma(z_2) + B_3)}{\partial W_3} = \frac{\partial l}{\partial z_3}\sigma(z_2) \nonumber
\end{align}
∂W1∂l=∂z3∂l∂W1∂z3=∂z3∂l(∂σ(z2)∂(W3σ(z2)+B3)∂z2∂σ(z2)∂σ(z1)∂(W2σ(z1)+B2)∂z1∂σ(z1)∂W1∂(W1x+B1))=∂z3∂l(W3⋅σ′(z2)⋅W2⋅σ′(z1)⋅x)∂W2∂l=∂z3∂l∂W2∂z3=∂z3∂l(∂σ(z2)∂(W3σ(z2)+B3)∂z2∂σ(z2)∂W2∂(W2σ(z1)+B2))=∂z3∂l(W3⋅σ′(z2)⋅σ(z1))∂W3∂l=∂z3∂l∂W3∂z3=∂z3∂l∂W3∂(W3σ(z2)+B3)=∂z3∂lσ(z2)
整理一下
∂l∂W3=∂l∂z3σ(z2)∂l∂W2=∂l∂z3(W3⋅σ′(z2)⋅σ(z1))=∂l∂z3(∂z3∂z2′⋅σ′(z2)⋅σ(z1))∂l∂W1=∂l∂z3(W3⋅σ′(z2)⋅W2⋅σ′(z1)⋅x)=∂l∂z3(∂z3∂z2′⋅σ′(z2)⋅∂z2∂z1′⋅σ′(z1)⋅x)
\begin{align}
& \frac{\partial l}{\partial W_3} = \frac{\partial l}{\partial z_3}\sigma(z_2) \nonumber \\
& \frac{\partial l}{\partial W_2} = \frac{\partial l}{\partial z_3}(W_3 \cdot \sigma'(z_2) \cdot \sigma(z_1)) = \frac{\partial l}{\partial z_3}(\frac{\partial z_3}{\partial z'_2} \cdot \sigma'(z_2) \cdot \sigma(z_1)) \nonumber \\
& \frac{\partial l}{\partial W_1} = \frac{\partial l}{\partial z_3}(W_3 \cdot \sigma'(z_2) \cdot W_2 \cdot \sigma'(z_1) \cdot x) = \frac{\partial l}{\partial z_3}(\frac{\partial z_3}{\partial z'_2} \cdot \sigma'(z_2) \cdot \frac{\partial z_2}{\partial z'_1} \cdot \sigma'(z_1) \cdot x) \nonumber
\end{align}
∂W3∂l=∂z3∂lσ(z2)∂W2∂l=∂z3∂l(W3⋅σ′(z2)⋅σ(z1))=∂z3∂l(∂z2′∂z3⋅σ′(z2)⋅σ(z1))∂W1∂l=∂z3∂l(W3⋅σ′(z2)⋅W2⋅σ′(z1)⋅x)=∂z3∂l(∂z2′∂z3⋅σ′(z2)⋅∂z1′∂z2⋅σ′(z1)⋅x)
如果一个等式其他项都已知,只有一项不知,则这一项是可求的

蓝色为已知,红色为可求,上式可逐步求出神经网络的输入数据x
因为大部分激活函数有相似的结构和稀疏性,所以论文在推导的时候,使用z去近似z’
因此攻击者在窃听到梯度信息之后,通过计算还原出原始训练数据是很有可能的,因此需要针对这种情况对训练数据或者中间训练过程进行一定情况的扰动,以达到安全保护原始数据的目的。




 文章探讨了梯度在多维函数极值寻找中的作用,特别是在深度学习中用于优化损失函数的梯度下降算法。通过分析梯度的性质,解释了为何使用梯度的偏导数作为权值更新的步长。同时,文章指出在深度学习的线性层中,梯度信息可能隐含原始输入数据的细节,这可能导致隐私泄露问题,特别是在使用交叉熵损失函数时。因此,理解并保护梯度信息的安全性对于防止隐私侵犯至关重要。
文章探讨了梯度在多维函数极值寻找中的作用,特别是在深度学习中用于优化损失函数的梯度下降算法。通过分析梯度的性质,解释了为何使用梯度的偏导数作为权值更新的步长。同时,文章指出在深度学习的线性层中,梯度信息可能隐含原始输入数据的细节,这可能导致隐私泄露问题,特别是在使用交叉熵损失函数时。因此,理解并保护梯度信息的安全性对于防止隐私侵犯至关重要。
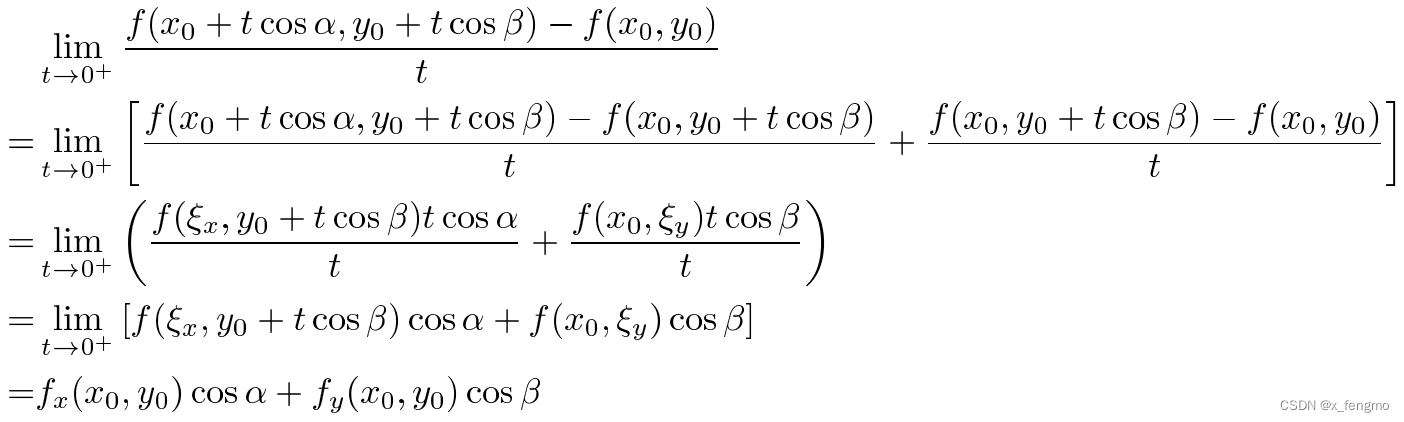


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










