红黑树的变色与旋转

        红黑树是自平衡的二叉查找树，所以了解红黑树之前我们需要先了解什么是二叉查找树。

 

二叉查找树

 

     1.某节点的左子树节点值仅包含小于该节点的值

     2.某节点的右子树节点值仅包含大于该节点的值

     3.左右子树也必须是二叉查找树

 

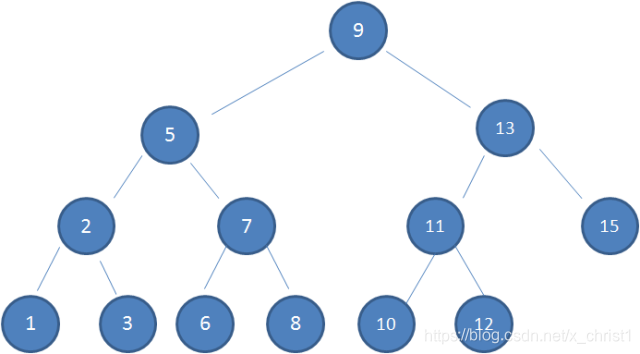
          这样的数据结构的好处就在于，当我查询10这个节点时，10>9,查看右孩子13，10<13,查看左孩子11，10<11，查看左孩子10，发现10正是要查找的节点，大大提交查询效率，这种方式是二分查找的思想，查询所需的最大次数等同于二叉查找树的高度。

 

二叉查找树的局限性

 

      当我们插入7，6，5，4，3时，我们会发现树结构是这样的。

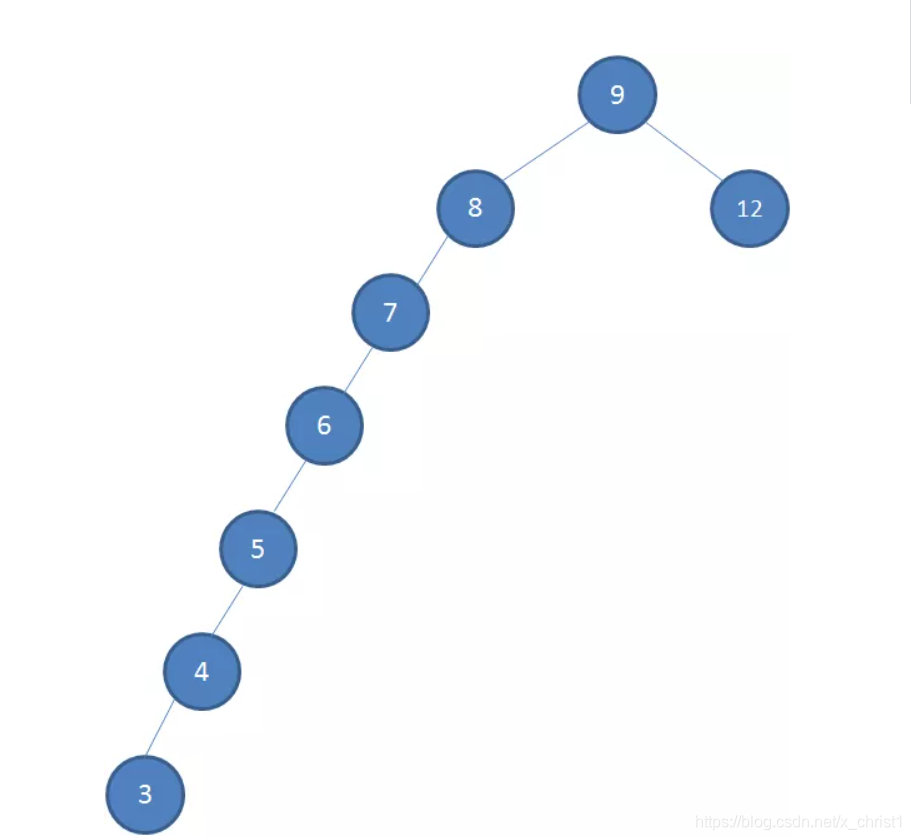
         这样我们会发现也符合二叉树的结构，但是这样线性的结构会导致我们的查找性能大打折扣，所以我们需要解决二叉树多次插入新节点而导致的不平衡，红黑树就出现了。

 

红黑树

 

     红黑树是自平衡的二叉树，除了满足二叉树的特性外，还应具备以下特性:

      1.每个节点只有黑红两色

      2.树的根节点是黑色的

      3.没有两个相邻的红色节点，即一个红色节点它的父节点和子结点中不能存在红色节点

      4.从节点(包括根节点)到其任何后代的NULL节点(每个叶子节点下面有两个空节点)的路径上黑色节点的数量是相同的

 

     当我们插入新节点时，新节点是红色的，应为黑色节点会导致第4条规则更难去调节子树。当新节点的父节点是黑色时，就不需要去变化了，但是当是红色时，我们需要对其进行处理。

主要两大操作:

     1.recolor(变色)

     2.rotation(旋转)

 

      假设我们新插入节点为X

       1.将新插入的节点标记为红色

       2.如果x是根节点，则标记为黑色

       3.如果x的parent不是黑色，同时x也不是root

       x的uncle(叔叔)颜色不同，操作也分为两种情况

 

(1) 变色

 

        如果x的uncle(叔叔)是红色

•   将x的parent和uncle标记为黑色
•   将x的祖父标记为红色
•  让x颜色与x祖父的颜色相同，然后重复不走2，3直到符合红黑树的特性       

 

            

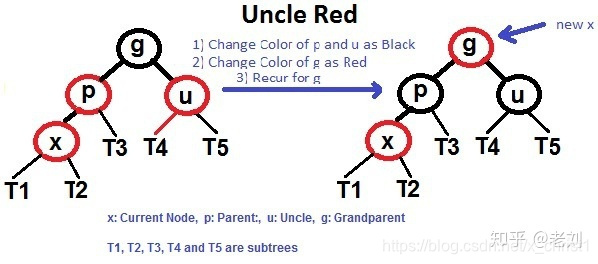
        跟着上面的公式走：

1.  将新插入的x节点标记为红色
2. 发现x的父节点p是红色，违反了红黑树的第3条特性
3. 发现x的uncleu同样是红色
4. 将p和u标记为黑色
5. 将x的祖父标记为红色，此时g就是新的x，继续重复2和3的步骤
6. 发现g是根节点，标记为黑色，结束

 

（2）旋转

 

        如果x的叔叔是黑色，要考虑四种情况，左左，左右，右左，右右，主要演示旋转，第4条特性先忽略。

      

        左左

        这种情况很简单，想象这是一根绳子，手提起 P 节点，然后变色即可

 

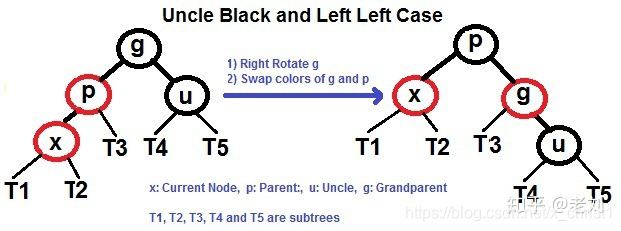
        左右

        左旋: 使 X 的父节点 P 被 X 取代，同时父节点 P 成为 X 的左孩子，然后再应用 左左情况

 

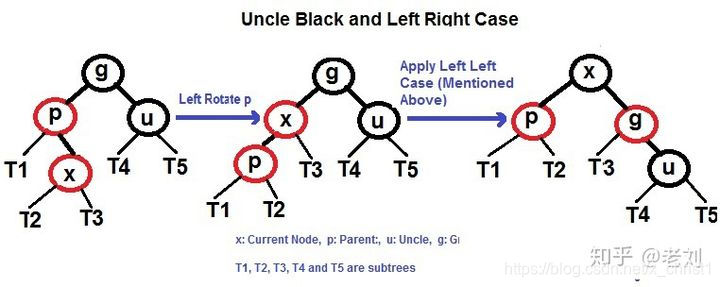
        右左

        右旋: 使 X 的父节点 P 被 X 取代，同时父节点 P 成为 X 的右孩子，然后再应用 右右情况

     

 

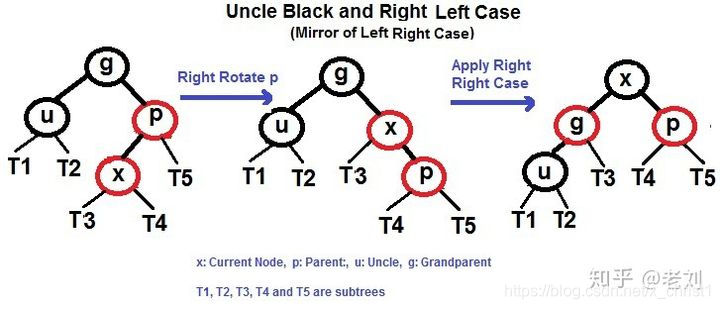
       右右

         与左左情况一样，想象成一根绳子

 

 

 

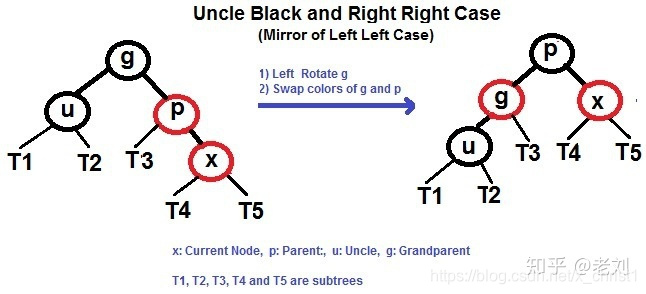
案例:

     在一个二叉树插入节点21：

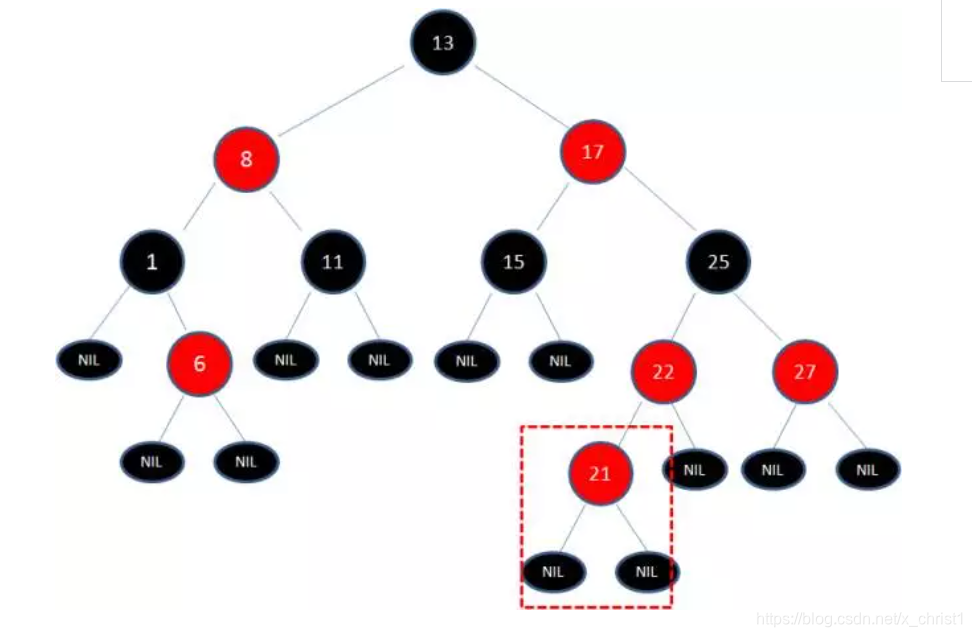
首先，我们需要做的是变色，把节点25及其下方的节点变色：

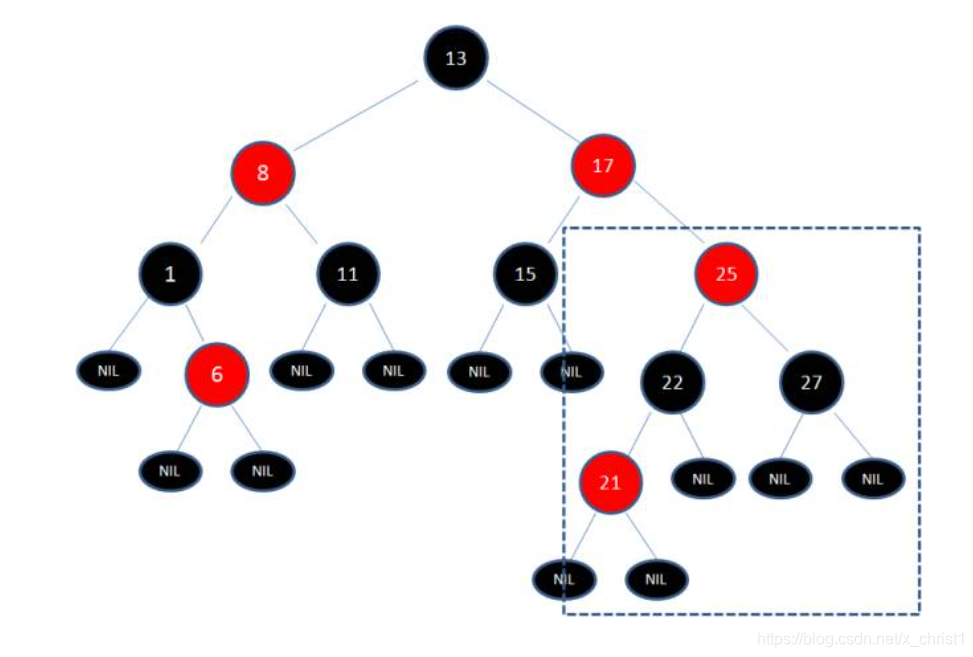
此时节点17和节点25是连续的两个红色节点，那么把节点17变成黑色节点？恐怕不合适。这样一来不但打破了规则4，而且根据规则2（根节点是黑色），也不可能把节点13变成红色节点。 变色已无法解决问题，我们可以用到旋转。

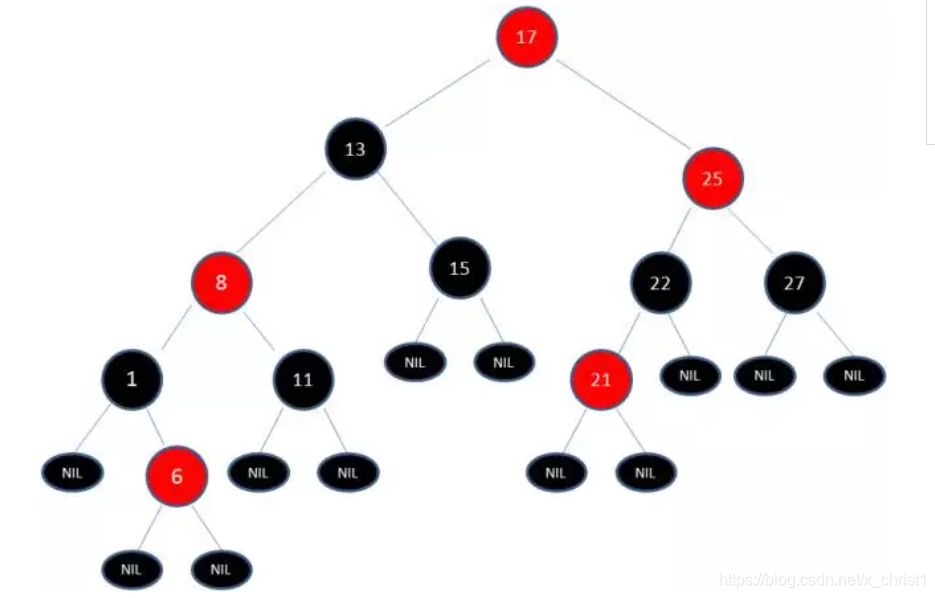
由于根节点必须是黑色节点，所以需要变色，变色结果如下：

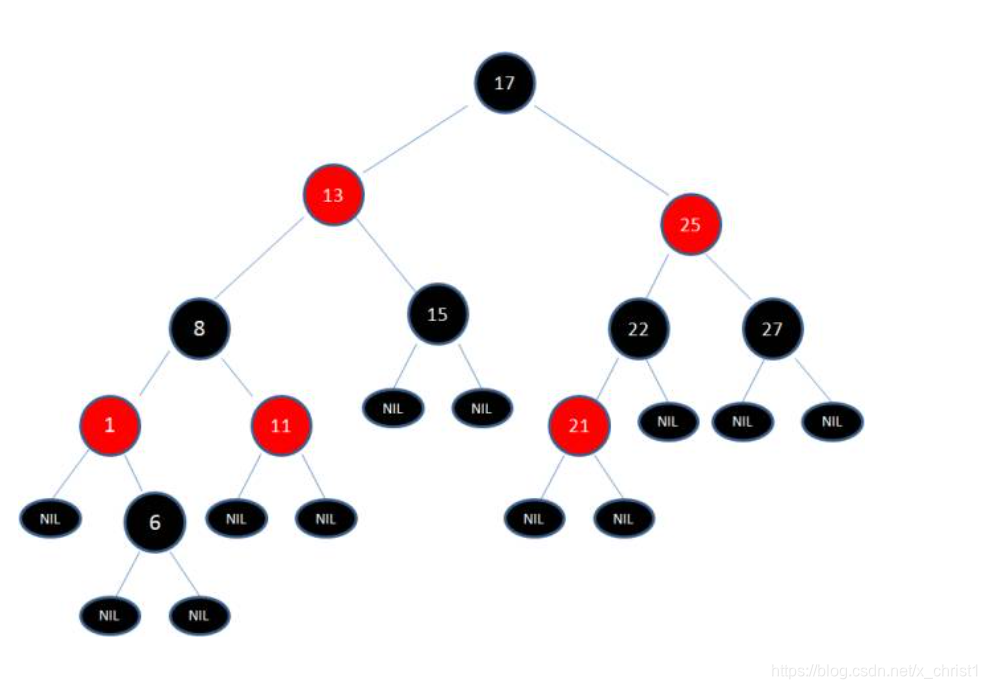
这样就结束了吗？并没有。因为其中两条路径(17 -> 8 -> 6 -> NIL)的黑色节点个数是4，其他路径的黑色节点个数是3，不符合规则5。

 

这时候我们需要把节点13看做X，节点8看做Y，像刚才的示意图那样进行右旋转

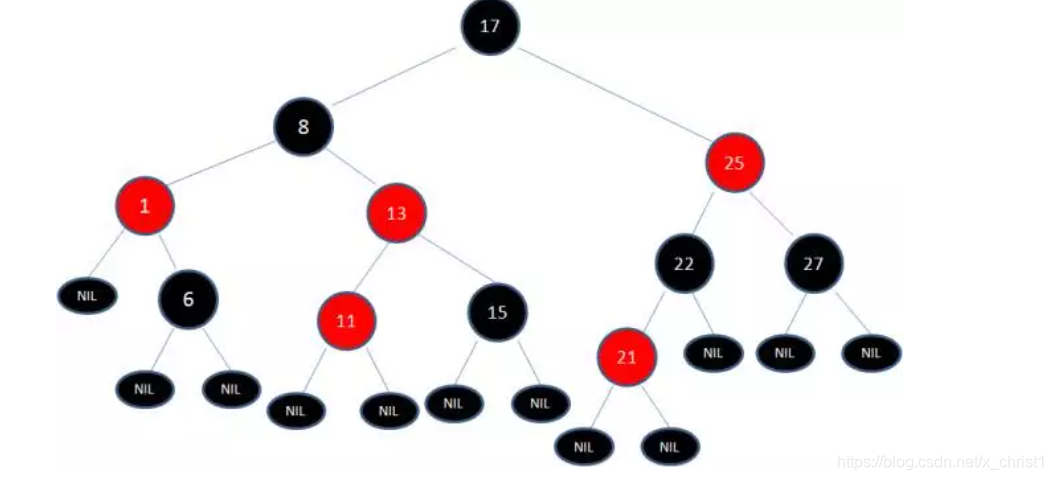
最后根据规则来进行 变色 ：

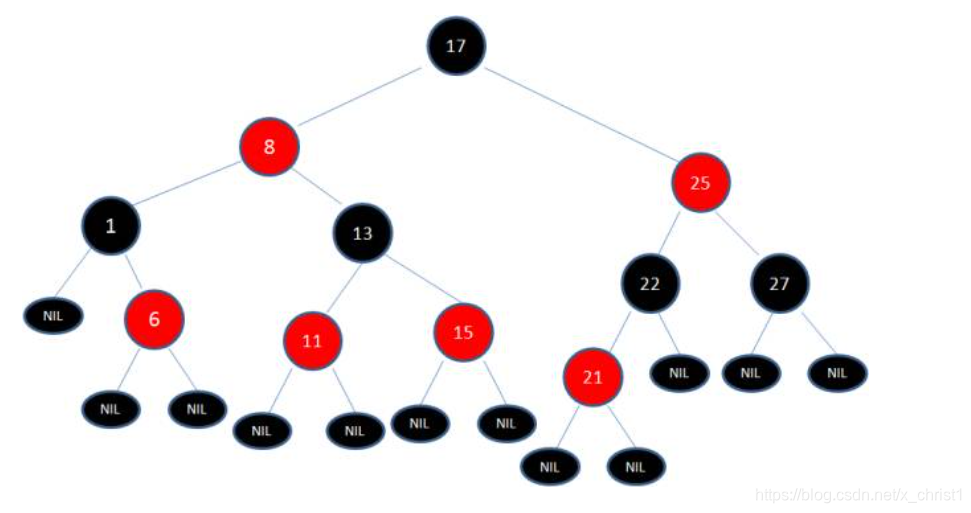
如此一来，我们的红黑树变得重新符合规则。这一个例子的调整过程比较复杂，经历了如下步骤：

 

变色 -> 左旋转 -> 变色 -> 右旋转 -> 变色

 

 

红黑树生成工具: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html