霍夫曼编码（贪心算法）

原创已于 2025-11-22 11:11:44 修改 · 588 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#贪心算法 #算法

于 2025-11-22 00:45:17 首次发布

霍夫曼编码（贪心算法）

1.背景
2.图说原理
3.代码实现霍夫曼编码(AI 写的)
4.优化

1.背景

最近看到一个贪心算法的概念，比较多的举例是用各种面额的钞票给人快速找零；突然一个霍夫曼编码的名词出现，也是用贪心算法，有什么用呢，问 ai 说是一种压缩的概念，勾起了我的好奇心，这是干啥的，怎么实现的。

2.图说原理

在这里插入图片描述

2.1 为啥要编码

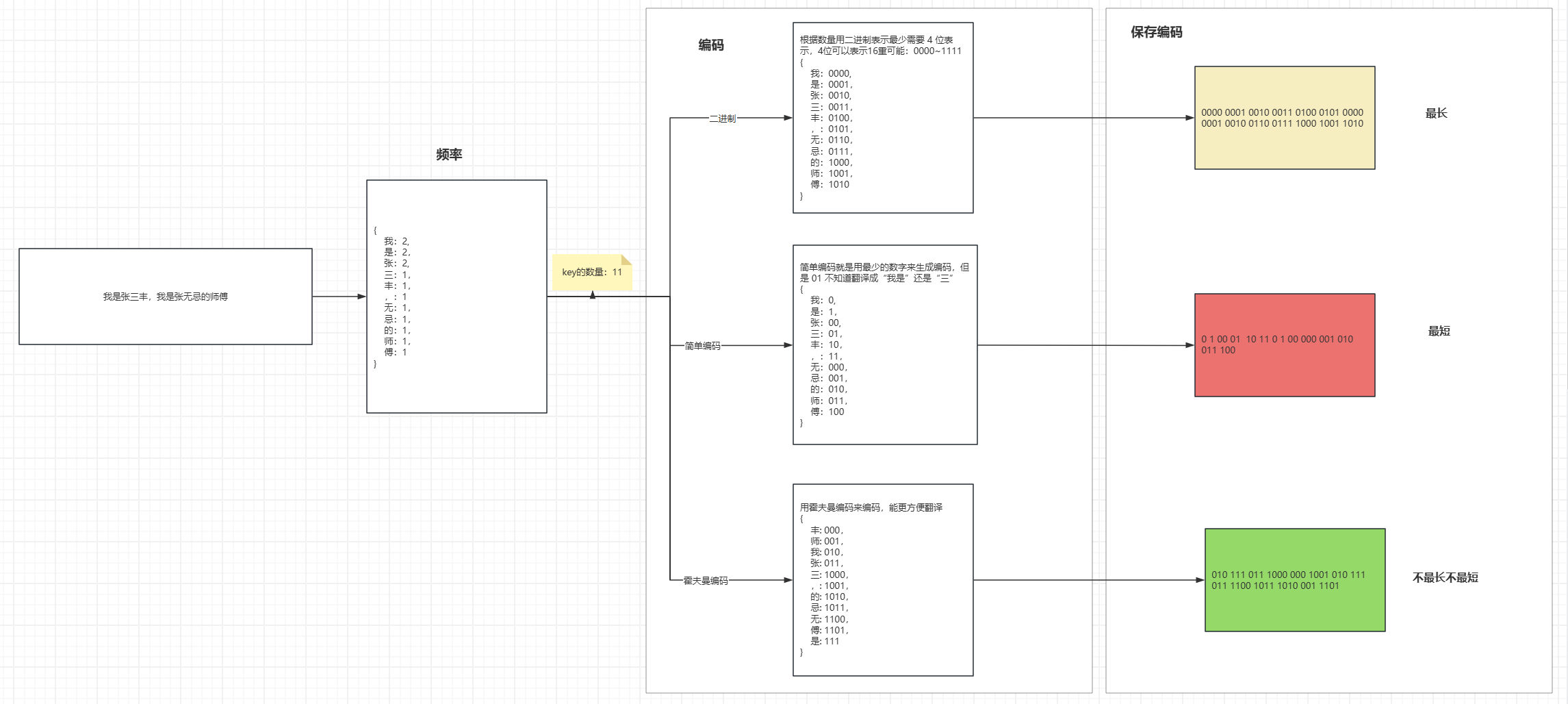
首先算出频率，就是每个字出现的次数，然后编码成 0101011010100... 类似这样的格式，为什么呢，因为 01可以按位存储，正常的一个字符比如采用utf8mb4是4个字节，一个字节是8位，那么一个字符就占用32 位了，裸眼计算明显按位存储更优；如上图所示，但是长度、可行性不一样

2.2 二进制编码

去重后的数量来计算二进制位数，比如 3 个字，那么用 2 位（4种可能）表示，7 个字用 3 位（8种可能）表示，12 位用 4 位（16种可能）；每一个字符都有固定的长度和唯一的编码；可以对存储的编码进行解码，但是最长

2.3 简单编码

直接用最短的位数开始排，这样最少的位数能表示最多的编码；明显最短，但是解码是一个头疼的问题。对应 01怎么区分是“0我1是两个字”，还是“01一个字三”，别看我图上有空格，但是真正按位存储的时候是没有空格的。

2.4 霍夫曼编码

使用霍夫曼编码生成的编码，每一个字的对应的前缀是唯一的，没有像第二种那样重复的情况，直接从头匹配，找到了就翻译，去掉翻译完的位，接着往下找就可以了；不最长不最短，但是能解码；解码时候比第一种固定长度的麻烦，但是是可以实现的，压缩嘛，压缩率的权重可以看的更高撒；（个人不成熟认为固定长度编码方便并发解码，毕竟可以等位分割起线程；让我来搞霍夫曼编码可能会加入特殊的字节用来分割它，分割后进行并发处理；有点飘了，实际的压缩算法看 AI 介绍比单纯一种算法更麻烦，会对霍夫曼编码优化或者变形，不想深入了）

3.代码实现霍夫曼编码(AI 写的)

import heapq


class Node:
    def __init__(self, char, freq):
        self.char = char
        self.freq = freq
        self.left = None
        self.right = None

    def __lt__(self, other):
        return self.freq < other.freq


def build_huffman_tree(chars, freqs):
    """构建霍夫曼树"""
    heap = []
    for char, freq in zip(chars, freqs):
        heapq.heappush(heap, Node(char, freq))

    while len(heap) > 1:
        left = heapq.heappop(heap)
        right = heapq.heappop(heap)

        merged = Node(None, left.freq + right.freq)
        merged.left = left
        merged.right = right

        heapq.heappush(heap, merged)

    return heap[0]


def generate_codes(node, current_code, codes):
    """生成霍夫曼编码"""
    if node is None:
        return

    if node.char is not None:
        codes[node.char] = current_code
        return

    generate_codes(node.left, current_code + "0", codes)
    generate_codes(node.right, current_code + "1", codes)


def huffman_coding(chars, freqs):
    """霍夫曼编码主函数"""
    root = build_huffman_tree(chars, freqs)
    print('root',root)
    codes = {}
    generate_codes(root, "", codes)
    return codes


# 测试
chars = ['我', '是', '张', '三', '丰','，','无','忌','的','师','傅']
freqs = [2,2,2,1,1,1,1,1,1,1,1]
huffman_codes = huffman_coding(chars, freqs)
print("霍夫曼编码:")
for char, code in huffman_codes.items():
    print(f"{char}: {code}")

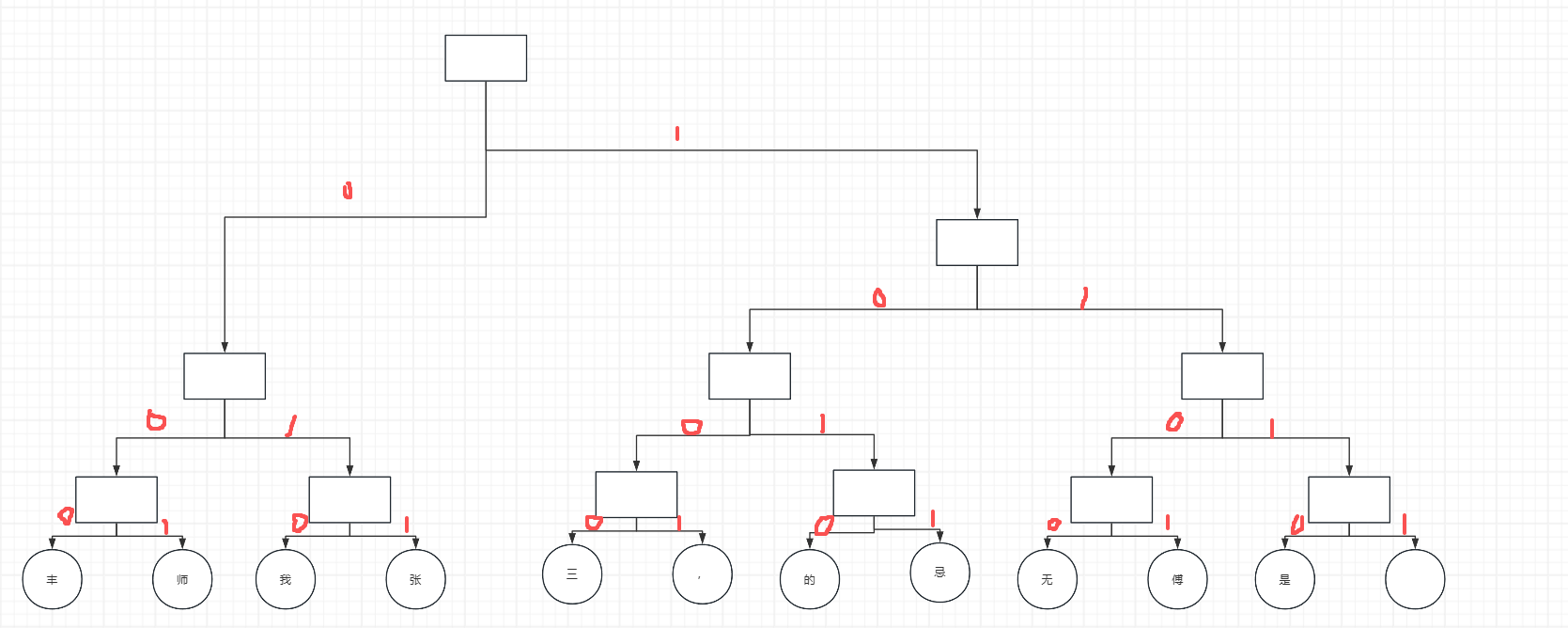
算法就是先生成一颗二叉树，然后对这棵树从树根到叶子编码，左0右1.树结构如下：

4.优化

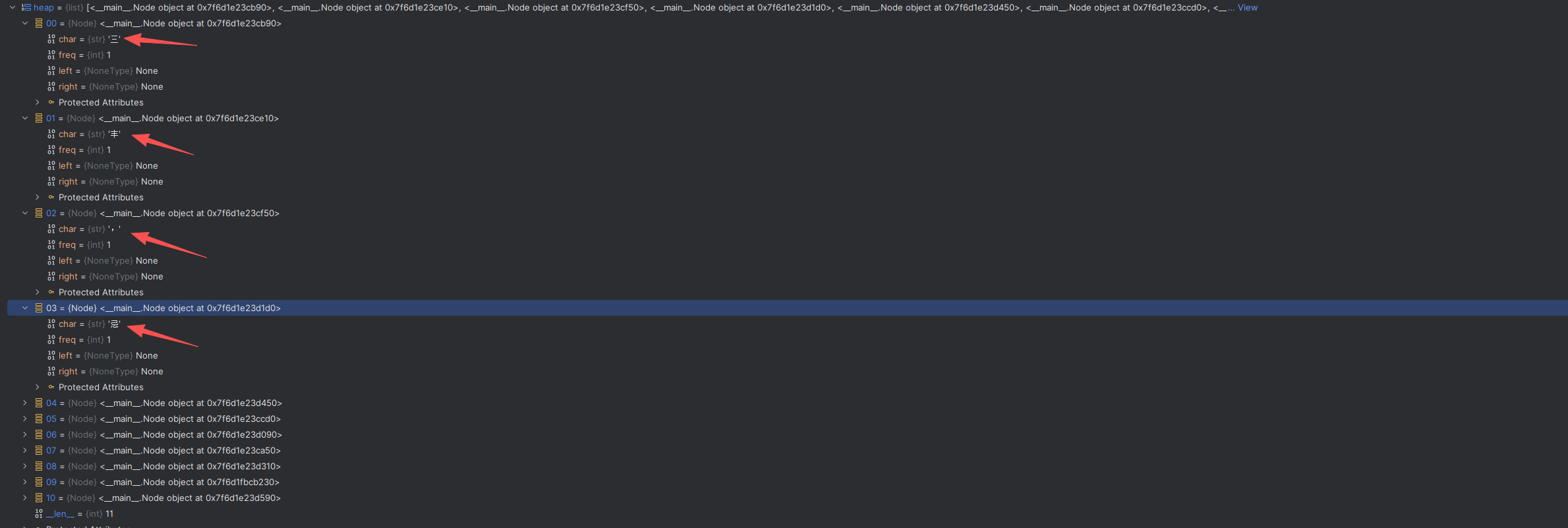
上面的图在执行的时候使用 python 的 heap 进行插入的时候，heap 并没有按照插入顺序保存，这可能是 heap 的什么机制吧，如下图
还有一个优化的点，就是先把频率按照词频的正序排列后再编码，因为根据算法越到后面入队的话，生成的编码相对较短，越短的位来存储较高频率的字符，占用的空间就越少。
最后给霍夫曼点个 6