本文总结了动态规划中的状态压缩技术，包括1维、2维和3维dp的压缩方法，通过实例分析198. 打家劫舍、416. 分割等和子集、10. 正则表达式匹配和188. 买卖股票的最佳时机 IV等问题，阐述如何通过状态转移方程优化存储空间，提高算法效率。
题目
198. 打家劫舍，1维dp压缩到0维
198. 打家劫舍
状态压缩前的代码如下：
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[length - 1];
i-2, i-1, i
dp1,dp2
计算dp[i]只需要前两个状态dp[i-1]和dp[i-2]，所以数组dp[]可以压缩为2个数dp1和dp2。更新前dp1=dp[i-2], dp2=dp[i-1], 更新后下标都加1，变成dp1=dp[i-1], dp2=dp[i]。
int dp1=nums[0];
int dp2=Math.max(nums[0], nums[1]);;
for(int i = 2; i < length; i++){
int tmp=dp2;//保存dp[i-1]
dp2=Math.max(dp1+nums[i],dp2);//左边为更新后的，右边为更新前的
dp1=tmp;
}
return dp2;//dp2指向最后一个
416. 分割等和子集，2维dp压缩为1维
416. 分割等和子集
状态压缩前，代码如下：
boolean[][] dp = new boolean[n][target + 1];
for (int i = 0; i < n; i++) {
dp[i][0] = true;
}
dp[0][nums[0]] = true;
for (int i = 1; i < n; i++) {
int num = nums[i];
for (int j = 1; j <= target; j++) {
if (j >= num) {
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[n - 1][target];
根据状态转移方程dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num]，计算dp[i][j]只用到了第i-1行结果，所以可以将二维dp[i][j]压缩为1为dp[j]。更新dp[j]需要上一行的dp[j-num]，所以需要逆向更新dp[j]，保证结果正确。
状态压缩后的代码如下：
// boolean[][] dp = new boolean[n][target + 1];
boolean[] dp=new boolean[target + 1];//压缩为一维dp
// for (int i = 0; i < n; i++) {
// dp[i][0] = true;
// }
// dp[0][nums[0]] = true;
dp[0]=true;
dp[nums[0]]=true;
for (int i = 1; i < n; i++) {
int num = nums[i];
// for (int j = 1; j <= target; j++) {
// if (j >= num) {
// dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
// } else {
// dp[i][j] = dp[i - 1][j];
// }
// }
for(int j=target;j>=num;j--){//压缩为一维dp后，需要逆向遍历
dp[j]=dp[j] || dp[j-num];
}
}
// return dp[n - 1][target];
return dp[target];
10. 正则表达式匹配，2维dp压缩到1维
10. 正则表达式匹配
状态压缩的完整代码见动态规划+状态压缩。
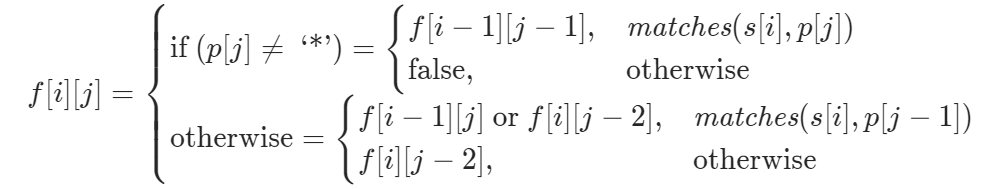
状态压缩前的代码如下：
boolean[][] f = new boolean[m + 1][n + 1];
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p.charAt(j - 1) == '*') {
f[i][j] = f[i][j - 2];
if (matches(s, p, i, j - 1)) {
f[i][j] = f[i][j] || f[i - 1][j];
}
} else {
if (matches(s, p, i, j)) {
f[i][j] = f[i - 1][j - 1];
}
//忽略了默认赋值
}
}
}
return f[m][n];
从状态转移方程知道，计算第i行状态只需要第i-1行，所以二维状态dp[i][j]可以压缩成一维dp[j]。下表中标出了计算dp[i][j]所需的元素，更新第dp[i][j]时，dp[j-2]=dp[i][j-2]可以直接替换，而dp[i-1][j-1]已经被覆盖了，需要单独定义pre来保存，同时用cur保存更新前的dp[i-1][j], 更新完后将pre=cur，详见下方代码。
| j-2 | j-1 | j | |
|---|---|---|---|
| i-1 | O | O | |
| i | O | dp[i][j] |
初始化也需要修改，参考下面的dp表格示意图。画出dp表格示意图，有助于理清初始化思路。二维dp[i][j]初始化时，只需要dp[0][0]=true, 其它均为false。压缩为一维dp[j]后，初始化会变复杂。
- 初始化dp[0]。压缩为一维后，每一行都需要初始化。 i=0时，dp[0]=true；而i>0时，dp[0]=false。
- 初始化pre。j是从1开始计算的，所以pre=dp[i-1][0]。 当i=1时，pre=dp[0]=true, 其它情况下pre=false。
- 初始化dp[j>0]。如果二维dp[i][j]更新公式是完美的，那么无需修改。但是在上面的代码中有简化，利用了dp[i][j]默认初始化为false。在改成一维dp[j]时，如果照搬代码，会导致dp[j]继承上一行的结果dp[i-1][j]，而dp[i-1][j]可能是true，从而产生错误。为了防止这个问题，更新dp[j>0]时，可以先将其初始化为false，保证结果正确。
// boolean[][] f = new boolean[m + 1][n + 1];
// f[0][0] = true;
boolean[] f=new boolean[n+1];
for (int i = 0; i <= m; ++i) {
f[0]=(i==0)?true:false;
boolean pre=(i==1)?true:false;
for (int j = 1; j <= n; ++j) {
boolean cur=f[j];
f[j]=false;//防止直接继承f[i-1][j]的结果
if (p.charAt(j - 1) == '*') {
// f[i][j] = f[i][j - 2];
f[j]=f[j-2];
if (matches(s, p, i, j - 1)) {
// f[i][j] = f[i][j] || f[i - 1][j];
f[j]=f[j] || cur;
}
} else {
if (matches(s, p, i, j)) {
// f[i][j] = f[i - 1][j - 1];
f[j]=pre;
}
}
pre=cur;
}
// System.out.println(Arrays.toString(f));
}
// return f[m][n];
return f[n];
188. 买卖股票的最佳时机 IV，3维dp压缩到2维
188. 买卖股票的最佳时机 IV
状态压缩的代码见动态规划+状态压缩。
状态压缩前的代码为：
int[][][] dp=new int[n][2][k1+1];//最多k次交易
//初始化i=0状态
for(int k=0;k<=k1;k++){
dp[0][0][k]=0;//第0天不买，交易次数为0次，利润为0, 所以k>=0均为0。
dp[0][1][k]=(k>=1)?-prices[0]:Integer.MIN_VALUE;//第0天买，交易次数为1，所以需要k>=1，利润为-prices[0]。交易1次，而k=0是非法的，用-inf表示。
}
for(int i=1;i<n;i++){//对应于i=0初始化
for(int k=1;k<=k1;k++){//k=0不用算，就是初始状态
dp[i][0][k]=Math.max(dp[i-1][0][k], dp[i-1][1][k]+prices[i]);//卖出时k不变
dp[i][1][k]=Math.max(dp[i-1][1][k], dp[i-1][0][k-1]-prices[i]);//买入是k加1
}
}
return dp[n-1][0][k1];//最多交易k1次，是0~k1的最大值
从状态转移方程看到，计算第i天结果仅需要第i-1天数据，所以可以将3维dp[i][j][k]压缩为2维dp[j][k]，状态压缩的代码如下。有几点需要说明：
- k的遍历需要倒序。因为dp[i][1][k]依赖于dp[i-1][0][k-1]，需要先更新大的k，才不会影响小的k。
- 需要先更新dp[0][k]，在更新dp[1][k]，这样等式右侧才是i-1的。如果先更新dp[1][k]，就需要临时变量存储更新前的值，便于在dp[0][k]中正确使用。
// int[][][] dp=new int[n][2][k1+1];//最多k次交易
int[][] dp=new int[2][k1+1];//压缩3维为2维
//用i=0初始化
// for(int k=0;k<=k1;k++){
// dp[0][0][k]=0;//第0天不买，交易次数为0次，利润为0, 所以k>=0均为0。
// dp[0][1][k]=(k>=1)?-prices[0]:Integer.MIN_VALUE;//第0天买，交易次数为1，所以需要k>=1，利润为-prices[0]。交易1次，而k=0是非法的，用-inf表示。
// }
//用i=0初始化
for(int k=0;k<=k1;k++){
dp[0][k]=0;//第0天不买，交易次数为0次，利润为0, 所以k>=0均为0。
dp[1][k]=(k>=1)?-prices[0]:Integer.MIN_VALUE;//第0天买，交易次数为1，所以需要k>=1，利润为-prices[0]。交易1次，而k=0是非法的，用-inf表示。
}
// for(int i=1;i<n;i++){//对应于i=0初始化
// for(int k=1;k<=k1;k++){//k=0不用算，就是初始状态
// dp[i][0][k]=Math.max(dp[i-1][0][k], dp[i-1][1][k]+prices[i]);
// dp[i][1][k]=Math.max(dp[i-1][1][k], dp[i-1][0][k-1]-prices[i]);
// }
// }
for(int i=1;i<n;i++){//对应用i=0初始化
for(int k=k1;k>=1;k--){//k逆序，是因为依赖于k-1
dp[0][k]=Math.max(dp[0][k], dp[1][k]+prices[i]);//这两式顺序不能颠倒
dp[1][k]=Math.max(dp[1][k], dp[0][k-1]-prices[i]);//依赖于k-1，所以逆序遍历k
}
}
return dp[0][k1];
扫一扫
757
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
