Leetcode 141环形链表

最新推荐文章于 2025-02-08 18:06:45 发布

wwxy261

最新推荐文章于 2025-02-08 18:06:45 发布

阅读量83

点赞数

CC 4.0 BY-SA版权

分类专栏：算法

本文链接：https://blog.youkuaiyun.com/wwxy1995/article/details/85309618

算法专栏收录该内容

3633 篇文章

订阅专栏

本文介绍了一种使用快慢指针方法判断链表中是否存在环的高效算法。通过实例展示了不同情况下链表环的检测过程，包括链表尾部连接到不同节点的情况。文章深入探讨了如何在O(1)内存限制下解决此问题。

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

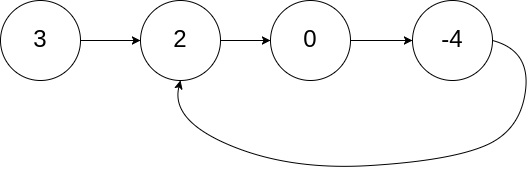
示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

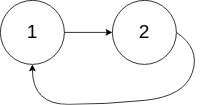
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

同样是快慢指针方法，注意快指针两倍速移动，慢指针一倍速度移动。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) 
    {
        ListNode* currentA;
        ListNode* currentB;
        currentA = head;
        if(!head||!head->next)
            return false;
        currentB = head->next;
        
        while(currentA!=currentB)
        {
            if(!currentB||!(currentB->next))
                return false;
            currentA = currentA->next;
            currentB = currentB->next->next;   // 2倍速度移动
        }
        
        return true;

    }
};