冒泡排序及其优化

最新推荐文章于 2025-07-26 21:13:40 发布

原创最新推荐文章于 2025-07-26 21:13:40 发布 · 122 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #排序算法 #python

冒泡排序

冒泡排序（英语：Bubble Sort）是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序算法的运作如下：

比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数
针对所有的元素重复以上的步骤，除了最后一个
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较

冒泡排序分析

交换过程图示（第一次）：
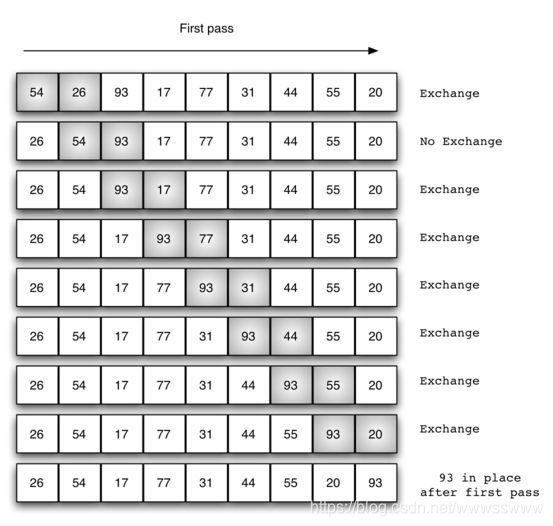
在这里插入图片描述

从上述图示来看交换第一次是第一个元素和后一个元素进行比较如果前者元素大于后者元素则进行交换，这个过程一直到第一次结束，那我们可以写出交换一次的代码：

a=[8,4,5,6,2,3,5,7,1]
n=len(a)
for i in range(0,n-1):
    if a[i]>a[i+1]:
        a[i],a[i+1]=a[i+1],a[i]
print(a)

可以看出列表里面的第一个元素也是列表中最大的元素到了列表的最后一位，说明我们的交换第一次的过程成功了。那接下来我们就要完成所有的交换，我们可以把代码块封装起来：

def mao(alist):
    n=len(alist)
    for j in range(0,n-1):
        for i in range(0,n-1-j):
            if alist[i]>alist[i+1]:
                alist[i],alist[i+1]=alist[i+1],alist[i]
a=[8,4,5,6,2,3,5,7,1]
mao(a)
print(a)

对于我们上面写的代码来看，它的时间复杂度T(n)=O(n*n)=O(n**2),这也是这个程序的最坏时间复杂度，那如果一开始列表的大小顺序都是已经排好的呢，我们就因该考虑最优时间复杂度，则对上面程序进行优化：

def mao(alist):
    n=len(alist)
    for j in range(0,n-1):
        count=0
        for i in range(0,n-1-j):
            if alist[i]>alist[i+1]:
                alist[i],alist[i+1]=alist[i+1],alist[i]
                count+=1
        if count==0:
            return 
a=[8,4,5,6,2,3,5,7,1]
mao(a)
print(a)