数据结构与算法优化实战-优快云博客

本文链接：https://blog.youkuaiyun.com/wwwsswww/article/details/103751240

数据结构算法引入

我们举一个可能不太恰当的例子：
如果将最终写好运行的程序比作战场，我们码农便是指挥作战的将军，而我们所写的代码便是士兵和武器

那么数据结构和算法是什么？

答曰：兵法！我们可以不看兵法在战场上肉搏，如此，可能会胜利，可能会失败。即使胜利，可能也会付出巨大的代价。我们写程序亦然：没有看过数据结构和算法，有时面对问题可能会没有任何思路，不知如何下手去解决；大部分时间可能解决了问题，可是对程序运行的效率和开销没有意识，性能低下；有时会借助别人开发的利器暂时解决了问题，可是遇到性能瓶颈的时候，又不知该如何进行针对性的优化。如果我们常看兵法，便可做到胸有成竹，有时会事半功倍！同样，如果我们常看数据结构与算法，我们写程序时也能游刃有余、明察秋毫，遇到问题时亦能入木三分、迎刃而解。故，数据结构和算法是一名程序开发人员的必备基本功，不是一朝一夕就能练成绝世高手的。冰冻三尺非一日之寒，需要我们平时不断的主动去学习积累。

第一次尝试

下来我们来看看这样一道题：

如果 a+b+c=1000，且 a^2+b2=c^2（a,b,c 为自然数），如何求出所有a、b、c可能的组合

这道题是一个很普通的题，这道题最笨也是最简单的一种做法叫做枚举法，意思就是我门把 a,b,c 每个变量都取1000次使他们的组合去和条件做比较把满足条件的组合打印出来，这就叫枚举法
下来看代码：

import time
start_time=time.time()
for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a**2+b**2==c**2  and a+b+c==1000:
                print("a:{}b:{}c:{}".format(a,b,c))
end_time=time.time()
print("消耗时间:{}".format(end_time-start_time))

运行结果：
在这里插入图片描述

从运行结果看出从程序开始到程序结束花费了200多秒的时间，在计算机计算上慢一秒都是一个很长的时间，为了程序能更快刚好的工作，我对上面程序做了改进：

import time
start_time=time.time()
for a in range(0,1001):
    for b in range(0,1001-a):
        c=1000-a-b
        if a**2+b**2==c**2:
            print("a:{}b:{}c:{}".format(a,b,c))
end_time=time.time()
print("消耗时间:{}".format(end_time-start_time))

运行结果：
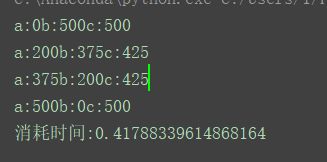
在这里插入图片描述

这是为什么呢！！！ why？？？

对于同一问题，我们给出了两种解决算法，在两种算法的实现中，我们对程序执行的时间进行了测算，发现两段程序执行的时间相差悬殊（214.583347秒相比于0.417秒），由此我们可以得出结论：实现算法程序的执行时间可以反应出算法的效率，即算法的优劣

时间复杂度与"大O记法"

对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。

时间复杂度的几条基本计算规则

1.基本操作，即只有常数项，认为其时间复杂度为O(1）
2.顺序结构，时间复杂度按加法进行计算
3.循环结构，时间复杂度按乘法进行计算
4.分支结构，时间复杂度取最大值
5.判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
6.在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

算法分析

1.枚举法：

import time
start_time=time.time()
for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a**2+b**2==c**2  and a+b+c==1000:
                print("a:{}b:{}c:{}".format(a,b,c))
end_time=time.time()
print("消耗时间:".format(end_time-start_time))

时间复杂度：
T(n)=O(nnn)=O(n**3)

2.算法更新：

import time
start_time=time.time()
for a in range(0,1001):
    for b in range(0,1001-a):
        c=1000-a-b
        if a**2+b**2==c**2:
            print("a:{}b:{}c:{}".format(a,b,c))
end_time=time.time()
print("消耗时间:{}".format(end_time-start_time))