基于干扰的车载自组织网络服务质量与容量分析 用于安全应用
摘要
当前IEEE 802.11p通信系统是否满足安全应用对严格服务质量(QoS)的要求,目前尚不十分明确。在一维(1‐D)高速公路和二维(2‐D)交叉路口道路中,信干噪比(SINR)分布在量化IEEE 802.11p的服务质量及链路容量方面起着关键作用。大多数基于随机几何的解析模型假设采用ALOHA接入来分析SINR分布,而少数研究虽然建立了基于随机几何且考虑CSMA接入的模型,但使用统计估计器推导SINR分布。另一方面,现有的基于干扰的概率解析模型由于在二维(2‐D)场景下数值计算复杂度过高,限制了从一维向二维的扩展。本文提出了一种更通用的解析模型,适用于更一般的非齐次泊松过程(NHPP)节点分布、更一般的包含路径损耗和噪声的衰落信道模型(Nakagami),用于研究在一维高速公路和二维交叉路口道路中基于基本安全消息(BSM)的安全应用车载自组织网络(VANET)的服务质量与容量。该模型通过概率论和顺序统计量评估SINR分布,进而推导VANET BSM广播的服务质量与容量,其计算复杂度远低于无序统计量模型。所提模型通过NS2仿真进行了验证,并进一步扩展用于推导其他服务质量度量指标,如分组接收概率、分组接收率和广播链路容量等。文中实现了对一维与二维场景的性能比较,并讨论了向多交叉口扩展以及增大干扰范围时的服务质量敏感性分析。
索引词
容量,服务质量,安全应用,信干噪比,车载自组织网络。
I. 引言
A. 动机
基于专用短程通信(DSRC)无线电技术在5.9 GHz频段分配的10 MHz信道上进行的车对车(V2V)安全通信,预计可支持低延迟和可靠的无线数据通信,以实现智能交通系统(ITS)中的碰撞预防安全应用。DSRC的主要安全操作是传输两类安全消息:基本安全消息(BSM,也称为信标)和事件驱动安全消息(ESMs)。周期性的BSM传递有关车辆状态的信息(例如位置、速度、方向等)。突发性的事件驱动安全消息(ESMs)则包含有关紧急情况(例如突然急刹车、交叉路口碰撞警告、接近救护车警告等)以及环境危害的信息。基于DSRC系统的车载自组织网络(VANETs)采用单跳或多跳广播方式传播实时交通信息或与安全相关的信息。在已确定的75种与安全相关的应用场景中,典型的一维(1‐D)和二维(2‐D)交叉路口车载网络安全部分的性能分析已被认为是车对车通信中的关键且常见的情况。IEEE 802.11p作为DSRC的物理层(PHY)和媒体访问控制层(MAC layer)标准,已用于支持安全应用的车对车通信。IEEE 802.11p的性能受多种因素影响,如车辆位置、车辆密度、信道状况、网络拓扑结构等。先前的研究表明,在高密度情况下,IEEE 802.11p的性能会下降,并且在典型的一维(1‐D)和二维(2‐D)交叉路口场景中无法保证可靠性指标要求。
信干噪比分布在量化车载自组织网络的服务质量以及链路容量方面起着重要作用。主要的数学工具是随机几何理论和概率建模。大多数基于随机几何和点过程的模型可用于对ALOHA接入进行建模,因为ALOHA具有解析可处理性[12][13][14]。很少有研究使用随机几何来建模基于CSMA的MAC协议。文献[15]中的作者利用ALOHA来近似CSMA MAC协议,以分析密集的车载网络。文献[10]提出的工作则集中于结合排队论和改进的马特恩硬核过程,以刻画CSMA退避过程并捕捉并发传输特性。然而,该模型无法推导出信干噪比分布。
从理论上进行分析,且获取信干噪比的统计值仍然严重依赖通过仿真得到的统计参数值。Ni et al.[16] 和 Ma et al.[17] 假设车辆呈对数正态分布,并通过干扰距离分布以及干扰功率分布获得信干噪比分布。然而,信干噪比分布复杂的数值积分运算使得计算负荷非常高,因此一维建模技术以及车辆对数正态分布假设无法扩展到二维交叉路口以分析信干噪比分布。
我们通过顺序统计量,合理地对干扰距离分布进行了建模,考虑了发射器到干扰源的距离分布以及发射器到接收器的距离,涵盖了一维以及二维交叉路口道路的情况。所提出的模型集中考虑了车辆泊松齐次过程分布、Nakagami衰落信道和噪声影响的合理假设。首先借助顺序统计量推导出干扰距离分布,进而获得接收器处的累积功率分布,从而解析地推导出信干噪比以及链路容量分布。通过结合SUMO(微观交通仿真)移动性模型车辆[18]的NS2仿真,验证了所提出模型的有效性和精度。
B. 相关工作
已提出大量解析模型以及广泛的仿真,用于研究一维高速公路车载自组织网络和二维交叉路口下专用短程通信IEEE 802.11p广播服务的性能与可靠性。仿真模型在测试系统参数组合时耗时较长,而解析模型能够刻画真实的交通状况以降低计算负载,并提供具有洞察力的优化方案来增强专用短程通信的能力。这些模型主要分为两类建模技术:基于确定性通信范围的模型和基于干扰的模型。
大多数基于确定性通信范围的一维解析模型为[19][20][21][22][8],而针对交叉路口二维车载自组织网络的模型为[23][24]。确定性解析模型假设通信范围是确定性的,考虑了隐藏终端、Nakagami衰落模型或Rayleigh衰落信道模型,以及点对点的分组接收概率(PRP)和分组接收率(PRR),这些是用于评估IEEE 802.11p的可靠性指标。然而,确定性通信范围的假设并不切合实际,此外,为了便于解析模型的推导,还引入了许多不切实际的假设,例如车辆分布呈指数分布、具有路径损耗的Rayleigh衰落信道模型等。同时,这类模型也无法量化用于评估链路或整个车载自组织网络实际性能的网络性能指标——链路容量。
基于干扰的模型主要采用随机几何和概率方法来表征IEEE 802.11p的行为,而可靠性评估则依赖于信干噪比分布的数值解。随机几何方法[25]考虑车辆位置、道路几何结构和干扰几何,假设干扰车辆节点遵循泊松点过程(PPP),并利用马特恩核心过程统计地获得信干噪比(SINR)分布。已有若干基于随机几何方法的模型被提出,用于分析一维车载自组织网络[26][10][15][27][28]和交叉路口处二维车载自组织网络中车对车通信在安全应用方面的性能[14][29][12][13][30]。此外,[31][32][33]聚焦于利用复杂的泊松线考克斯过程对蜂窝车联网(C‐V2X)进行建模,以给出相关的服务质量度量,如覆盖概率、速率覆盖,etc。[31]提出了一种新型异构蜂窝网络,包含平面基站和车载基站,用以分析道路上典型用户所感知的覆盖概率。该分析集中在使用帕尔姆概率的网络快照,并假设传输模型中采用Rayleigh衰落信道、基于距离的路径损耗,且噪声功率可忽略不计。[32]分析了考虑空间模型中阴影效应的C‐V2X下行链路基于信干比的覆盖概率和速率覆盖。[33]直接对C‐V2X和基础设施模式下的车对车与蜂窝上行链路频率共享进行了建模,以提高频谱效率。上述工作研究了C‐V2X框架,重点关 注基站、车辆节点以及蜂窝下行链路或上行链路之间的耦合关系,而非针对一维和二维情况下的载波侦听多址接入(CSMA)。因此,这些模型无法直接用于分析车对车通信中CSMA的性能。大多数基于随机几何的模型假设采用ALOHA信道接入、泊松节点分布以及Rayleigh信道衰落模型[12][14][29][27][28][30]。在[12]中,分析了一维和二维交叉路口用户的成功概率。[30]关注视距和非视距场景下车对车通信的可靠性。[14]提出了一个考虑交叉路口车辆聚类效应的空间解析模型,利用发射机概率以及接收器与发射器之间的距离来刻画聚类效应。文献[29]建立了一个适用于事故易发交叉口场景的通用框架,用于分析分组接收概率,并简单考虑了ALOHA情形,获得了数值信干噪比分布。[27][28]专注于研究城市结构如何影响路侧单元(RSU)的布设或交叉路口处的车对车通信,而文献[27]则致力于实现最优传输范围控制,从而获得性能增益。然而,上述所得模型仅适用于ALOHA信道接入和Rayleigh衰落,因其具有可解析处理的优点,尽管适用于不同的一维或二维场景。[15][13]在车载自组织网络高密度条件下使用ALOHA近似CSMA,并在[13]中研究了中断概率的闭式解析表达式。[10]假设采用CSMA信道接入、泊松节点分布和Rayleigh信道衰落模型,并考虑了噪声影响。然而,该研究未获得信干噪比分布的闭式解析表达式,而是通过硬核过程在空间、中等和高密度情况下统计地获取信干噪比分布。Ni et al. 和 Ma et al.[16][17]在提出的一维场景概率模型中未考虑噪声影响,且计算信干噪比分布的计算复杂度过高,难以适用于服务质量与容量的分析。
C. 我们提出的模型与挑战
我们提出了一个解析模型,该模型考虑了 Nakagami 衰落、车辆 NHPP 分布以及噪声影响,适用于一维和二维交叉路口。我们假设车辆节点遵循 NHPP 分布,以刻画真实的交通状况以及交通信号灯的影响[24][34]。在一维和二维情况下,干扰区域的数量以及每个区域内干扰车辆节点是否处于发送状态可能存在多种组合,每种组合的发生概率可根据车辆处于发送状态的概率推导得出,用于解析模型[8]。通过全概率(包含正在发送的干扰节点和噪声影响),可进一步获得干扰距离分布。由此,可解析求解信干噪比分布,进而得到链路容量分布。传输范围、载波侦听范围和干扰范围的参数根据文献[35][16]进行了合理设定。我们提出的模型基于概率建模而非随机几何方法,结合道路几何结构(一维和二维),能够更实际且有效地评估安全应用的服务质量度量及车载自组织网络容量。所提出的解析模型可用于网络设计决策,以及自适应方案对通信网络参数进行调整,以根据可用的链路容量实现最佳服务质量[36][11]。
推导信干噪比的累积分布函数(CDF)主要面临三个挑战。第一个挑战是使信干噪比的解析CDF具有数值解且计算负载较小。然而,仅在对数正态节点分布的一维高速公路场景中,数值积分带来的巨大计算负载限制了该模型在车载自组织网络安全应用设计与规划中的广泛应用[16][17]。我们引入顺序统计量 fDS (发送节点与接收节点之间的距离分布)和 fDi( i= I1, I2, I3, I4,干扰节点与接收节点之间的距离分布),以降低信干噪比分布的计算复杂度。得益于非齐次泊松过程(NHPP)节点分布,公式得到了极大简化。引入顺序统计量后,[16],[17]的计算复杂度可降低 O(n)倍,并变为常数。同理,一维高速公路和二维交叉路口的计算复杂度分别可降低 O(n 2 )倍和O(n 4 )倍。其中,“n”为通信范围内车辆数的上限。
第二个挑战是使用NS2仿真结果对我们提出的模型进行交叉验证。在NS2中,Chen 等[37],[38]为IEEE 802.11协议设计并开发了改进模块,这些模块被研究人员广泛用于车载自组织网络的仿真。该修改版本采用了信干噪比基于该方法来确定是否接收到传入信号。然而,信干噪比门限(SINRTs)是根据调制方式和对应的数据速率设定的固定值。Li 等[38]已指出这种固定的SINRT设置缺乏灵活性,因此我们进一步修改了NS2源代码并进行编译,使其能够在仿真中根据用户需求自适应地调整SINRT设置。
第三个挑战是给出基于顺序统计量和无序统计量的信干噪比累积分布函数比较的计算复杂度,从而验证我们所提出模型的有效性。由于车载自组织网络服务质量的数值解需要大量计算时间,因此采用蒙特卡洛以及消息传递接口(MPI)方法[39]来计算基于无序统计模型的信干噪比分布。
D. 贡献
本文的主要贡献总结如下:
- 在考虑CSMA接入、Nakagami信道衰落与路径损耗、噪声影响以及隐藏终端和并发传输影响的情况下,基于信干噪比(SINR)的解析模型在具有非齐次泊松过程(NHPP)节点分布的一维高速公路和二维交叉路口场景中建立;
- 所提出的模型通过一种新的NHPP顺序统计量方法推导出信干噪比分布的闭式解析表达式,显著降低了推导过程的计算复杂度;
- 采用蒙特卡洛方法以及MPI方法对无序统计模型进行计算,实验结果给出了基于顺序统计量模型与无序统计量模型之间的计算复杂度比较;
- 定义并评估了服务质量度量(QoS Metrics)和容量指标(Capacity Metrics),如链路容量;
- 我们设计了新的 WirelessPhy类,使NS2仿真能够适应灵活的SINRT设置。
组织结构
本文的其余部分组织如下:第二节介绍了针对一维车载自组织网络的解析模型,以及关于非齐次泊松过程节点分布、噪声影响和带有路径损耗的中村信道衰落的假设,并在此基础上构建了解析模型,获得了一维情况下的服务质量可靠性及容量指标。第三节提出了针对二维车载自组织网络的解析模型,假设干扰来自X轴左右方向以及Y轴上下方向,并提出了一种基于非齐次泊松过程有序统计量的方法,以降低信干噪比累积分布函数的计算复杂性,从而得到二维情况下的服务质量与容量指标。第四节修改了NS2中无线模块的源代码,以实现SINRT的灵活设置,给出了车辆位置服从非齐次泊松过程的一维和二维场景的参数设置,并基于SUMO和NS2内置移动模型生成的交通流,比较了静态场景仿真与移动性场景仿真的性能。第五节给出了顺序统计量之间的计算效率比较模型和无序情况,展示了数值与仿真结果的对比,分析了一维和二维场景之间的性能差异,并给出了不同车载自组织网络场景下链路容量的概率密度函数(PDF)。第六节进一步获得了考虑载波侦听范围之外多个交叉路口的 PRR。本文在第七节进行了总结。
II. 一维车载自组织网络中信标消息广播的服务质量与容量
A. 假设和信道模型
我们假设IEEE 802.11p信标消息广播在以下场景下工作。
1. 二维条带状网络区域可近似为一维单车道。
2. 所有车辆均配备专用短程通信功能。
3. 所有节点被视为具有相同车辆长度 LV和传输功率 Pt的同质节点。
4. 移动节点根据非齐次泊松过程(NHPP)沿线路分布,距离标记节点 x处的车辆密度为 β(x)(单位:每米节点数)。则在空间区间(x, x+ l)内发现 i个车辆的概率由以下公式给出
$$
P[i,(x, x+ l)]=\frac{(\int_{x}^{x+l} \beta(z)dz)^i \exp(-\int_{x}^{x+l} \beta(z)dz)}{i!}.
$$
5. 信道衰落效应:中村衰落模型。
6. 根据[35]和[16], 干扰源与标记发射机之间的距离不应超过2rE,该结论已被证实非常准确。 rE是平均感知范围rE= d0 α√Ptη/Pth,而 Pth是空闲信道评估(CCA)灵敏度。
源节点距离 d 处接收到的功率 Pr 的概率密度函数由以下公式给出
$$
f_{Pr |d}(x)= \frac{1}{\Gamma(m)}\left( \frac{m}{\bar{P}_r(d)} \right)^m x^{m-1} \exp\left(- \frac{mx}{\bar{P}_r(d)} \right) ,
$$
其中 Γ(·)是伽马函数, m是衰落参数。 $\bar{P}_r(d)= P_t\eta( \frac{d_0}{d})^\alpha$ (η是由收发器确定的常数,d0是远场区的参考距离, α是路径损耗指数)是由路径损耗决定的均值。
B. SINR的CDF
许多研究将 $P(\text{信干噪比} > \theta) = 1 - P(\text{信干噪比} \leq \theta)$ 视为评估车载自组织网络性能的重要标准,我们的研究也分析了信干噪比累积分布函数的推导。$\text{信干噪比}= P_r /(P_I + P_n)$,其中 $P_r$ 是接收到的信号功率, $P_I$ 是接收器处的干扰功率,$P_n$ 是噪声功率。当存在正在发送的干扰节点,而 $P_I$ 远大于$P_n$ 时,则信干噪比可近似表示为$\text{SINR}_I = P_r /P_I$。否则,信干噪比可以表示为$\text{SINR}_n= P_r/P_n$,记作无干扰源时的信干噪比。因此,信干噪比的概率密度函数和累积分布函数可分别基于$\text{SINR}_I$和 $\text{SINR}_n$出现的概率推导得出。
信干噪比I的概率密度函数可通过 Pr和 PI的卷积商公式求得,其中(1)给出了 Pr的概率密度函数,而假设 Pn为常数时,信干噪比n的概率密度函数可由 Pr的概率密度函数得到。从上述分析可知,主要问题在于推导 $P_I$ 的概率密度函数,其中应首先建立干扰距离分布的公式,然后表示如下。
C. 干扰距离分布
如图1所示,在[16]中, rE和 rT分别表示信道感知范围和传输范围,其中$r_T \leq r_E$[16]。 DS表示源节点T与目标节点 R之间的距离。 I1(I2)是右侧(左侧)阴影区域内的干扰节点,其到 T的距离为[rE, 2rE]。假设右侧(左侧)阴影区域内有 l(l′)个节点, di 1( i1= 1,…, l)(di 2( i2= 1,…, l′))表示标记节点 T与右侧(左侧)阴影区域内的第 i1(i2)个节点之间的距离。 DI 1( DI 2) 表示干扰节点 I1( I2)到 R, DI 1 + DS= di 1( DI 2 =DS+ di 2) 的距离。

给定节点间距离的泊松过程分布,以及表示右侧阴影区域内车辆与节点之间无序距离的独立随机变量 $r_E \leq S_{i1} \leq 2r_E$。设区间[rE, r]、[rE, 2rE]内的车辆数分别记为 N(r)、 N(s)。$S_{i1}$ 的累积分布函数由[40]中的定理 6.2给出。
$$
F_{S_{i1}} (r)= P(S_{i1} \leq r|N(r_E)= 1)
=
\frac{P[N(r)= 1, N(s)- N(r)= 0]}{P[N(s)= 1]}
=
\frac{\int_{r}^{r_E} \beta(z)dz}{\int_{2r_E}^{r_E} \beta(z)dz} , r_E \leq r \leq 2r_E , i1= 1,…, l.
$$
然后$S_{i1}$ 的概率密度函数为:
$$
f_{S_{i1}} (r)=
\frac{\beta(r)}{\int_{2r_E}^{r_E} \beta(z)dz} .
$$
然后根据[40]中的定理6.2, $d_{i1} (i1 = 1,…, l)$是随机变量 $S_{i1} (i1 = 1,…, l)$的顺序统计量。因此,距离 $d_{i1} (r_E \leq d_{i1} \leq 2r_E)$的累积分布函数和概率密度函数可以计算为
$$
F_{d_{i1}}(\tau)= P(d_{i1} \leq \tau)=
\sum_{j=i1}^{l}\binom{l}{j} F_{S_{i1}}^j(\tau)[1 - F_{S_{i1}}(\tau)]^{l-j},
$$
$$
f_{d_{i1}}(\tau)= \frac{dF_{d_{i1}}(\tau)}{d\tau} , r_E \leq \tau \leq 2r_E.
$$
设$D_S= d_s$,假设 I1是右侧阴影区域中的第 i1个节点。$D_{I1}$ ($r_E - D_s \leq D_{I1} \leq 2r_E - D_s$)的条件累积分布函数可定义为
$$
F_{D_{I1} |(d_s,i1)}(x)= P(D_{I1} \leq x|d_s) = P(d_{i1} - d_s \leq x|d_s) = P(d_{i1} \leq x+ d_s|d_s)
= F_{d_{i1}}(x+ d_s), i1= 1,…, l.
$$
单个干扰节点到接收器的距离的PDFs R 可表示为
$$
f_{D_{I1} |(d_s,i1)}( x)=
\frac{dF_{D_{I1} |(d_s,i1)}( x)}{dx}
= f_{d_{i1}}(x+ d_s).
$$
阴影区域中有 l 个节点的概率是
$$
P[l,(r_E, 2r_E)]=\frac{(\int_{r_E}^{2r_E} \beta(x)dx)^l \exp(-\int_{r_E}^{2r_E} \beta(x)dx)}{l!}.
$$
然后,$D_{I1}$ 的条件概率密度函数可以表示为
$$
f_{D_{I1} |d_s}( x)=
\sum_{l=1}^{\infty}
P[l,(r_E, 2r_E)]
\sum_{i1=1}^{l}
f_{D_{I1} |(d_s,i1)}( x)p_{i1}
,
$$
其中$p_{i1}$ 是干扰源 I1 位于右侧阴影区域内的第 i1个节点的概率,该概率被评估为 $p_{i1} =1/l(i1= 1,…, l)$。因此,(7) 可表示为
$$
f_{D_{I1} |d_s}( x)=
\sum_{l=1}^{\infty}
P[l,(r_E, 2r_E)]
\sum_{i1=1}^{l}
f_{d_{i1}} (x+ d_s)
\frac{1}{l}
= f_{S_{i1}} (x+ d_s)
=
\frac{\beta(x+ d_s)}{\int_{2r_E}^{r_E} \beta(z)dz} .
$$
类似地,也可以推导出 I 2在 R处的干扰功率的累积分布函数和概率密度函数。表示 T与左侧阴影区域中节点之间无序距离的独立随机变量 $S_{i2} (r_E \leq S_{i2} \leq 2r_E)$,其 $S_{i2}$ 的累积分布函数和概率密度函数分别为
$$
F_{S_{i2}} (r)=
\frac{\int_{-r}^{-r_E} \beta(z)dz}{\int_{-2r_E}^{-r_E} \beta(z)dz}
, f_{S_{i2}} (r)=
\frac{\beta(-r)}{\int_{-2r_E}^{-r_E} \beta(z)dz} ,
r_E \leq r \leq 2r_E , i2 = 1, 2,…, l’.
$$
$D_{I2}$ 的概率密度函数可以根据从(4)到(8)的推导过程获得:
$$
f_{D_{I2} |d_s} (x)=
\frac{\beta(d_s - x)}{\int_{-2r_E}^{-r_E} \beta(z)dz} .
$$
(8)、(9) 是干扰节点的距离分布,通过引入顺序统计量进行了简要表述。这样,计算复杂度变为常数。否则,一维情况下式(13)和二维交叉路口情况下式(29)的复杂性分别为 O(n2) 和 O(n4)。后续实验将展示有序与无序情况下的运行时间比较。
D. 含干扰的SINR概率密度函数
根据(1)和(8),R处接收到的I1的干扰功率 PI1的累积分布函数和概率密度函数可以表示为
$$
F_{P_{I1} |d_s}(x)= P(P_{I1} \leq x|D_S= d_s)
= \int_{t’=0}^{x}\int_{t=r_E-d_s}^{2r_E-d_s} f_{P_r|D_{I1}}(t’)f_{D_{I1} |d_s}(t)dtdt’,
$$
$$
f_{P_{I1} |d_s}(x)=
\frac{dF_{P_{I1} |d_s}(x)}{dx} .
$$
I2的干扰功率 PI2在 R处接收到的累积分布函数和概率密度函数可通过(1)和(9)得到:
$$
F_{P_{I2} |d_s}( x)= P(P_{I2} \leq x|D_S= d_s)
= \int_{t’=0}^{x}\int_{t=r_E+d_s}^{2r_E+d_s} f_{P_r|D_{I2}} (t’)f_{D_{I2} |d_s}( t)dtdt’,
$$
$$
f_{P_{I2} |d_s}( x)=
\frac{dF_{P_{I2} |d_s}( x)}{dx} .
$$
[8]构建了一个基于半马尔可夫的排队模型来表征载波侦听多路访问/冲突避免的退避机制,并获得了πXMT,即车辆处于传输状态的稳态概率。根据 πXMT,可评估在标记节点传输的易受攻击期内,阴影区域中的节点进行传输的概率为
$$
p_t= \pi_{XMT} \frac{2(T_p - DIFS)}{T_p},
$$
其中 $T_p$是 XMT状态的平均停留时间,DIFS为分布式帧间间隔。那么,在右侧阴影区域存在干扰的概率为
$$
p_1=1 -
\sum_{i=0}^{\infty}
(1 -p_t)^i\frac{(\int_{r_E}^{2r_E} \beta(x)dx)^i}{i!} \exp(-\int_{r_E}^{2r_E} \beta(x)dx)
= 1 - \exp(-p_t\int_{r_E}^{2r_E} \beta(x)dx),
$$
以及左侧阴影区域存在干扰的概率为
$$
p_2= 1 -
\sum_{i=0}^{\infty}
(1 -p_t)^i \frac{(\int_{-2r_E}^{-r_E} \beta(x)dx)^i}{i!} \exp(-\int_{-2r_E}^{-r_E} \beta(x)dx)
= 1 - \exp(-p_t\int_{-2r_E}^{-r_E} \beta(x)dx).
$$
需要考虑三种情况以获得存在干扰时的信干噪比概率密度函数:
1. 右侧阴影区域存在干扰源,而左侧阴影区域不存在干扰源:概率为 $p_1(1 -p_2)$,干扰功率的概率密度函数为$f_{P_{I1} |d_s}(x)$。
2. 左侧阴影区域存在干扰源,而右侧阴影区域不存在干扰源:概率为 $p_2(1 -p_1)$,干扰功率的概率密度函数为 $f_{P_{I2} |d_s}(x)$。
3. 左侧和右侧阴影区域均存在干扰源:概率为$p_1 \cdot p_2$,干扰功率的概率密度函数为
$$
f_{P_{I1+I2} |d_s}(x)= \int_{0}^{\infty}
f_{P_{I1} |d_s}(x - t)f_{P_{I2} |d_s}(t)dt.
$$
根据全概率公式,接收器 R 处累积的总干扰功率$P_I$的概率密度函数表示为
$$
f_{P_I|d_s}(x)= p_1(1 -p_2)f_{P_{I1} |d_s}(x)
+ p_2(1 -p_1)f_{P_{I2} |d_s}(x)
+ p_1p_2f_{P_{I1+I2} |d_s( x)},
$$
$$
f_{\text{SINR}
I|(d_s,P_r>P
{th})}(x)
= \int_{t=\max{P_{th}/x, P_{th}}}^{\infty}
t \cdot f_{P_r|d_s}( t \cdot x)f_{P_I|d_s}( t)dt.
$$
E. 无干扰情况下的信干噪比概率密度函数
左侧和右侧阴影区域均无干扰源的概率为$(1 -p_1) \cdot(1 -p_2)$,噪声功率被假定为常数,其值为 $P_n$,信干噪比$n= P_r/P_n$。
$$
F_{\text{SINR}
n|(d_s ,P_r >P
{th})}(x) =(1 -p_1)(1 -p_2)P(\text{SINR}
n \leq x|P_r> P
{th})
=(1 -p_1)(1 -p_2)P\left(\frac{P_r}{P_n} \leq x|P_r> P_{th}\right)
=(1 -p_1)(1 -p_2) \frac{P(P_{th}< P_r \leq P_nx)}{1 - P(P_r \leq P_{th})} =(1 -p_1)(1 -p_2)
\frac{F_{P_r |d_s}( P_nx)- F_{P_r |d_s}( P_{th})}{1 - F_{P_r |d_s}( P_{th})}
,
$$
$$
f_{\text{SINR}
n |(d_s ,P_r >P
{th})}( x)
= \frac{dF_{\text{SINR}
n |(d_s ,P_r >P
{th})}( x)}{dx}
=(1 -p_1)(1 -p_2)
\frac{P_nf_{P_r |d_s} (P_nx)}{1 - \int_{0}^{P_{th}} f_{P_r |d_s} (y)dy} .
$$
F. 服务质量度量和链路容量的推导
本小节给出了PRP、PRR和链路容量的定义。
1) Prp
当 $D_S = d_s$ 时,信干噪比的分布可通过(14)和 (16)获得:
$$
f_{\text{SINR}|( d_s ,P_r >P_{th} )}( x)= f_{\text{SINR}
I |( d_s ,P_r >P
{th} )}( x)
+ f_{\text{SINR}
n |( d_s ,P_r >P
{th} )}( x).
$$
由(17)可得信干噪比的条件累积分布函数为
$$
F_{\text{SINR}|(d_s,P_r>P_{th})}(x)= \int_{0}^{x} f_{\text{SINR}|(d_s,P_r>P_{th})}(t)dt.
$$
在标记车辆的干扰范围内,处于同一时隙内且无法被 CSMA协议检测到的车辆传输也可能导致数据包(消息)碰撞,这种情况称为并发碰撞。从 R的传输不发生并发碰撞的概率推导为[22]
$$
P_{\text{con}|d_s}= \exp(-n_\Sigma),
$$
其中$n_\Sigma$是接收节点感知范围内在并发时隙中平均发送的节点数。
接收器与标记节点的距离为 $d_s$时成功接收消息的概率,取决于测得的信干噪比大于给定阈值,并且接收到的信号强度应强于接收阈值 $P_{th}$,其表达式为
$$
\text{PRP}(d_s, \theta)
= P(\text{SINR} \geq \theta|d_s, P_r> P_{th})P_{\text{con}|d_s} = P(\text{SINR} \geq \theta|(d_s, P_r> P_{th})P(P_r> P_{th})P_{\text{con}|d_s}
=(1 - F_{\text{SINR}|(d_s,P_r>P_{th})}(\theta))
(1 -\int_{0}^{P_{th}}
f_{P_r|d_s}( x)dx) P_{\text{con}|d_s} .
$$
2) PRR
将安全应用的感兴趣区域(ROI)定义为参与该应用的实体所覆盖的地理区域的大小,表示为$d_{\text{ROI}}$。不同类型的安全应用具有不同的感兴趣区域(ROI)大小 [41]。
感兴趣区域(ROI)内的分组接收率(PRR)(无传输错误的接收器所占的百分比)可以被评估为
$$
\text{PRR}(d, \theta)= \frac{\int_{0}^{d} \beta(x)\text{PRP}(x, \theta)dx}{\int_{0}^{d} \beta(x)dx} , d \leq d_{\text{ROI}}.
$$
3) 链路容量
利用不含 DS的信干噪比分布来获取链路容量分布, DS的概率密度函数的推导过程与(2)–(8)类似,总的 DS的概率密度函数可表示为
$$
f_{D_S} (x)=
\frac{\beta(x)}{\int_{0}^{r_E} \beta(z)dz} .
$$
信干噪比的PDF和累积分布函数可以推导为
$$
f_{\text{SINR}|( P_r >P_{th} )}( x)= \int_{0}^{r_E}
f_{\text{SINR}|( d_s ,P_r >P_{th} )}( x)f_{D_S} (t)dt,
$$
$$
F_{\text{SINR}|( P_r >P_{th} )}( x)= \int_{0}^{x}
f_{\text{SINR}|( P_r >P_{th} )}( t)dt.
$$
信道的链路容量表示信道传输速率(比特每秒)的上限,该值由根据香农公式:
$$
C= W \log_2(1+ \text{SINR}), \quad C: \text{link capacity}, \quad W: \text{network bandwidth}.
$$
链路容量的累积分布函数可以通过信干噪比的累积分布函数和香农公式获得:
$$
F_C(x)= P(W \log_2(1+ \text{SINR})< x)
= F_{\text{SINR}|(P_r>P_{th})}(2^{x/W} -1).
$$
此外,我们可以得到链路容量的概率密度函数和期望如下:
$$
f_C(x)= \frac{\ln 2}{W} \cdot 2^{x/W} f_{\text{SINR}|(P_r>P_{th})}(2^{x/W} -1),
$$
$$
E(C)= \int_{0}^{\infty}
x f_C(x)dx.
$$
III. 二维车载自组织网络中信标消息广播的服务质量与容量
本节提出了二维交叉路口的解析模型,信干噪比累积分布函数的推导方法与II‐B类似。为不失一般性,采用两种考虑标记发射机与接收器之间位置几何关系的情况,以展示如何对PRP、PRR和容量进行解析推导。在每种情况下,干扰区域数量与是否存在正在发送的干扰节点的组合被汇总于$2^4= 16$,其中干扰区域数量等于4。由于需要追踪多种组合,二维情况的分析相比一维更为复杂。
A. 假设
除了与一维情况相同的假设外,以下假设适用于二维交叉路口场景:
1. 每条交叉道路每个方向有一条车道,因此每个交叉路口可近似为交叉直线。交叉路口与其他交叉路口相距较远,因此通信范围没有重叠。
2. 交叉路口之间的距离远超节点的传输范围。
3. 对标记接收器节点 R的干扰影响可由图2或图3中所示的四边阴影区域近似表示。
假设交叉路口的坐标为(0,0)。给定一个位于$(x_0,0)$的发送节点 T(见图2), R是安全应用中节点 T的感兴趣区域内的接收器之一。 R的位置为$(x_r , 0)$或$(0, y_r)$ $(| x_r - x_0| \leq d_{\text{ROI}} , y_r^2 + x_0^2 \leq d_{\text{ROI}}^2)$ ,我们需要研究每种情况下信干噪比的累积分布函数。SINR的含义、SINR I 和SINRn与一维情况相同。
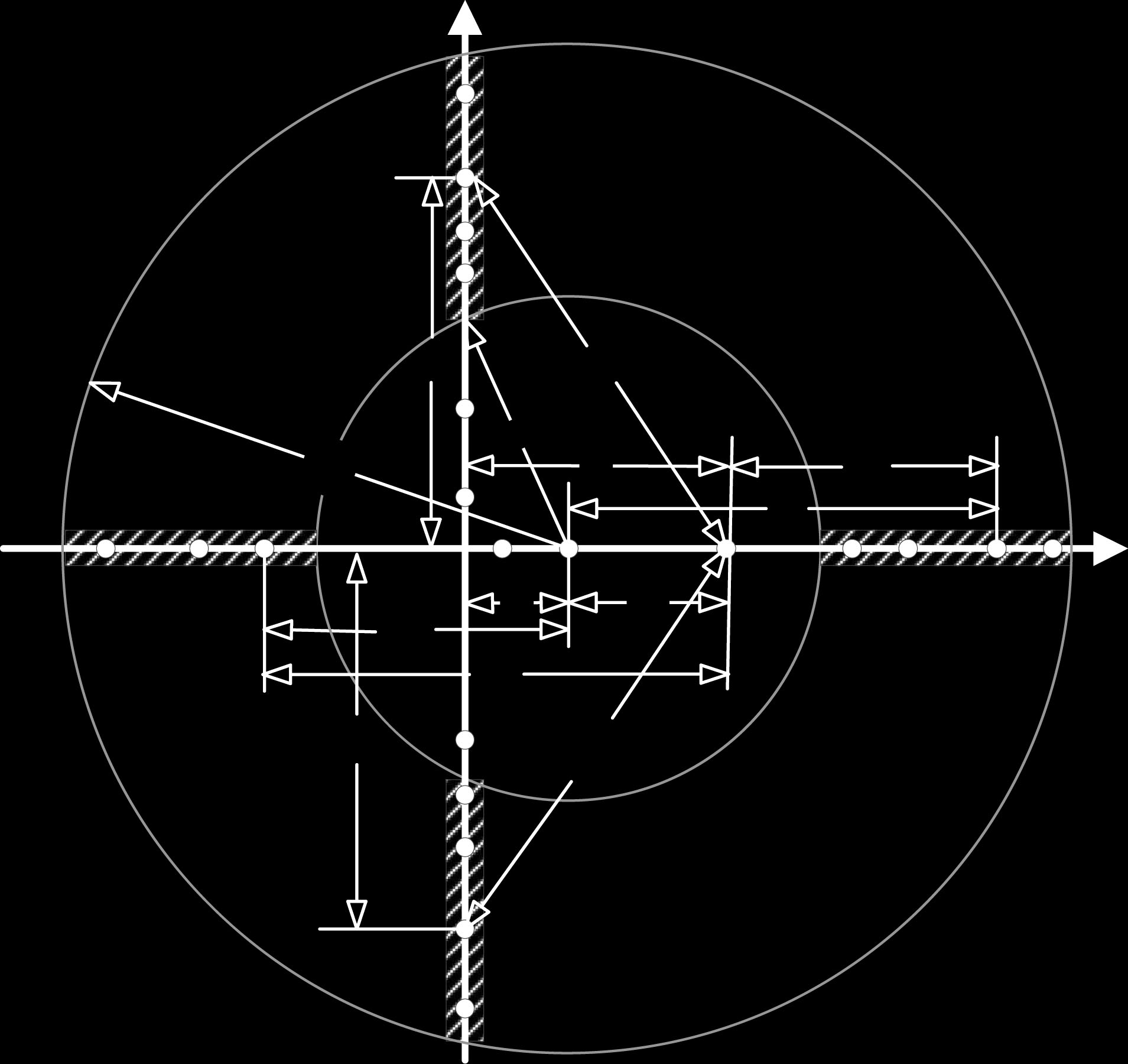
B. 情况 1 R 在$(x_R ,0)$
如图2所示,假设干扰 I 1( I 2)位于X轴上右侧(左侧)阴影区域内,距 T的距离为$[r_E , 2r_E]$,该区域内有 $l(l’)$个节点;干扰 I 3( I 4)位于Y轴上方(下方)阴影区域内,距 T的距离为$[r_E , 2r_E]$,该区域内有 $l’‘(l’‘’)$个节点在此区域内。 $D_{I_k} (k= 1, 2, 3, 4)$ 表示节点 $I_k$ 与 R之间的距离, $D_S$ 表示T 与 R之间的距离。
1) 干扰距离分布
I1和 I2的分布与一维情况相同,但原点坐标从 T变为 O,且 $X_0= x_0(x_0+ d_s = x_r)$。对 (8)和(9)中的坐标变换 $x_0$,得到I1和 I2的概率密度函数:
$$
f_{D_{I1} |( x_0 ,x_r )}( x)= \frac{\beta(x+ x_r)}{\int_{x_0+r_E}^{x_0+2r_E} \beta(z)dz} .
$$
$$
f_{D_{I2} |( x_0 ,x_r )}( x)=
\frac{\beta(x_r - x)}{\int_{x_0-2r_E}^{x_0-r_E} \beta(z)dz} .
$$
I3和 $f_{D_{I3} |}$的$(x_0,x_r)(y)$的概率密度函数按公式(28)给出,具体推导见附录A。
$$
f_{D_{I3} |(x_0,x_r)}(y)=
\frac{\beta(\sqrt{y^2 - x_r^2})}{\int_{\sqrt{r_E^2-x_0^2}}^{\sqrt{4r_E^2-x_0^2}} \beta(z)dz} .
$$
考虑到纵轴上下方相互对称, $D_{I4}$的概率密度函数等于 $D_{I3}$的概率密度函数。
2) 含干扰的信干噪比的PDF
在 R处接收到的干扰功率 $P_{I1}$、 $P_{I2}$和 $P_{I3}$的累积分布函数可以表示为
$$
F_{P_{I1} |(x_0,x_r)}(x)= P(P_{I1} \leq x|(x_0, x_r))
= \int_{t’=0}^{x}\int_{t=r_E-d_s}^{2r_E-d_s} f_{P_r|D_{I1}}(t’)f_{D_{I1} |(x_0,x_r)}(t)dtdt’,
$$
$$
F_{P_{I2} |(x_0,x_r)}(x)= P(P_{I2} \leq x|(x_0, x_r))
= \int_{t’=0}^{x}\int_{t=r_E+d_s}^{2r_E+d_s} f_{P_r|D_{I2}}(t’)f_{D_{I2} |(x_0,x_r)}(t)dtdt’,
$$
$$
F_{P_{I3} |(x_0,x_r)}(y)= P(P_{I3} \leq y|(x_0, x_r))
= \int_{t’=0}^{y}\int_{t=\sqrt{r_E^2-x_0^2}+x_r^2}^{\sqrt{4r_E^2-x_0^2}+x_r^2} f_{P_r|D_{I3}}(t’)f_{D_{I3} |(x_0 ,x_r)}( t)dtdt’.
$$
然后可以推导出$P_{I1} \sim P_{I4}$ 的概率密度函数
$$
f_{P_{I1} |(x_0 ,x_r)}( x)=
\frac{dF_{P_{I1} |(x_0 ,x_r)}( x)}{dx} ,
$$
$$
f_{P_{I2} |(x_0 ,x_r)}( x)=
\frac{dF_{P_{I2} |(x_0 ,x_r)}( x)}{dx} ,
$$
$$
f_{P_{I3} |(x_0 ,x_r)}(y)=
\frac{dF_{P_{I3} |(x_0 ,x_r)}(y)}{dy} .
$$
根据对称性,我们得到以下结果:
$$
f_{P_{I4} |(x_0 ,x_r)}(y)= f_{P_{I3} |(x_0 ,x_r)}(y).
$$
干扰源区域数量与每个区域内是否存在干扰源的组合总数为$2^4= 16$,在总共16种组合中可推导出15种存在干扰的组合类型。当存在多个干扰时,接收节点处干扰功率的 PDF R是其他干扰功率PDFs的卷积和。以下是某些情况下卷积和表达式的一个示例,其他情况类似,此处省略。
$$
f_{P_{I1 I3} |(x_0 ,x_r )}( x)= \int_{0}^{\infty}
f_{P_{I1} |(x_0 ,x_r )}( x - t)f_{P_{I3} |(x_0 ,x_r )}( t)dt,
$$
$$
f_{P_{I2 I4} |( x_0 ,x_r )}( x)= \int_{0}^{\infty}
f_{P_{I2} |( x_0 ,x_r )}( x - t)f_{P_{I4} |( x_0 ,x_r )}( t)dt,
$$
$$
f_{P_{I1-4} |( x_0 ,x_r )}( x)= \int_{0}^{\infty}
f_{P_{I1 I3} |( x_0 ,x_r )}( x - t)f_{P_{I2 I4} |( x_0 ,x_r )}( t)dt,
$$
$$
f_{P_{I1 I2 I4} |( x_0 ,x_r )}( x)= \int_{0}^{\infty}
f_{P_{I1} |( x_0 ,x_r )}( x - t)f_{P_{I2 I4} |( x_0 ,x_r )}( t)dt.
$$
设 $p_1,p_2,p_3$和 $p_4$分别表示右侧、上方、左侧和下方阴影区域中干扰的概率。采用与(11)、(12)相同的方法,可得到以下公式:
$$
p_1= 1 - \exp(-p_t\int_{x_0+r_E}^{x_0+2r_E} \beta(x)dx),
$$
$$
p_3= 1 - \exp(-p_t\int_{x_0-2r_E}^{x_0-r_E} \beta(x)dx),
$$
$$
p_2= p_4= 1 - \exp(-p_t\int_{\sqrt{r_E^2-x_0^2}}^{\sqrt{4r_E^2-x_0^2}} \beta(y)dy).
$$
$ p_t $由公式(10)给出。根据15种存在干扰情况下的干扰功率概率密度函数及每种情况的概率,利用全概率公式得到存在干扰时干扰功率的平均概率密度函数。
$$
f_{P_I|(x_0,x_r)}(x)=
\prod_{i=1}^{4} p_i f_{P_{I1-4} |(x_0,x_r)}(x)
+
\sum_{i=1}^{4}
\left[(1 -p_i)\cdot \prod_{\substack{j=1\j\neq i}}^{4} p_j \cdot f_{P_{\prod_{\substack{j=1\j\neq i}}^{4} I_j} |(x_0,x_r)}( x) \right]
+
\sum_{i=1}^{4}
\left[p_i \prod_{\substack{j=1\j\neq i}}^{4} (1 -p_j)\cdot f_{P_{I_i} |(x_0 ,x_r)}( x) \right]
+
\sum_{i=1}^{3} \left[ \sum_{j=i+1}^{4} p_i p_j \prod_{\substack{k=1\k\neq i,j}}^{4} (1 -p_k)f_{P_{I_i I_j} |(x_0 ,x_r)}( x) \right].
$$
存在干扰时信干噪比的条件概率密度函数
$$
f_{\text{SINR}
I|( x_0 ,x_r ,P_r >P
{th})}(x)
= \int_{t=\max{P_{th}/x, P_{th}}}^{\infty}
t \cdot f_{P_r |(x_0 ,x_r)}( t \cdot x)f_{P_I |(x_0 ,x_r)}( t)dt,
$$
3) 无干扰情况下的信干噪比概率密度函数
类似于(15)、(16),可得无干扰情况下信干噪比的PDF为
$$
f_{\text{SINR}
n |(x_0 ,x_r ,P_r >P
{th})}( x)
=
\prod_{i=1}^{4} (1 -p_i)
\frac{P_n f_{P_r |(x_0 ,x_r)} (P_n x)}{1 - \int_{0}^{P_{th}} f_{P_r |(x_0 ,x_r)} (y)dy} .
$$
4) 服务质量度量
信干噪比的条件概率密度函数可以表示为
$$
f_{\text{SINR}|( x_0 ,x_r ,P_r >P_{th} )}( x)= f_{\text{SINR}
I |( x_0 ,x_r ,P_r >P
{th} )}( x)
+ f_{\text{SINR}
n |( x_0 ,x_r ,P_r >P
{th} )}( x).
$$
信干噪比的条件累积分布函数可以表示为
$$
F_{\text{SINR}|( x_0 ,x_r ,P_r >P_{th} )}( x)= \int_{0}^{x}
f_{\text{SINR}|( x_0 ,x_r ,P_r >P_{th} )}( t)dt.
$$
使用与(21)相同的方法,可以得到 DS的概率密度函数
$$
f_{D_S}(x)=
\frac{\beta(x)}{\int_{x_0}^{x_0+r_E} \beta(z)dz} .
$$
信干噪比的PDF和累积分布函数可以推导为
$$
f_{\text{SINR}|(P_r>P_{th})}(x)= \int_{0}^{r_E} f_{\text{SINR}|(x_0,x_r,P_r>P_{th})}(x)f_{D_S}(t)dt,
$$
$$
F_{\text{SINR}|(P_r>P_{th})}(x)= \int_{0}^{x} f_{\text{SINR}|(P_r>P_{th})}(t)dt.
$$
然后可以评估与标记节点距离为 $d_s$的PRP以及ROI内的PRR
$$
\text{PRP}(d_s, \theta)=(1 - F_{\text{SINR}|{x_0,x_r,P_r>P_{th}}}(\theta))
\times(1 -\int_{0}^{P_{th}} f_{P_r|d_s}(x)dx)\times P_{\text{con}|(x_0,x_r)},
$$
$$
P_{\text{con}|d_s} = \exp(-n_\Sigma(x_0 ,x_r)) ,
$$
$$
\text{PRR}(d, \theta)= \frac{\int_{-d}^{x_0+d} \beta(x)\text{PRP}(x, \theta)dx}{\int_{-d}^{x_0+d} \beta(x)dx} , d \leq d_{\text{ROI}}.
$$
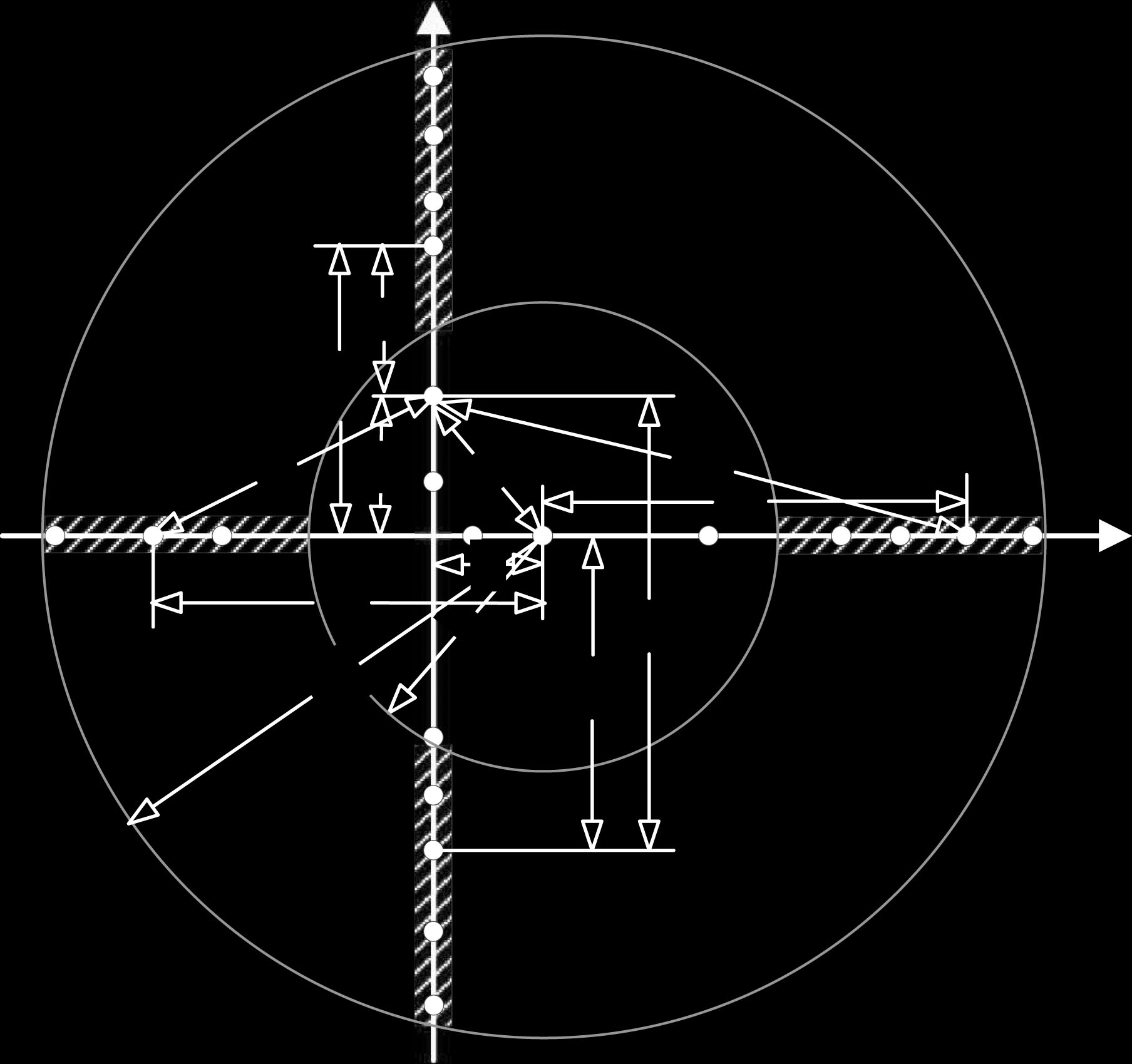
C. 情况 2 R 在$(0,y_r)$ 内
如图3所示,假设干扰 I1(I2)位于X轴上的右侧(左侧)阴影区域内,到 T的距离为$[r_E, 2r_E]$,该区域内有 $l(l’)$个节点;干扰 I3(I4)位于Y轴上的上方(下方)阴影区域内,到 T的距离为$[r_E, 2r_E]$,该区域内有 $l’‘(l’‘’)$个节点。 $D_{I_k}(k= 1, 2, 3, 4)$表示 $I_k$节点到 R的距离, $D_S$表示T与 R之间的距离。
1) 干扰距离分布
$f_{D_{I1} |(x_0 , y_r)}( x)$ 和 $f_{D_{I3} |(x_0 , y_r)}(y)$ 分别表示 $D_{I1}$ 和 $D_{I3}$ 的概率密度函数,其表达式如公式 (38) 所示。公式 (38) 的推导过程见附录B。
$$
f_{D_{I1} |(x_0 , y_r)}( x)= \frac{\beta(\sqrt{x^2 - y_r^2})}{\int_{x_0+r_E}^{x_0+2r_E} \beta(z)dz} ,
$$
$$
f_{D_{I3} |(x_0 , y_r)}(y)=
\frac{\beta(y+ y_r)}{\int_{\sqrt{r_E^2-x_0^2}}^{\sqrt{4r_E^2-x_0^2}} \beta(z)dz} .
$$
$f_{D_{I2} |(x_0 , y_r )}(x)$ 以及 $f_{D_{I4} |(x_0 , y_r )}(y)$ 的推导与 $f_{D_{I1} |(x_0 , y_r )}(x)$ 和 $f_{D_{I3} |(x_0 , y_r )}(y)$ 类似,其表达式如(39)所示。
$$
f_{D_{I2} |( x_0 , y_r )}( x)= \frac{\beta(-\sqrt{x^2 - y_r^2})}{\int_{x_0-2r_E}^{x_0-r_E} \beta(z)dz} ,
$$
$$
f_{D_{I4} |( x_0 , y_r )}(y)=
\frac{\beta(y_r - y)}{\int_{-\sqrt{4r_E^2-x_0^2}}^{-\sqrt{r_E^2-x_0^2}} \beta(z)dz} .
$$
2) 信干噪比累积分布函数和服务质量度量
Ik的干扰功率 $P_{Ik}$在 R处接收到的累积分布函数和概率密度函数可以表示为
$$
F_{P_{I1} |(x_0,y_r)}(x)= P(P_{I1} \leq x|(x_0, y_r))
= \int_{t’=0}^{x}\int_{t=\sqrt{(r_E+x_0)^2+y_r^2}}^{\sqrt{(2r_E+x_0)^2+y_r^2}} f_{P_r|D_{I1}}(t’)f_{D_{I1} |(x_0,y_r)}(t)dtdt’,
$$
$$
F_{P_{I2} |(x_0,y_r)}(x)= P(P_{I2} \leq x|(x_0, y_r))
= \int_{t’=0}^{x}\int_{t=\sqrt{r_E^2-x_0^2}+y_r}^{\sqrt{4r_E^2-x_0^2}+y_r} f_{P_r|D_{I2}}(t’)f_{D_{I2} |(x_0,y_r)}(t)dtdt’,
$$
$$
F_{P_{I3} |(x_0,y_r)}(y)= P(P_{I3} \leq y|(x_0, y_r))
= \int_{t’=0}^{y}\int_{t=\sqrt{r_E^2-x_0^2}-y_r}^{\sqrt{4r_E^2-x_0^2}-y_r} f_{P_r|D_{I3}}(t’)f_{D_{I3} |(x_0,y_r)}(t)dtdt’,
$$
$$
F_{P_{I4} |(x_0,y_r)}(y)= P(P_{I4} \leq y|(x_0, y_r))
= \int_{t’=0}^{y}\int_{t=\sqrt{r_E^2-x_0^2}+y_r}^{\sqrt{4r_E^2-x_0^2}+y_r} f_{P_r|D_{I4}}(t’)f_{D_{I4} |(x_0,y_r)}(t)dtdt’.
$$
然后,可以使用类似于(29)–(36)的方法获得信干噪比的概率密度函数和累积分布函数:
$$
f_{\text{SINR}|(P_r>P_{th})}(x)= \int_{0}^{r_E} f_{\text{SINR}|(x_0 ,y_r,P_r>P_{th})}(x)f_{D_S}(t)dt,
$$
$$
F_{\text{SINR}|(P_r>P_{th})}(x)= \int_{0}^{x} f_{\text{SINR}|(P_r>P_{th})}(t)dt,
$$
and
$$
f_{D_S}(y)= \frac{y}{\sqrt{y^2 - x_0^2}} \frac{\int_{\sqrt{y^2 -x_0^2}} \beta(t) dt}{\int_{0}^{r_E} \beta(z)dz}.
$$
PRP与标记节点的距离 ds以及ROI内的PRR可以被评估为
$$
\text{PRP}(x_0, y_r, \theta)= P(\text{SINR} \geq \theta|(x_0, y_r)) P(P_r> P_{th})
=(1 - F_{\text{SINR}|(x_0 ,y_r ,P_r >P_{th})}( \theta))
\times(1 -\int_{0}^{P_{th}} f_{P_r |d_s}( x)dx)\times P_{\text{con}|(x_0 , y_r)}
,
$$
$$
P_{\text{con}|d_s} = \exp(-n_\Sigma( x_0 , y_r )) ,
$$
$$
\text{PRR}(d, \theta)=
\frac{\int_{-\sqrt{d^2 -x_0^2}}^{\sqrt{d^2 -x_0^2}} \beta(y)\text{PRP}(x_0, y, \theta)dy}{\int_{-\sqrt{d^2 -x_0^2}}^{\sqrt{d^2 -x_0^2}} \beta(x)dx} ,
x_0 \leq d \leq \sqrt{d_{\text{ROI}}^2 - x_0^2}.
$$
D. 容量推导
链路容量的概率密度函数和期望的解与一维情况相同, (23)–(25)同样适用于二维交叉路口。
IV. NS2仿真与设置
我们采用NS2仿真器版本2.35来验证理论模型。对 NS2源代码进行了一些修改,以调整SINRTs,使用户能够定义SINRTs。此外,我们比较了静态仿真场景和移动性仿真场景的性能,其中移动性交通分别由SUMO和 NS2移动性工具生成。结果表明,在移动场景和静态仿真场景中通过统计得到的性能指标几乎没有差异。因此,在后续NS2仿真实验中,我们采用静态场景仿真来验证理论模型。
A. 灵活的SINR阈值设置
NS2采用基于信干噪比的方法,通过比较信号的信干噪比与存储在modulation table变量中的自定义SINR阈值来确定是否接收到传入信号。SINRT根据调制方式及对应的数据速率(Rd)为固定值,如表I所示。因此,我们通过修改NS2中 WirelessphyExt类的变量类型及其构造函数,重新设计了该类,以支持用户通过可编程的Tcl脚本灵活设置SINRT。具体细节如图4所示。

B. 仿真参数设置
在我们的实验中,我们分别考虑了用于安全消息传播的一维高速公路(长度为5公里)和二维交叉路口道路(每条交叉道路长度为1250米)中的专用短程通信车载自组织网络。网络中的每辆车都具备DSRC能力。车辆呈分段常数密度的泊松分布,其密度是到标记车辆的距离Δ(Δ= x或Δ= y)的函数,如下所示。
$$
\beta(\Delta)= \begin{cases}
1.5\beta_{av} , & -50 \text{m} \leq \Delta \leq 50 \text{m} , \Delta< -100 \text{m} \text{ or } \Delta> 100 \text{m} \
0.5\beta_{av} , & \text{others},
\end{cases}
$$
其中$\beta_{av}$ 分别设置为0.066辆/米、0.132辆/米、0.2车辆/米和 0.5车辆/米。
我们将一维高速公路和二维交叉路口道路的关键仿真参数列于表II中。仿真参数设置与理论计算一致。根据 [35],,传输范围、载波侦测范围和干扰范围的研究均设为300米。载波侦测阈值 $P_{th}$ 通过Nakagami模型计算得出,等于$2.81838\times10^{-11}$瓦特,且接收功率阈值和NS2中的功率监测阈值均设置为 $2.81838\times10^{-11}$瓦特。
C. 车载自组织网络的移动性场景仿真
交通仿真软件SUMO可以模拟车辆以给定速度行驶的真实场景。NS2也提供了一个简单的内置移动模型来驱动节点的移动。我们通过SUMO和NS2的内置移动模型实现了两种移动交通场景。
在SUMO中,我们生成了一个长度为5公里的双车道双向高速公路场景,启用车辆之间的相对速度,每个车道的宽度为3.2米。所有车辆的参数设置如表III所示。每辆车每10毫秒更新一次速度,所有车辆的速度服从均值为 90公里/小时(即25米/秒)、方差为$2 (m/s)^2$的均匀分布。当车辆接近前方车辆的安全距离时,行驶速度会发生变化,从而导致车间距离发生变化,并可近似视为遵循非齐次泊松过程(NHPP)。SUMO以1毫秒采样步长记录车辆位置。在不同时间点由车辆位置生成的日志文件被输入到 NS2程序中,用于仿真移动网络场景。
NS2内置移动模型的移动场景设置为一条长度为6公里的单向右侧行驶高速公路,遵循泊松过程分布且具有分段常数密度的车辆被放置在道路左侧5公里范围内,仿真在5秒内结束。其他参数的使用与SUMO类似。
D. 静态场景仿真与移动场景仿真的比较结果
图5显示了在密度为0.132辆/米时,静态场景仿真和两种移动场景仿真的PRP比较结果。结果表明,在给定接收距离 $d_s$和SINR阈值[10]的情况下,静态场景仿真可以获得与移动场景仿真几乎相同的结果。此外,文献[10]指出,在传输数据包期间,车辆可以被视为静止的。显然,与移动场景仿真相比,静态场景仿真耗时更少,因此我们在接下来的比较中采用静态场景仿真。

V. 理论结果分析与验证
在本节中,我们首先比较理论模型的顺序统计量与无序情况下的时间复杂度。其次,我们在一维以及二维交叉路口场景下对解析模型和 NS2仿真进行了可靠性交叉验证,以保证解析模型的精度。获得了包括PRP、PRR以及不同VANET场景下的信干噪比分布在内的一系列服务质量指标。第三,我们进一步比较了二维和一维两种场景下的PRP。最后,通过数值计算得到了一维和二维车载自组织网络中的链路容量分布。
仿真场景包括一维和两种二维交叉路口场景。具体而言,考虑了两种类型的二维交叉路口场景,因为接收器距离交叉路口越近,产生的干扰就越多。在第一种场景中,假设发送器位于交叉路口,而位于X轴上距离交叉路口 $d_s$处的车辆节点为接收器。在第二种场景中,假设接收器位于交叉路口,而位于负X轴上距离交叉路口 $d_s$处的车辆节点为发送器。所有场景中的不同密度分别为:0.066辆/米作为低密度,0.132辆/米、0.2辆/米作为中等密度,0.5辆/米作为高密度。在每种密度下,我们选择五个值作为 SINRT以观察服务质量度量:23.3 dB (215)、24.9 dB (315)、26.9 dB (500)、28.5 dB (700) 和 30.0 dB (1000)。在NS2仿真中,对相同密度和SINRT的实验重复进行了十次,取十次PRP/PRR的平均值作为PRPs/PRRs的仿真结果。参数设置见第四节。
各种实验的结果为探索所提出模型在一维以及二维车载自组织网络中的精度,以及分析接收距离 $d_s$ 和 SINR阈值对可靠性的影响奠定了基础。
A. 数值分析的时间复杂性
基于顺序统计量和一维高速公路无序情况下的信干噪比分布的计算效率由实验给出。我们采用蒙特卡洛积分和 MPI并行框架来实现数值程序计算PRP,以提高计算速度。这些程序运行在由同构节点组成的MPI集群上。由Intel MPI 5.1.2提供支持。MPI集群中每个节点的硬件包括 Intel E5-2660 2.60 GHz CPU、32 GB内存和20核CPU,用于数值积分。
蒙特卡洛积分需要足够多的采样点以确保精度。采样次数分别为1000次、3000次和5000次。SINR阈值 θ设为 4,信号传播距离 $d_s$设为50米。通过蒙特卡洛积分计算有序和无序情况下单次插值的执行时间分别为38.1328毫秒和736.462毫秒。表IV给出了当采样点数量分别为1000、3000和5000时计算时间和精度的比较结果。从表IV可以明显看出,与无序模型相比,有序模型显著降低了计算复杂度。
B. 理论计算与NS2仿真的交叉验证
1) 信干噪比的概率密度函数、累积分布函数
我们计算了一维场景和两个二维场景中,在干扰范围1500(31.8 dB)内的信干噪比概率密度函数和累积分布函数。图6和图7展示了接收器位于交叉路口时,一维和二维场景中信干噪比的概率密度函数和累积分布函数,对应密度为0.132辆/米。结果表明, $d_s$越小,信干噪比的平均值越大;反之, $d_s$越大,信干噪比的均值越小。较小的 $d_s$值意味着接收器的衰减功率较小,因此信干噪比较大,这与图6和图7的结果一致。


2) 低、中等密度下一维和二维的PRP、PRR
图8–图10 展示了在密度为0.066辆/米和0.132辆/米时,解析模型与 NS2仿真之间的PRPs(成功传输概率)比较结果,分别针对发送器位于交叉路口的一维、二维场景以及接收器位于交叉路口的二维场景。可以看出,在不同密度下,解析结果与仿真结果在各种 $d_s$ 以及SINR阈值条件下均保持一致,同时也表明 $d_s$ 和SINRT影响PRPs。 $d_s$ 从10米开始以20米间隔增至300米,图中明显显示PRPs随 $d_s$ 的增加而下降。随着 $d_s$ 的增加,信道衰减更加严重,导致接收功率降低,从而进一步减小接收器处的信干噪比值,因此无法满足SINR阈值的要求。因此, $d_s$ 的增加必然会导致PRP下降。

另一方面,SINRT越大,解码接收数据包所需的接收功率和信号强度就越强,不满足接收条件的车辆节点将丢弃数据包,导致丢包,因此当SINRT较大(等于 30.0分贝)时,PRP的下降趋势比小值28.5分贝、26.9分贝、24.9分贝和23.3分贝更加明显。图11给出了在一维密度为0.132辆/米的情况下,理论模型与NS2仿真之间的 PRR和PRP对比。结果表明,PRR的数值计算结果与仿真结果接近, $d_s$和SINRT的增加也会导致PRR的下降趋势。




















 890
890

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








