回顾经典，八大算法。

最新推荐文章于 2023-06-28 11:01:37 发布
原创 最新推荐文章于 2023-06-28 11:01:37 发布 · 1.4w 阅读 · 846 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#链表 #数据结构 #spring boot

ssss其实早在一年前，对于八大算法就能1个多小时全部复现出来，起初没觉得有什么，但什么随着力扣刷题，发现八大排序算法越来越重要，因此，我觉得有必要对其进行总结，或许已经有很多人对其总结了，不过总是不如自己亲身经历一遍，再复现一遍，算法重要，思维更重要。

ssss排序的分类：

ssdssss①、内部排序：指将需要处理的所有数据都加载到内部存储器（内存）中进行排序

sdsssss②、外部排序法： 数据量过大，无法全部加载到内存中，需要借助外部存储（文件等）进行排序

ssss而我们所说的方法，都是内部方法。

ssss算法的复杂度：时间复杂度，空间复杂度。
sss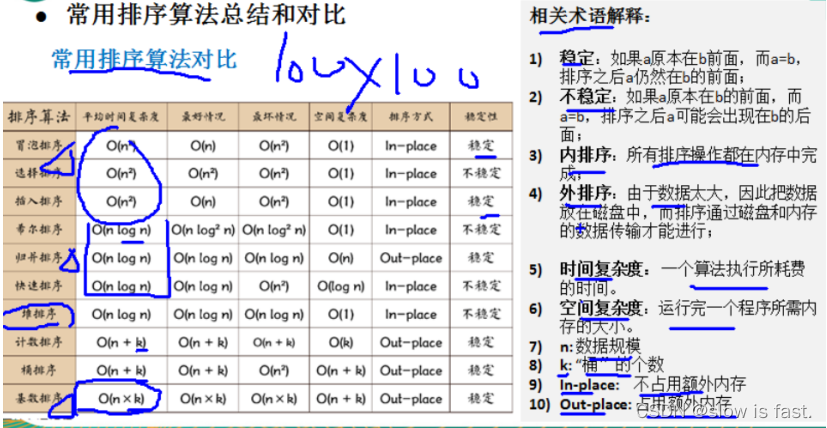在这里插入图片描述

冒泡排序

ssss基本思想：对排序序列进行从前向后（下标较小的开始），依次比较相邻元素的值，若逆序则交换，则值较大的元素逐渐从前移向后，就像水底的气泡。每一轮的排序都是找到一个最大值，放到最后面，就和气泡浮出水面一样，一共需要执行N-1轮

ssss在每一轮过程中，都会比较相邻的大小，如果在某一轮发现都没有进行变化，则表明已经排序好了，所以不需要再继续下去。

sssseg：[35,88,16,27,32,4,90,56,79]
ssasdasdasddsdasdss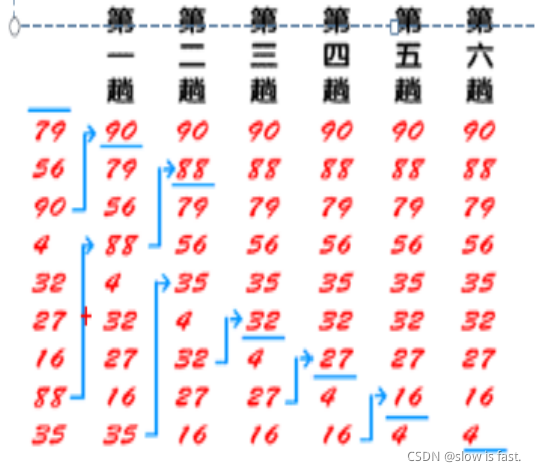在这里插入图片描述

package com.wwj.sort;

import java.util.Arrays;

public class BubbleSort {
    public static void main(String[] args){

        int[] arr = new int[]{35,88,16,27,32,4,90,56,79};
        int tmp;   //中间变量
        boolean flag = false; //标识变量，标识是否进行过交换
        for(int i =0 ; i< arr.length-1 ; i++){
            for(int j=0 ; j<arr.length-1-i; j++){
                if(arr[j] > arr[j+1]){
                    flag = true;
                    tmp = arr[j+1];
                    arr[j+1] = arr[j];
                    arr[j] = tmp;
                }
            }
            //优化
            if(!flag)     //说明依次交换：一次都没有发生过
                break;
            else
                flag = false;  //重置flag！！！，让起进行第二轮的判断，否则就起不到优化的作用了
        }
        System.out.println(Arrays.toString(arr));
    }
}
==================================================================================================================
结果：[4, 16, 27, 32, 35, 56, 79, 88, 90]

选择排序

ssss基本思想：其实和冒泡排序差不多，冒泡排序是一轮一轮的相邻两个进行比较，每一轮可以比较出一个最大值，然后一共要执行N-1次，再次可以通过设置flag,用if语句进行判断。而选择排序是设置一个最小值，一般是初始值设为最小值，然后和所有数值进行比较，找出最小的数值放在第一位，然后依次执行N-1次，每一次比较的元素依次递（可以排成从大到小，也可 以排成从小到大）。
ssasdasddasdd在这里插入图片描述
sssseg：[103，34，119，1]
ssdsdsdsdsdsdss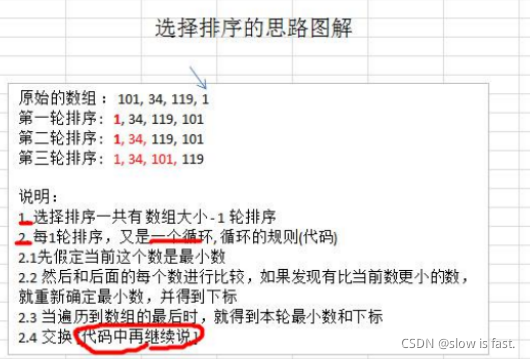在这里插入图片描述

public class selectSort {

    public static void main(String[] args) {
        int[] arr = new int[]{103,34,119,1};
        int minIdx;
        int minVal;
        for(int i=0 ; i< arr.length-1 ; i++){
            minIdx = i;
            minVal = arr[i];
            for(int j=i+1 ; j< arr.length; j++){
                if(minVal>arr[j]){  //记录最大值的下标和值
                    minIdx = j;
                    minVal = arr[j];
                }
            }
            if(minIdx != i){
                arr[minIdx] = arr[i];
                arr[i] = minVal;
            }
        }
        System.out.println(Arrays.toString(arr));
    }
}
==============================================================================================
结果：[1, 34, 103, 119]

插入排序

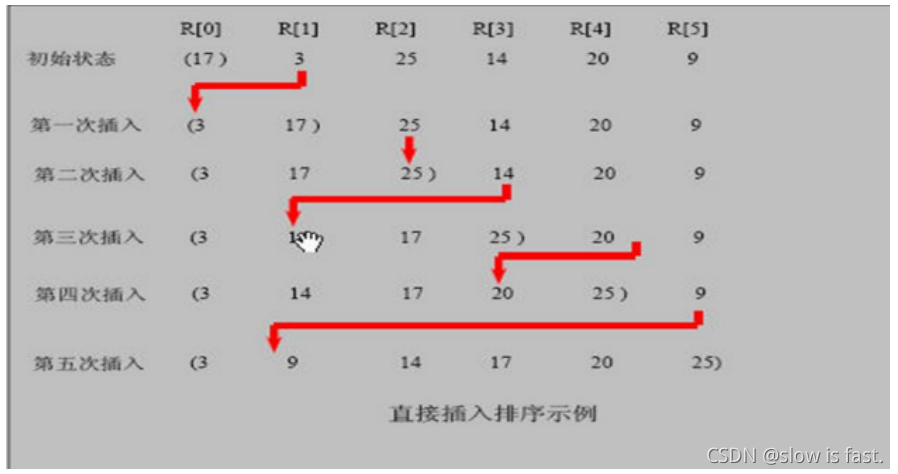
ssss基本思想：将一个数组的元素分成一个有序数组，和无序数组，然后将无序数组的数值依次 和有序数组中得数组（也就是第一个数）进行比较，然后放入到有序数组中，最后也要 执行N-1次。

sssseg：[17，3，25，14，20，9]
在这里插入图片描述

public class insertSort {
    public static void main(String[] args) {

        int[] arr = new int[]{17,3,25,14,20,9};

        int insertIdx;
        int insertVal;
        for(int i=1 ; i<arr.length ; i++){
            insertIdx = i-1;
            insertVal = arr[i];
            while(insertIdx>=0 && insertVal < arr[insertIdx]){
                arr[insertIdx+1] = arr[insertIdx];
                insertIdx--;
            }
            arr[insertIdx+1] = insertVal;
        }
        System.out.println(Arrays.toString(arr));
    }
}
============================================================================================================
结果：[3, 9, 14, 17, 20, 25]

希尔排序

ssss本质：实际上也是一种插入排序，只不过在一个序列中，如果较小得在后面，通过插入排序效率并不高，针对这种情况，提出了希尔排序。

ssss基本思想：首先通过一组元素得基本个数，让其除以2，算出第一次排序得增量是多少，然后分成几个组，对各组进行排序.一直持续到增量为1时结束。而对各组进行排序，我们可以通过交换排序，也可以通过希尔排序，每种排序针对不同得情况。

sssseg：[8，9，1，7，2，3，5，4，6，0]
sadasdasdasdsdasdsadasds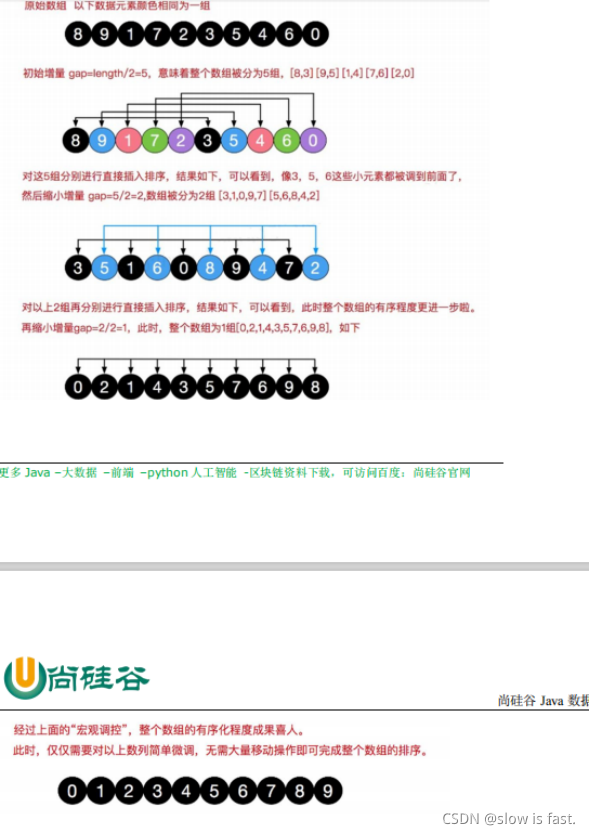在这里插入图片描述
ssss①、希尔+交换

public class shellSort {
    public static void main(String[] args) {
        int[] arr= new int[]{8,9,1,7,2,3,5,4,6,0};
        int temp;
        //1、我们首先要进行分组，然后每组比较，一直分到增量为1时，就结束
        for(int gap = arr.length/2 ; gap>0 ; gap/=2 ){   //增量大小，最大为序列长度的1/2，最小为1，逐半减小

            for(int i = gap ; i<arr.length ; i++){  //交换排序的核心，在下标为增量数gap开始，因为此下标前面正好是有gap个数

                for(int j = i-gap; j>=0 ; j-=gap){   //每次和同组的比较也就是前gap个

                    if(arr[j]>arr[j+gap]){
                        temp = arr[j];
                        arr[j] = arr[j+gap];
                        arr[j+gap] = temp;

                    }
                }
            }
        }
        System.out.println("希尔排序和交换排序后的序列为："+ Arrays.toString(arr));
    }
}
===============================================================================================
结果：希尔排序和交换排序后的序列为[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

ssss②、希尔+插入

public class shellSort {
    public static void main(String[] args) {
        int[] arr= new int[]{8,9,1,7,2,3,5,4,6,0};
        int temp;
        //分组
        for(int gap = arr.length/2 ; gap>0 ; gap/=2){
            for(int i=gap ; i<arr.length ; i++ ){
                //插入排序
                int insertVal = arr[i];
                int insertIdx = i-gap;
                while(insertIdx>=0 && insertVal<arr[insertIdx]){
                    arr[insertIdx+gap] = arr[insertIdx];
                    insertIdx-=gap;
                }
                arr[insertIdx+gap] = insertVal;
            }
        }

        System.out.println("希尔排序和插入排序后的序列为："+ Arrays.toString(arr));
    }
}
===============================================================================================
结果：希尔排序和插入排序后的序列为：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

快速排序

ssss本质：是对冒泡排序的一种改进

ssss基本思想：首先我们要找到他中间索引的值，然后以此分成两个序列，通过编程使左边比右边的数小，然后让两别分别进行递归，这样就达到了排序的效果。

ssss注意：通过while循环找出两边序列各自不符合条件的值，然后交换，但是要考虑：

sdssss1、如果两边全部满足条件呢dsssss2、如果两边有与中间值相等的呢

sssseg：[2,10,8,22,34,5,12,28,21,11]
sdsdsdsssss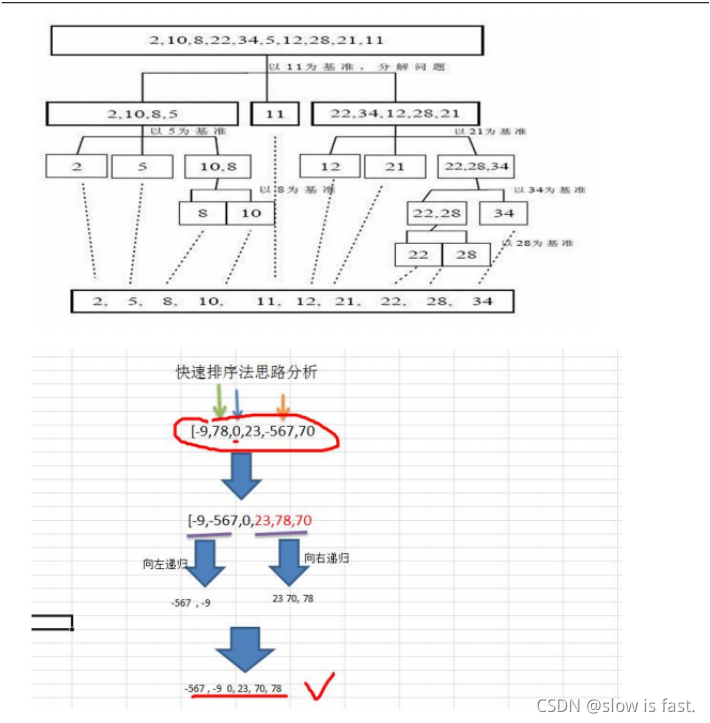在这里插入图片描述

public class quickSort {
    public static void main(String[] args) {
        int[] arr = new int[]{2,10,8,22,34,5,21,21,21,11};
        quickSort(arr, 0 , arr.length-1);
        System.out.println("快速排序"+ Arrays.toString(arr));
    }
    private  static void quickSort(int[] arr ,int left , int right ){  //left，right分别代表序列左右两边的值
        int l = left;
        int r = right;
        int pivot = arr[(l+r)/2];   //中轴值
        int tmp;  //中间值

        //首先我们要以中轴值为界，把序列分成两份，保证左边的序列的数值比右边的序列的数值大
        //首先一个死循环
        while (l<r){
            while(arr[l]<pivot)     l++;    // 以中轴值为界
            while(arr[r]>pivot)     r--;   // 以中轴值为界
            if(l>r)    break;  //如果当l>r时，说明此时左边序列的数字小于右边数列的值

            tmp = arr[l];
            arr[l] = arr[r];
            arr[r] = tmp;    //进行互换，但是要注意，前面两个while循环，都取的是<>号，如果是==呢，此时需要改变l,r的值

            if(arr[l] == pivot)   l++;//交换完后，如果左边相等，我们要让l++,原因：1、以便让后面进行递归，2、退出while循环
            if(arr[r] == pivot)   r--;//交换完成后，如果右边相等，我们要让r--，以便让后面进行递归  2、退出whil循环         }
        }
        //如果是根据后面两个if语句退出的while循环，说明r==f,此时我们为了后面的遍历要r++,f--
        if(r==l){ r+=1;l-=1; }
        //向左递归,但是要判别下最左边的下标小于left<r
        if(left<r)      quickSort(arr,left,r);
        //又向递归，但是要判别下最右边的下标大于f,right>f
        if(right>l)     quickSort(arr,l,right);
    }
}
===============================================================================================
结果快速排序[2, 5, 8, 10, 11, 21, 21, 21, 22, 34]

归并排序

ssss核心思想就是“分治”，“分”的情况比较简单，最后拆成一个元素的序列，“治”的情况比较麻烦，合的时候需要把他们一次一次递归，然后排列。核心为“治”，一共要合并N-1次（N为长度）

ssss分成三个阶段：1、分 2、合 3、复制

sssseg：[2,10,8,22,34,5,21,21,21,11]

public class MergeSort {
    public static void main(String[] args) {
        int arr[] = { 2,10,8,22,34,5,21,21,21,11 };
        int[] tmp = new int[arr.length];
        mergeSort(arr,0,arr.length-1 , tmp);
        System.out.println("归并排序的顺序："+Arrays.toString(arr));

    }
    private static void mergeSort(int[] arr , int left , int right , int[] tmp){
        if(left<right){
            int mid = (left + right)/2;
            mergeSort(arr,left,mid,tmp);
            mergeSort(arr,mid+1,right,tmp);
            merge(arr , left , mid , right ,tmp);
        }
    }
    //合并的方法
    /**
     *
     * @param arr 排序的原始数组
     * @param left 左边有序序列的初始索引
     * @param mid 中间索引
     * @param right 右边索引
     * @param temp 做中转的数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {

        int i = left; // 初始化i, 左边有序序列的初始索引
        int j = mid + 1; //初始化j, 右边有序序列的初始索引
        int t = 0; // 指向temp数组的当前索引
        //(一)
        //先把左右两边(有序)的数据按照规则填充到temp数组
        //直到左右两边的有序序列，有一边处理完毕为止
        while (i <= mid && j <= right) {//继续
            //如果左边的有序序列的当前元素，小于等于右边有序序列的当前元素
            //即将左边的当前元素，填充到 temp数组
            //然后 t++, i++
            if(arr[i] <= arr[j])
                temp[t++] = arr[i++];
            else //反之,将右边有序序列的当前元素，填充到temp数组
                temp[t++] = arr[j++];
        }
        //(二)
        //把有剩余数据的一边的数据依次全部填充到temp
        while( i <= mid)   temp[t++] = arr[i++]; //左边的有序序列还有剩余的元素，就全部填充到temp
        while( j <= right)  temp[t++] = arr[j++]; //右边的有序序列还有剩余的元素，就全部填充到temp
        //(三)
        //将temp数组的元素拷贝到arr
        //注意，并不是每次都拷贝所有
        t = 0;
        int tempLeft = left; //
        //第一次合并 tempLeft = 0 , right = 1 //  tempLeft = 2  right = 3 // tL=0 ri=3
        //最后一次 tempLeft = 0  right = 7
        while(tempLeft <= right) arr[tempLeft++] = temp[t++];
    }
}
==================================================================================================================
结果：归并排序的顺序：[2, 5, 8, 10, 11, 21, 21, 21, 22, 34]

堆排序

ssss基本思想：堆排序分析的比较好的文章在这里插入图片描述

    //堆排序
    public static void heapSort(int[] arr) {
        //构造大根堆
        heapInsert(arr);
        int size = arr.length;
        while (size > 1) {
            //固定最大值
            swap(arr, 0, size - 1);
            size--;
            //构造大根堆
            heapify(arr, 0, size);
 
        }
 
    }
 
    //构造大根堆（通过新插入的数上升）
    public static void heapInsert(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            //当前插入的索引
            int currentIndex = i;
            //父结点索引
            int fatherIndex = (currentIndex - 1) / 2;
            //如果当前插入的值大于其父结点的值,则交换值，并且将索引指向父结点
            //然后继续和上面的父结点值比较，直到不大于父结点，则退出循环
            while (arr[currentIndex] > arr[fatherIndex]) {
                //交换当前结点与父结点的值
                swap(arr, currentIndex, fatherIndex);
                //将当前索引指向父索引
                currentIndex = fatherIndex;
                //重新计算当前索引的父索引
                fatherIndex = (currentIndex - 1) / 2;
            }
        }
    }
    //将剩余的数构造成大根堆（通过顶端的数下降）
    public static void heapify(int[] arr, int index, int size) {
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        while (left < size) {
            int largestIndex;
            //判断孩子中较大的值的索引（要确保右孩子在size范围之内）
            if (arr[left] < arr[right] && right < size) {
                largestIndex = right;
            } else {
                largestIndex = left;
            }
            //比较父结点的值与孩子中较大的值，并确定最大值的索引
            if (arr[index] > arr[largestIndex]) {
                largestIndex = index;
            }
            //如果父结点索引是最大值的索引，那已经是大根堆了，则退出循环
            if (index == largestIndex) {
                break;
            }
            //父结点不是最大值，与孩子中较大的值交换
            swap(arr, largestIndex, index);
            //将索引指向孩子中较大的值的索引
            index = largestIndex;
            //重新计算交换之后的孩子的索引
            left = 2 * index + 1;
            right = 2 * index + 2;
        }
 
    }
    //交换数组中两个元素的值
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

基数排序(桶排序)

ssss之所以叫做桶排序，是因为分成了10个桶，0-9，这样我们可以从这个序列的各个数值的个位开始放入桶中，然后按顺序取出，组成新出的数组，再按照十位……依次类推，需要执行的次数，就是序列中最大数的位数。

ssss基数排序是空间换时间的经典算法

ssss相同的数值排序本来在前面的排序后也在前面
在这里插入图片描述

public class RadixSort {
    public static void main(String[] args) {
        int[] arr = { 53, 3, 542, 748, 14, 214};
        radixSort1(arr); //整体
        System.out.println(Arrays.toString(arr));
    }
    //基数排序，俗称桶排序，基本思想就是：按照个位，十位，百位等分别放入对应得桶中，
    // 然后依次进行排序，所以我们首先要找到一个数组中的最大值，然后用二维数组表达出桶，以及里面对应的数
    private static void radixSort1(int[] arr) {
        int max = arr[0]; //假定第一个数是最大数
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //得到最大数是几位数
        int maxLength = (max + "").length();
        //10  对应0-9. arr.length对应着我们要排序的数组的元素个数，防止溢出
        int[][] bucket = new int[10][arr.length];
        int[] bucketElementCounts = new int[10];    //存入的是特定位是0~9的个数
        for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
            //(针对每个元素的对应位进行排序处理)， 第一次是个位，第二次是十位，第三次是百位..
            for (int j = 0; j < arr.length; j++) {
                //取出每个元素的对应位的值
                int digitOfElement = arr[j] / n % 10;
                //放入到对应的桶中
                bucket[digitOfElement][bucketElementCounts[digitOfElement]++] = arr[j];
            }
            //按照这个桶的顺序(一维数组的下标依次取出数据，放入原来数组)
            int index = 0;
            //遍历每一桶，并将桶中是数据，放入到原数组
            for (int k = 0; k < bucketElementCounts.length; k++) {
                //如果桶中，有数据，我们才放入到原数组
                if (bucketElementCounts[k] != 0) {
                    //循环该桶即第k个桶(即第k个一维数组), 放入
                    for (int l = 0; l < bucketElementCounts[k]; l++) {
                        //取出元素放入到arr
                        arr[index++] = bucket[k][l];
                    }
                }
                //第i+1轮处理后，需要将每个 bucketElementCounts[k] = 0 ！！！！
                bucketElementCounts[k] = 0;
            }
            System.out.println("第" + (i + 1) + "轮，对个/十/百/...位的排序处理 arr =" + Arrays.toString(arr));
        }
    }
}
==============================================================================================================
结果：
第1轮，对个/十/百/...位的排序处理 arr =[542, 53, 3, 14, 214, 748]
第2轮，对个/十/百/...位的排序处理 arr =[3, 14, 214, 542, 748, 53]
第3轮，对个/十/百/...位的排序处理 arr =[3, 14, 53, 214, 542, 748]
[3, 14, 53, 214, 542, 748]
夜深人静写算法（八）- 二分图最大匹配
英雄哪里出来
01-16 8万+
基于深度优先搜索的匹配算法---二分图最大匹配
常用排序算法
南飞的孤雁
09-12 3537
8种常用排序算法
Java实现十大经典排序算法--上
记录一只菜鸡的成长之路
09-13 206
文章目录一、冒泡排序二、选择排序三、插入排序四、希尔排序五、归并排序 一、冒泡排序 算法描述： 冒泡排序，就是从头开始不断比较只要不符合大小关系就交换，每次都可以排好一位，算法动图看起来就像是冒泡一样，所以被称为冒泡排序 代码样例： public static void sort(int[] list) { int n; for (int i = 0; i < list.length; i++) { for (int j = 0; j < list.length-1-i; j++) {
八大算法详细讲解
春秋繁露
05-16 4011
概述 排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。 我们这里说说八大排序就是内部排序。          当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。    快速排序：是目前基于比较的内部排序中被认为是最好的方法，
八大算法
woshiermingerming的博客
11-21 554
http://blog.youkuaiyun.com/hguisu/article/details/7776068
八大排序算法——（万字图文详解）
Forward♞的博客
06-28 6617
本篇博客将对“直接插入排序”、“希尔排序”、“直接选择排序”、“堆排序”、“冒泡排序”、“快速排序”、“归并排序”、“计数排序”进行详细的解析（算法逻辑、具体实现过程、时间复杂度、稳定性），并附以图片帮助大家更好地理解算法逻辑以及实现每个排序的参考代码。
轻松搞定八大机器学习算法
06-19
本课程通过对课件的精心编排，课程内容的不断打磨，重磅推出机器学习8大经典模型算法，对晦涩难懂的数学公式， 通过图形展示其特点和本质，快速掌握机器学习模型的核心理论，将重点回归到机器学习算法本身。...
互联网大厂高频面试题基本总结回顾（含笔试高频算法整理）
热门推荐
张彦峰的博客
04-03 176万+
1.自我介绍+项目介绍+项目细节/难点提问-------这个主要看个人的经历了，每个人都不一样 2.基础知识点考核---------还是可以去增强自己的，也是这次的主要的一些总结思路 3.算法题-----------一般都是LeetCode高频题，这个得在找工作之前的好好的练习(d对常见的高频题进行总结分析，见对应的链接提示)
基于Java编程语言的日常刷题技巧与算法设计源码回顾
最新发布
10-04
例如，回溯算法是一种通过探索所有潜在可能性来找到所有解的算法，它适用于解决组合问题和排列问题，如八皇后问题、子集和问题等。动态规划是一种将复杂问题分解成更小的子问题来解决的算法，它主要应用于具有重叠子...
一站式掌握机器学习八大核心算法
- 本课程通过精心编排的课件和内容，帮助学习者理解和掌握机器学习的八大经典模型算法。 - 课程注重讲解算法的核心理论和实际应用，而非过分深入复杂的数学公式推导。 - 课程内容涵盖了以下八大模型：线性回归、...
八大排序经典算法（图解+参考源代码）
zhongwen7710的专栏
09-11 8621
概述 排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。 我们这里说说八大排序就是内部排序。          当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。    快速排序：是目前基于比较的内部排序中被认为是最好的方法，
八大算法（排序）
柒七的博客
02-19 138
https://www.jianshu.com/p/7d037c332a9d?utm_campaign=hugo&utm_medium=reader_share&utm_content=note&utm_source=weixin-friends 八大排序，三大查找是《数据结构》当中非常基础的知识点，在这里为了复习顺带总结了一下常见的八种排序算法。 常见的八大排序算法，他们之间关系如下： 排序算法.png 他们的性能比较： 性能比较.png 下面，利用Python..
八大常见算法
wangxiaojia42121的博客
04-19 550
概述 排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。 我们这里说说八大排序就是内部排序。          当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。    快速排序：是目前基于比较的内部排序中被认为是最好的方法，
八大排序算法
46426906的博客
11-12 1425
冒泡排序(Bubble Sorting）的基本思想是：通过对待排序序列从前向后（从下标较小的元素开始）,依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就象水底下的气泡一样逐渐向上冒。因为排序的过程中，各元素不断接近自己的位置，如果一趟比较下来没有进行过交换，就说明序列有序，因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。稳定:如果a原本在b前面，而a=b，排序之后a仍然在b的前面;
八大排序算法总结与java实现
Mlib
07-30 1万+
原文链接： 八大排序算法总结与java实现 - iTimeTraveler 概述因为健忘，加上对各种排序算法理解不深刻，过段时间面对排序就蒙了。所以决定对我们常见的这几种排序算法进行统一总结，强行学习。首先罗列一下常见的十大排序算法： 直接插入排序 希尔排序 简单选择排序 堆排序 冒泡排序 快速排序 归并排序 基数排序 其中我们讨论的这八大排序算法的实现可以参考我的Github：SortAlgori
算法之八大排序算法
sixingmiyi39473的博客
02-27 920
1、直接插入排序 插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。 public static void InsertSort(int[] array){ if(array == null || array.length == 0) return ; ...
8大算法详解
chenglc1612的博客
11-22 226
8大算法详解 概述 排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。 我们这里说说八大排序就是内部排序。 当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。 快速排序：是目前...
八大算法总结
大数据精读周刊
04-23 1577
文章目录算法稳定性插入排序直接插入排序折半插入排序希尔排序交换排序冒泡排序快速排序选择类排序简单选择排序堆排序归并排序基数排序外部排序 算法 稳定性 选择排序、快速排序、希尔排序、堆排序不是稳定的排序算法， 冒泡排序、插入排序、归并排序、基数排序是稳定的排序算法 插入排序 有一个已经 有序 的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序，这个时候就要用到一种新的排序方法——插入排序法，插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、
评论 11
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值