读取和分析mirror文件夹下的所有文件,并找到所有的超链接,构造邻接表,然后将该表转换为邻接矩阵,求解GoogleMatrix,最后求出所需解。
每一个超链接对象URL包含下列属性:
Class URL {
Int id;
String url;
Int outDegree = 0
URL next; // 构成链,组成链的所有对象有相同的父URL
}
同1检索文件,并将文件的URL对象插入ArrayList容器中(排重),然后对该文件一行一行分析,找到超链接,并构造URL对象。对该URL,如果ArrayList容器中没有由它构造的对象,插入容器,否则不插。同时找到该URL的父URL对象,将其插入父对象所对应的链表,并将父对象的出度outDegree加1。
while((line = br.readLine())!=null) {
if(line.contains("a href")) {
subLine = line.split("\"");
for(int j = 0; j < subLine.length - 1; j++) {
if(subLine[j].contains("a href")) {
hyperLink = subLine[j+1];
id = findIdInTableHead(hyperLink);
URL linkURL =new URL(hyperLink, id);
if(id ==tableHead.size()) {
tableHead.add(new URL(hyperLink, id));
}
URL tmpURL = parentURL;
while(tmpURL.getNext() !=null) {
tmpURL = tmpURL.getNext();
}
tmpURL.setNext(linkURL);
parentURL.modifyOutDegree();
}
}
}
构造完邻接表后,将其转化为邻接矩阵,遍历ArrayList容器中每个元素的链表,检查链表中每个URL对象的id值,修改矩阵中对应的元素,求出矩阵L和其转置矩阵,最后求出GoogleMatrix。
double[][] L =newdouble[tableHead.size()][tableHead.size()];
double[][] lTransport =newdouble[tableHead.size()][tableHead.size()];
URL tailURL = null;
for(int i = 0; i <tableHead.size(); i ++) {
tailURL = tableHead.get(i);
if(tailURL.getNext() ==null) {
for(int j = 0; j <tableHead.size(); j++) {
L[i][j] = 1.0/tableHead.size();
}
} else {
while(tailURL.getNext() !=null) {
L[i][tailURL.getId()] = 1.0 /tableHead.get(i).getOutDegree();
tailURL = tailURL.getNext();
}
}
}
for(int i = 0; i <tableHead.size(); i++) {
for(int j = 0; j <tableHead.size(); j++) {
lTransport[i][j] = L[j][i];
}
}
googleMatrix =newdouble[tableHead.size()][tableHead.size()];
for(int i = 0; i <tableHead.size(); i++) {
for(int j = 0; j <tableHead.size(); j++) {
googleMatrix[i][j] = (1 -beta) * lTransport[i][j];
if(i == j) {
googleMatrix[i][j] +=beta / tableHead.size();
}
}
}
求解pageRank, 该算法的基本想法是,互联网上每一个页面看做一个节点,不同页面之间的连接关系看做是有向边,从而得到当前互联网的网络拓扑结构。在这样一个网络拓扑结构中,每一个节点都有一个评分。如果从A到B存在一条边,则如果A的评分高,则B的评分相应的也比较高。这样存在一个评分动态传递的过程,也就是如果A的评分为score,A的外链数位n,则通过每一条外链传递的评分就为score/n,如果B是A的链出节点,则B从A中获得score/n的评分。用严格的数学公式表达如下:
其中,R(i)表示节点i的page rank评分,B(i)为指向i的节点集合,N(j)表示j的外链个数。C为一个给定常数。
根据PageRank求解公式
p = newdouble[tableHead.size()];
double[] pTmp =newdouble[p.length];
double sum = 0;
for(int i = 0; i <p.length; i++) {
p[i] = 1.0 /tableHead.size();
pTmp[i] = p[i];
}
for(int number = 0; number < 50; number++) {
for(int i = 0; i <p.length; i ++) {
sum = 0;
for(int j = 0; j <p.length; j++) {
sum += lTransport[i][j] * pTmp[j];
p[j] = sum;
}
for(int j = 0; j <p.length; j++) {
p[i] = 1.0 /tableHead.size();
pTmp[i] = p[i];
}
}
}
最后对PageRank值数组p排序,求出 top 10 的值。







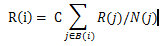
















 1549
1549

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








