首先定义一个原始最优化问题:

引入广义拉格朗日函数,将约束问题转换为无约束优化问题:
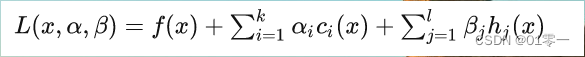
参数和自变量x求偏导,分别为零,就能解出一个值(极大值或者极小值)。
直接求解有时候非常困难,转化为它的等价的或者近似的新问题,这个新问题就叫做对偶问题。
约定:
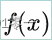 的凹凸性不确定
的凹凸性不确定- 最优结果表示为

一般地,拉格朗日对偶问题有以下两个优点:
- 约束条件比原问题更少
- 一定是凹函数
定义拉格朗日对偶函数:
不管原函数地凹凸性如何,它的对偶函数一定是凹函数。
对偶函数和原函数的关系:

即对偶函数的值不会超过原函数的最优值。
我们已经知道对偶函数的值总是小于原函数的最值,如果能找到对偶函数的最大值,也就找到了对偶函数中最能近似原函数的解,对偶函数是原函数的下界。























 9012
9012

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








