归并排序及其应用 c++实现

归并排序是基于分治的思想，分治策略：将原问题划分为n个规模较小的并且结构与原问题相似的子问题，递归的解决这些子问题，然后合并其结果，得到的就是原问题的解了。
分治的模式在每一层的递归上都有三个步骤：
1、 分解：将原问题分解为一系列的子问题
2、 解决: 递归的解决各个子问题。若子问题足够的小，则直接求解。
3、 合并：将子问题的结果合并，变为原问题的解。

归并算法完全依照于分治的策略：
1、 分解：将n个元素分成含有n/2个元素的子序列
2、 解决：用合并排序法将两个自序列递归的进行排序
3、 合并：合并俩个已经排序的自序列得到排序的结果。
在对自序列进行排序的时候，其长度为1的时候，表示已经排序完成，作为递归出口！
具体的过程如下图：

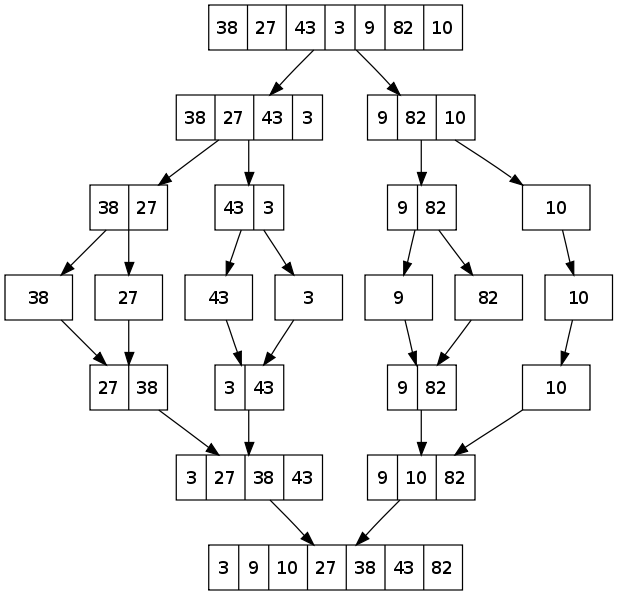
归并排序的前两步骤是很好做的，分解就是二分的思想，解决就是递归到自序列为1，根据这个已经排好序的自序列向上递归！
现在最重要的第三步，合并!要怎么合并呢？
算法设计这选择的方法是引入一个临时数组，把已经排好序的两个自序列一次比较其中最小，将最小的加入临时数组，如下图：
最开始如下图：

然后经过把左边数组中的最小的加入临时数组，如下图：

经过若干次的步骤之后变为：

接着就是在临时数组中保存的是已经把左右两边的子序列排好序的数组了！
合并的过程如下：

void Merge(int l,int m,int r)
{
    int i=l,k=l,j=m+1;
    while(i<=m && j<=r) {
        if(A[i]>A[j]) T[k++] = A[j++];
        else T[k++] = A[i++];
    }
    while(i<=m) T[k++] = A[i++];
    while(j<=r) T[k++] = A[j++];
    for(i=l;i<=r;i++) A[i] = T[i];
}

下面是递归的过程：

void mergesort(int l,int r)
{
    if(l>=r) return ;
    int mid = (l+r)>>1;
    mergesort(l,mid);
    mergesort(mid+1,r);
    Merge(l,mid,r);
}

所有代码如下：

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int MX = 1e6 +5;
int T[MX],t[MX];
int A[MX];
void Merge(int l,int m,int r)
{
    int i=l,k=l,j=m+1;
    while(i<=m && j<=r) {
        if(A[i]>A[j]) T[k++] = A[j++];
        else T[k++] = A[i++];
    }
    while(i<=m) T[k++] = A[i++];
    while(j<=r) T[k++] = A[j++];
    for(i=l;i<=r;i++) A[i] = T[i];
}
void mergesort(int l,int r)
{
    if(l>=r) return ;
    int mid = (l+r)>>1;
    mergesort(l,mid);
    mergesort(mid+1,r);
    Merge(l,mid,r);
}
int main(void)
{
    int N;freopen("in.txt","r",stdin);
    cin>>N;
    for(int i=0;i<N;i++) cin>>A[i];
    mergesort(0,N-1);
    for(int i=0;i<N;i++) cout<<A[i]<<endl;
    return 0;
}

然后还看到《算法入门经典》的归并排序，基本的思想是一样的，就是把所有的过程合并到一个函数里面：

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int MX = 1e6  + 5;
int A[MX],tmp[MX];

void mergesort(int A[],int l,int r,int *t)
{
    if( (r-l)<=1) return ;
    int mid = l+(r-l)>>1;
    mergesort(A,l,mid,t);
    mergesort(A,mid+1,r,t);
    int k=l,p = l,q = mid+1;
    while(p<=mid  || q<=r) {
        if(q>r || (p<=mid&&A[p]<=A[q]) ) t[k++] =  A[p++];
        else t[k++] =  A[q++];
    }
    for(int i=l;i<=r;i++) A[i] = t[i];
}
int main()
{
    int N;freopen("in.txt","r",stdin);
    memset(tmp,0,sizeof tmp);
    cin>>N;
    for(int i=0;i<N;i++) cin>>A[i];
    mergesort(A,0,N-1,tmp);
    for(int i=0;i<N;i++)  cout<<A[i]<<endl;;
    return 0;
}

归并排序的应用

归并排序求逆序数，
在归并排序的过程中是将数组划分为两半，对应于两个数组合并的时候进行比较，如果A[i]>=A[j]的时候我们不仅任何操作，如果A[i]

AC代码

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int MX = 1000+5;
int A[MX], t[MX];
int ans;
void Merge(int l,int m,int r)
{
    int i=l,j= m+1,k=l;
    while(i<=m && j<=r) {
        if(A[i]>A[j]) {
            t[k++] = A[j++];
            ans+=m-i+1;
        } else t[k++]  = A[i++];
    }
    while(i<=m) t[k++] = A[i++];
    while(j<=r) t[k++] = A[j++];
    for(i=l;i<=r;i++) A[i] = t[i];
}
void mergesort(int l,int r)
{
    if(l>=r) return ;
    int mid = (l+r)>>1;
    mergesort(l,mid);
    mergesort(mid+1,r);
    Merge(l,mid,r);
}
int main(void)
{
    int _;
    int N;//freopen("in.txt","r",stdin);
    cin>>_;
    for(int cas=1;cas<=_;cas++) {
        cin>>N;ans = 0;
        for(int i=0;i<N;i++) cin>>A[i];
        mergesort(0,N-1);
        printf("Scenario #%d:\n%d\n\n",cas,ans);
    }
    return 0;
}