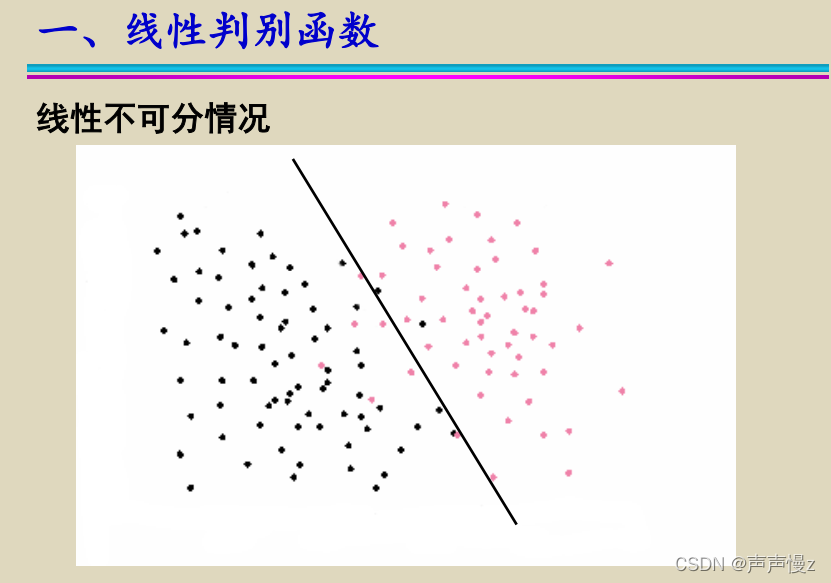
线性分类器-机器学习

二分类问题

直接假设判别函数具有某种形式,然后利用样本集确定出判别函数中的未知参数。
𝑔(𝑥)的具体形式需根据样本集在模式空间中的分布情况或相关领域的专业知识来确定。
本章研究𝑔(𝑥)为线性函数时,分类器参数的估计问题。

基于样本的直接确定判别函数方法：

如何估计这些未知参数？
（1）应针对不同的实际情况，提出不同的设计要求，使得所设计的分类器尽可能好地满足这些要求。
（2） 由于所提要求不同，结果也相各异，这说明上述“尽可能好”是相对于所提要求而言的。

这种设计要求，往往用某个特定的函数来表达，称之为准则函数,“尽可能好”的结果对应于准则函数取最优值。

虽然不知道上面那段估计未知参数的文字是什么意思，反正最后就是用函数来作为准则函数就行，然后用函数去分类

分类器设计问题就转化为求准则函数极值的问题了，因此就可以利用最优化技术解决模式分类问题。

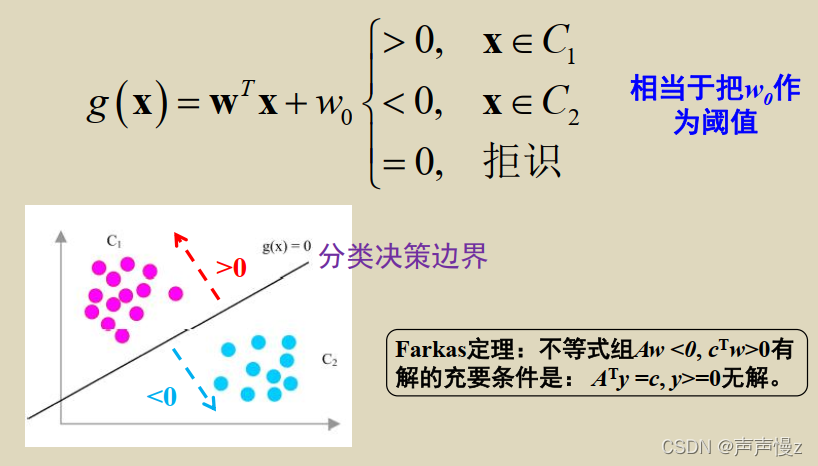
线性判别函数

上面两个形式是等价的
$w_0$是形式一的阈值。

二分类问题的决策规则：



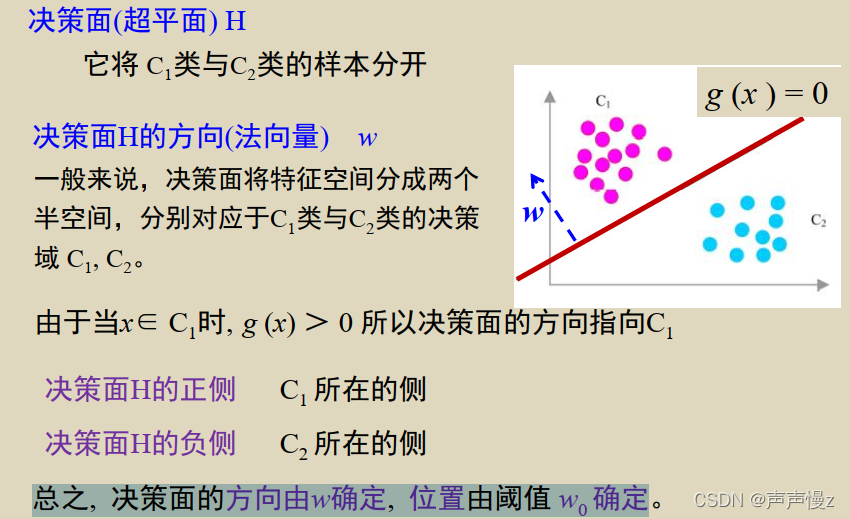
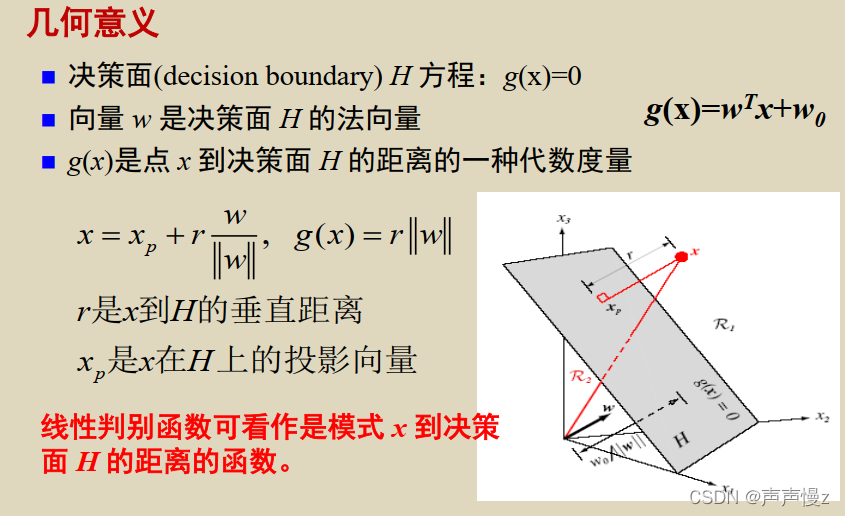
$g(x)$是点x到决策面$H$的距离的一种代数度量。

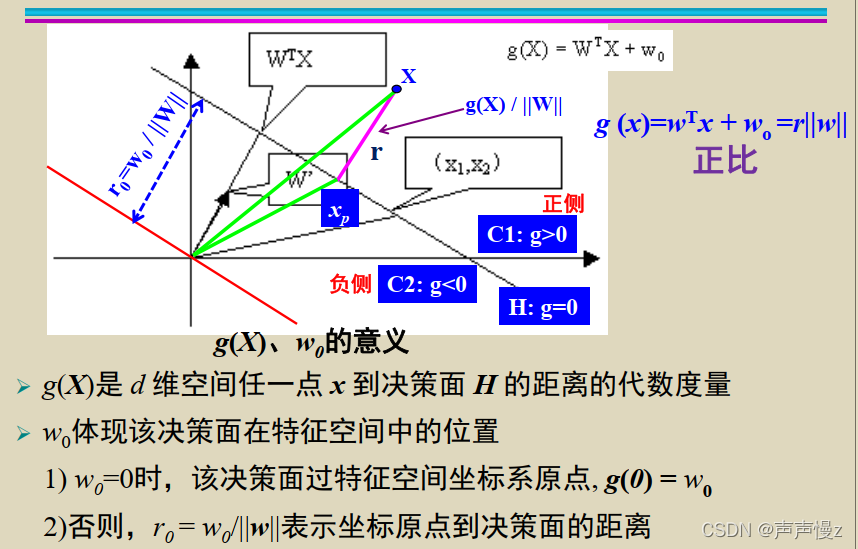
$w_0$体现该决策面在特征空间中的位置

1. $w_0=0$时，该决策面过特征空间坐标系原点, $g(0)=w_0$
   2)否则， $r_0=w_0/||w||$表示坐标原点到决策面的距离。

线性分类器设计的主要步骤

所谓设计线性分类器， 就是利用训练样本集建立线性判别函数。
（1） 估计其中未知参数$w$和 $w_o$， 即寻找最好参数的过程。
（2）最好的参数往往是准则函数的极值点。
（3）转化为利用训练样本集寻找准则函数的极值点$w$和 $w_o$ 的问题。

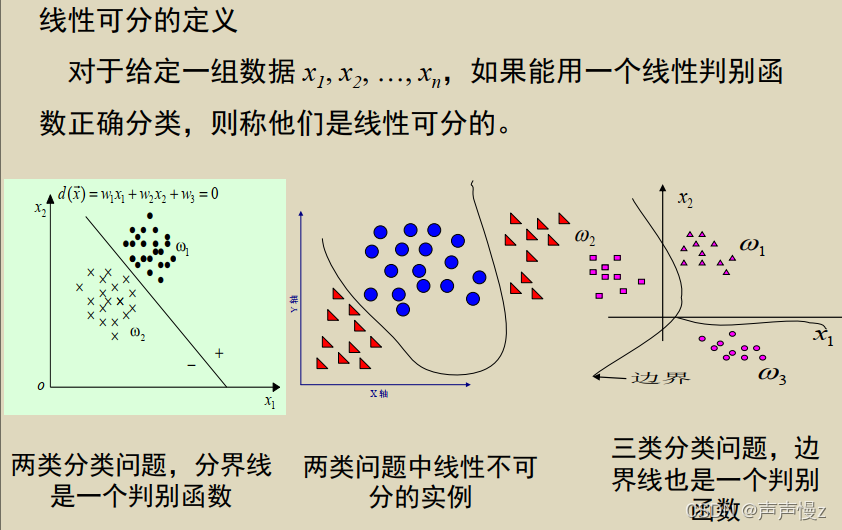
分类决策问题

1. 分类的基本原理
   不同模式对应特征点在不同的区域中散布。运用已知类别的训练样本进行学习，产生若干个代数界面 $g(x)=0$，将特征空间划分成一些互不重叠的子区域。
2. 判别函数表示界面的函数 g(x) 称为判别函数（Discriminant Function） 。
   

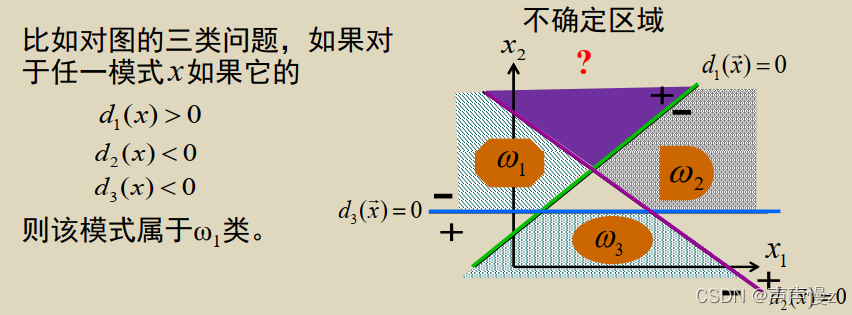
多类决策问题

多分类学习方法：

一对其余

线性判别函数将属于${\omega }_i$类的模式与其余不属于${\omega }_i$类的模式分开，$m$类分类问题转换成$m-1$个两类问题。 $m$类问题要有$m$个判别函数 $d_i，i=1,2,\dots ,m$。
判别规则：
$$\{\begin{array}{l}{d}_i(x)>0\\ d_j(x)\le 0\forall j\ne i\end{array}$$

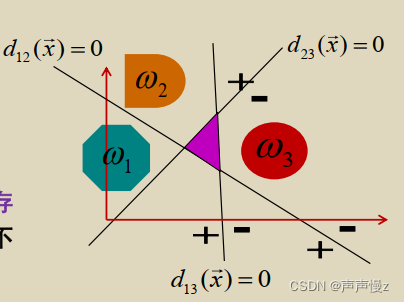
一对一

对m类中的任意两类${\omega }_i$和${\omega }_j$都分别建立一个判别函数，这个判别函数将属于${\omega }_i$类与${\omega }_j$类的模式区分开，此函数对其他分类不提供信息，因此， $m$类问题需要建立$m(m-1)/2$ 个判别函数$d_{ij},i=1,2,\dots ,m$

判别规则为：
若$d_{ij}(x)>0，j\ne ij=1,2,\dots ,m$则判x属于${\omega }_i$

采用这种方案，判别空间中同样可能存在不确定区域，如图中的斜线区域。不确定区域中的模式无法确定其类别。

多对多

m类问题定义m个判别函数 $d_i，i＝1,2,\dots ,m$。

判别规则为: 若$d{i}_{(}x)>d_j(x),j\ne i;i,j＝1,2,\dots ,m$则判$x$属于${\omega }_i$类。

决策面$H_{ij}$方程为$d_i(x)=d_j(x)j\ne i;i,j＝1,2,\dots ,m$

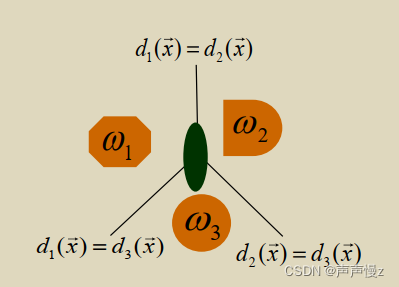
总结

最小距离准则

d 维空间中两个向量之间的欧氏距离
设 $x=(x_1,x_2,\dots ,x_d{)}^T,y=(y_1,y_2,\dots ,y_d{)}^T$，则x, y之间的欧氏距离$d$为 $d^2=(x-y{)}^T(x-y)$。

同类模式在模式空间中应相互靠近，根据这一特点, 我们可利用距离最小准则来设计分类器。

设有m类已知类别的模式(样本)集。计算${\omega }_i$类中所有样本的均值 ${\mu }_i$,记样本 $x$ 到 ${\omega }_i$ 类的距离为：$d_i(x)=(x-{\mu }_i{)}^T(x-{\mu }_i),i=1,2,\dots ,m$。

按最小距离分类原理，决策规则为：
若$D_i(x)<D_j(x),j\ne i;i,j=1,2,\dots ,m$则判x属于${\omega }_i$类。
就是离那里近归为哪里。

分类效果不好的原因在于判别函数的权向量及阈值仅仅利用了各类样本的均值信息，而没有充分利用样本的其它信息。

感知器准则

基本概念

(1) 线性可分性及其概率

假设已知一组容量为n的样本集$y_1,y_2,\dots ,y_n$， 其中$y_i$为$d’$维增广样本向量， 分别来自${\omega }_1$类和${\omega }_2$类。 如果存在一个权向量$w$， 使得对于任何 $y\in {\omega }_1$， 都有 $w^{T}y>0$,而对于任何$y\in {\omega }_2$， 都有都有$w^{T}y<0$， 则称这组样本集为线性可分的， 否则为线性不可分。

总结，就是对于${\omega }_1$类$w^{T}y>0$，对于${\omega }_2$类$w^{T}y<0$

反过来，如果样本集是线性可分的，则必存在一个权向量$w$，能将这个样本集正确的分类。

(2) 样本的规范化

如果样本集$y_1,y_2,\dots ,y_n$是线性可分的，则必存在某个或某些权向量$w$，使得：
$$\{\begin{array}{l}{w}^T{y}_i>0,y_i\in {\omega }_1\\ w^T{y}_i<0,y_i\in {\omega }_2\end{array}$$
如果在来自${\omega }_2$类的样本$y_j$ 前面加上一个负号，即令$y_j^{’}=-y_j$，其中$y_j\in {\omega }_2$，则有$w^T{y}_j^{’}>0$。因此，令
$$y_n^{’}=\{\begin{array}{l}{y}_i,对于一切y_i\in {\omega }_1\\ -y_j,对于一切y_j\in {\omega }_2\end{array}$$
上述过程称为样本的规范化， $y_n^{’}$ 叫做规范化增广样本向量。

上面这段话的意思大概是，把原本需要用$w^T{y}_i$判别的样本集，现在简单地根据符号的正负便能判断相应的样例是属于${\omega }_1$还是${\omega }_2$

(3)解向量和解区

在线性可分情况下，满足$w^T{y}_i>0,i=1,2,\dots ,n$ 的权向量$w$称为解向量。
方程$w^T{y}_i=y_i^{T}w=0$确定了一个以yi为法向量的超平面， $n$个样本将产生$n$个超平面，每个超平面把权空间分为两个半空间,且$w$位于正半空间。 解向量若存在，必在 $n$ 个正半空间的交迭区，且该区任意向量都是解向量$w$。可见解向量往往不只一个，而是无穷多个解向量组成的区域，称之为解区。

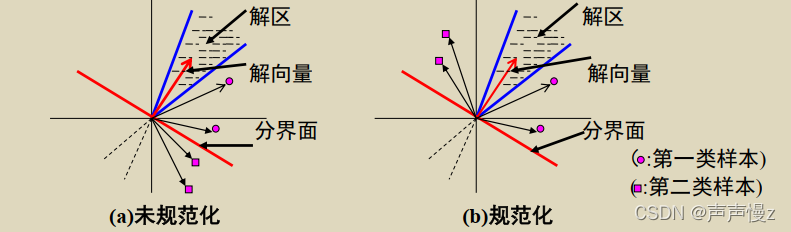
(4)对解区的限制

对解区加以限制的目的在于使解向量$w$更可靠。通常认为，越靠近解区中心的解向量，似乎越能对新的样本正确分类。
因此，引入余量$b>0$，并寻找满足$w^T{y}_i\ge b$的解向量。显然，由$w^T{y}_i\ge b>0$所产生的正半空间的交迭区(即新解区)位于原解区之中。
它的边界离开原解区边界的距离为$b/||yi||$。如图所示。

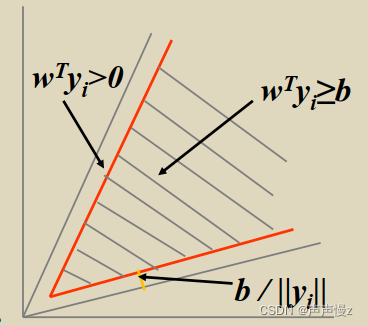
引入余量的目的是使解向量𝑤不至于解区的边界点上。

感知器准则函数

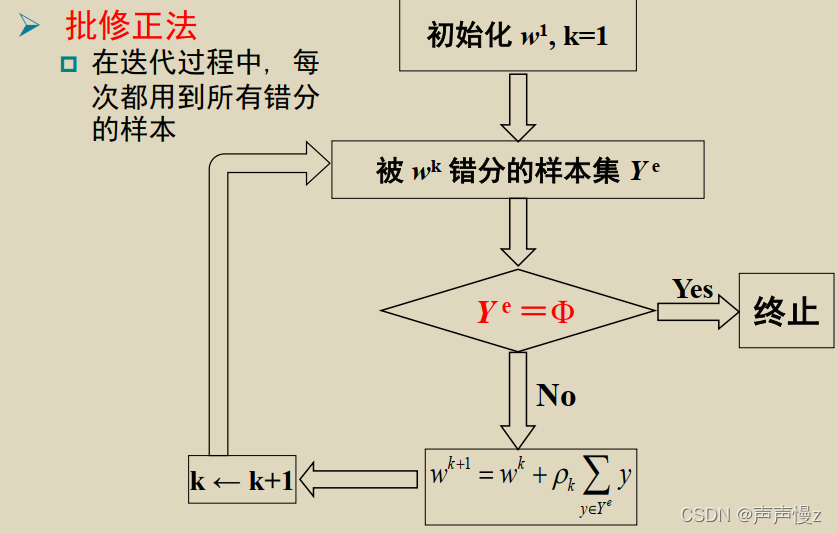
注意事项：
（1）$y_i$是规范化增广样本，所以$w^T{y}_i>0$，所以当 $y$ 被错分类时 $w^{T}y\le 0$,即 $-w^{T}y\ge 0$。
（2）准则函数是根据被错分的样本来计算的

最小平方误差准则

由于感知器准则及其梯度下降算法只适用于线性可分情况，对于线性不可分情况，迭代过程永远不会终结，即算法不收敛，实际问题事先无法确定是否线性可分。
所以希望得到一种对两种情况都可适用的线性判别算法：
➢ 对线性可分问题，可得到一个如感知器准则函数那样的解向量；
➢ 对线性不可分问题，能够得到一个使某种度量误差（或损失）的准则函数达到最小值的解向量。

最小平方误差准则函数