本文详细介绍了Go语言中的浮点数类型（float32、float64）及其精度问题，包括类型声明、精度损失、打印精度、科学计数法和比较大小。同时，还探讨了复数类型（complex64、complex128），包括创建、运算及比较。文章以实例展示了浮点数和复数的使用，强调了在处理浮点数时需要注意的精度问题和正确比较方式。
目录
1. 浮点型
| 序号 | 类型和描述 | 特性 |
|---|---|---|
| 1 | float32 IEEE-754 32位浮点型数 | a.占用4个字节内存 b.精度比float64低 c.有时候也叫单精度类型 |
| 2 | float64 IEEE-754 64位浮点型数 | a.占用8个字节内存 b.默认是64位的浮点类型（float64） c.某些编程语言把这种类型称为双精度类型（double） |
| 3 | complex64 32 位实数和虚数 | 由两个 float32 类型的值分别表示复数的实数部分和虚数部分 |
| 4 | complex128 64 位实数和虚数 | 由两个 float64 类型的值分别表示复数的实数部分和虚数部分 |
2. 类型声明
package main
import "fmt"
func main() {
// 声明浮点类型变量
// float可以表示正数或负数
var num1 float32 = -12.345
var num2 float64 = 12.345
fmt.Println(num1) // -12.345
fmt.Println(num2) // 12.345
// 以下三种声明方式均是等价的
// 只要数字含有小数部分，那么它的类型默认是float64
var num3 float64 = 3.1415
num4 := 3.1415
var num5 = 3.1415
fmt.Println(num3) // 3.1415
fmt.Println(num4) // 3.1415
fmt.Println(num5) // 3.1415
fmt.Printf("num5的类型是: %T\n", num5) //num5的类型是: float64
// 如果你使用一个整数来初始化某个变量，那么你必须指定它的类型为float64,否则它就是一个整数类型
var num6 float64 = 42
fmt.Printf("num6 = %f\n", num6) // num6 = 42.000000
fmt.Printf("num6的类型是: %T\n", num6) // num6的类型是: float64
num7 := 2020
fmt.Printf("num7 = %f\n", num7) // num7 = %!f(int=2020)
fmt.Printf("num7的类型是: %T\n", num7) // num7的类型是: int
fmt.Println("num7 = ", num7) // num7 = 2020
// 当你声明变量却不对其进行初始化时，它的值是零
var num8 float64
fmt.Println(num8) // 0
}
3. 精度损失
package main
import (
"fmt"
"strconv"
)
func main() {
// 尾数部分可能丢失，造成精度损失
var num1 float32 = -123.0000901
var num2 float64 = -123.0000901
fmt.Println(num1) // -123.00009
fmt.Println(num2) // -123.0000901
// int32 转 float64 在数值很大的时候出现偏差
var num3 float32 = 80.45
var num4 float64
// 有些函数只能接收float64, 此时只能强转
num4 = float64(num3 )
// 强转后出现偏差
fmt.Println(num3 ) // 80.45
fmt.Println(num4 ) // 80.44999694824219
// 计算造成精度损失
var num5 = 10.2
fmt.Println(num5 * 100) // 1019.9999999999999
// 解决方法
fmt.Println(floatGetnum(num5 * 100)) // 1020
}
func floatGetnum(num float64) float64 {
theNum, _ := strconv.ParseFloat(fmt.Sprintf("%.8f", num), 64)
return theNum
}出现浮点数不精确的原因是，浮点数储存至内存中时，2的-1、-2……-n次方不能精确的表示小数部分，所以再把这个数从地址中取出来进行计算就出现了偏差。
一个 float32 类型的浮点数可以提供大约 6 个十进制数的精度，而 float64 则可以提供约 15 个十进制数的精度，通常应该优先使用 float64 类型，因为 float32 类型的累计计算误差很容易扩散，并且 float32 能精确表示的正整数并不是很大。
4. 打印精度
package main
import "fmt"
func main() {
/* 显示浮点类型 */
// 1.使用Print或Println打印浮点类型时，默认的行为是尽可能多显示几位小数
// 2.如果你不想这样，那么应该使用Printf函数，结合%f格式化动词来指定显示小数的位数
num11 := 21.0 / 5.0
fmt.Println(num11) // 4.2
num12 := 11 / 3
fmt.Println(num12) // 3
/* %f格式化 */
// 它有两部分组成：宽度 + 精度
// 宽度：会显示出的最少字符个数(包含小数点和小数)
// a.如果宽度大于数字的个数，那么左边会填充空格
// b.如果没有指定宽度，那么就按实际的位数进行显示
// 精度：小数点后面显示的位数
num13 := 1.0 / 3
fmt.Println(num13) // 0.3333333333333333
fmt.Printf("v = %v\n", num13) // v = 0.3333333333333333
fmt.Printf("f = %f\n", num13) // f = 0.333333
// %.3f小数点后保留3位
fmt.Printf("f = %.3f\n", num13) // f = 0.333
// %4.2f包含小数点共4位，其中小数点后保留2位
fmt.Printf("42f = %4.2f\n", num13) // 42f = 0.33
// 如果想使用0代替空格作为填充
fmt.Printf("%05.2f\n", num13) // 00.33
}打印格式说明：
%v 值的默认格式表示
%b 无小数部分、二进制指数的科学计数法，如-123456p-78；参见strconv.FormatFloat
%e 科学计数法，如-1234.456e+78
%E 科学计数法，如-1234.456E+78
%f 有小数部分但无指数部分，如123.456
%F 等价于%f
%g 根据实际情况采用%e或%f格式（以获得更简洁、准确的输出）
%G 根据实际情况采用%E或%F格式（以获得更简洁、准确的输出）
%f: 默认宽度，默认精度
%9f 宽度9，默认精度
%.2f 默认宽度，精度2
%9.2f 宽度9，精度2
%9.f 宽度9，精度0
5. 科学计数法
import "fmt"
func main() {
// 浮点数在声明的时候可以只写整数部分或者小数部分
const num1 = .71828
const num2 = 1.
// 很小或很大的数最好用科学计数法书写，通过 e 或 E 来指定指数部分：
const Avogadro = 6.02214129e23 // 阿伏伽德罗常数
const Planck = 6.62606957e-34 // 普朗克常数
fmt.Println(num1) // 0.71828
fmt.Println(num2) // 1
fmt.Println(Avogadro) // 6.02214129e+23
fmt.Println(Planck) // 6.62606957e-34
}
6. 比较大小
package main
import (
"fmt"
"math"
)
func main() {
// 如何比较两个浮点数
num := 0.1
num += 0.2
fmt.Println(num == 0.3) // false
// 正确的做法
fmt.Println(math.Abs(num-0.3) < 0.0001) // true
}
7. 复数
Go提供了两种大小的复数类型：complex64和complex128，分别由float32和float64组成。
package main
import (
"fmt"
"math/cmplx"
)
func main() {
// 内置函数complex从指定的实部和虚部构建复数
var x complex128 = complex(1, 2) // 1+2i
var y complex128 = complex(3, 4) // 3+4i
// 内置函数real和imag用来获取复数的实部和虚部
fmt.Println(x * y) // (-5+10i)
fmt.Println(real(x * y)) // -5
fmt.Println(imag(x * y)) // 10
// 如果一个浮点数的字面量后面跟着一个i，那么它将变成一个复数的虚部，这个复数的实部是0
fmt.Println(2i * 3i) // (-6+0i) , i² = -1
// math/cmplx包提供了操作复数的函数
// 例如求复数的平方根或复数的幂函数
fmt.Println(cmplx.Sqrt(-1)) // (0+1i)
}复数可以通过== 或 !=进行比较。两个复数相等当且仅当它们的实部和虚部都相等(复数底层是浮点数，因此做相等比较的时候要特别小心)。
8. 示例
下面的程序使用comlex128算法来生成Mandelbrot图像：
package main
import (
"fmt"
"image"
"image/color"
"image/png"
"log"
"math/cmplx"
"os"
)
func main() {
const (
xmin, ymin, xmax, ymax = -2, -2, +2, +2
width, height = 1024, 1024
)
// 需要保存的文件
imgcounter := 123
imgfile, _ := os.Create(fmt.Sprintf("%03d.png", imgcounter))
defer imgfile.Close()
// 新建一个 指定大小的 RGBA位图
img := image.NewRGBA(image.Rect(0, 0, width, height))
for py := 0; py < height; py++ {
y := float64(py)/height*(ymax-ymin) + ymin
for px := 0; px < width; px++ {
x := float64(px)/width*(xmax-xmin) + xmin
z := complex(x, y)
// Image point (px, py) represents complex value z.
img.Set(px, py, mandelbrot(z))
}
}
png.Encode(os.Stdout, img) // NOTE: ignoring errors
// 以PNG格式保存文件
err := png.Encode(imgfile, img)
if err != nil {
log.Fatal(err)
}
}
func mandelbrot(z complex128) color.Color {
const iterations = 200
const contrast = 15
var v complex128
for n := uint8(0); n < iterations; n++ {
v = v*v + z
if cmplx.Abs(v) > 2 {
return color.Gray{255 - contrast*n}
}
}
return color.Black
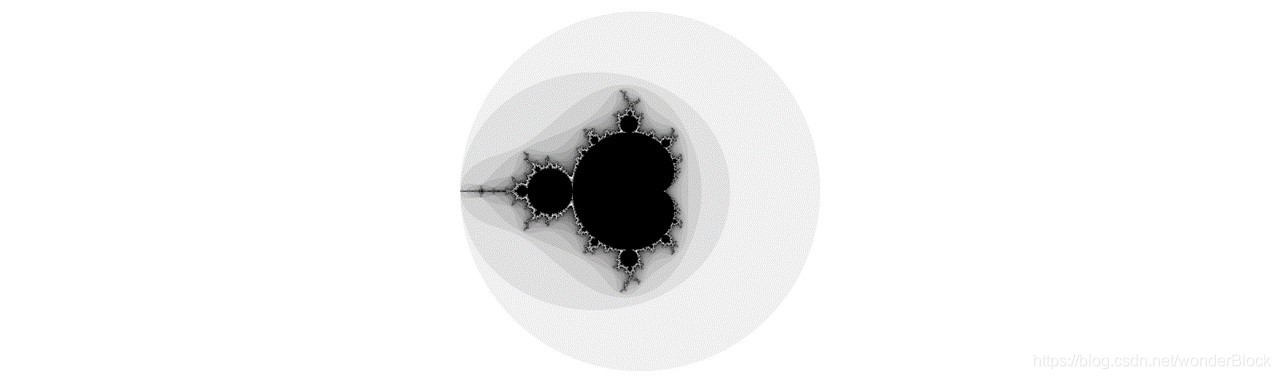
}程序中有两个循环在逐点读取一个1024 ＊ 1024的灰度珊格图像，该图像对应-2到+2之间的复数平面。程序会测试每个点，计算它们到圆心的距离是否超过2(这些点是否落在半径为2的原点)，如果超过了，这个点被它逃逸所用的循环次数所隐藏，如果没有，这个值归属于Mandelbrot集合并使用黑色标记。
最终程序将生成的文件 123.png：
扫一扫
1016
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
