数据结构之线性表

源代码：点击打开链接

1.引入

线性表的优点是可以在任意位置添加元素，删除元素，并且可以任意改变数据的长度。线性表的具体实现方法有顺序实现（数组），链式实现（链表）。而本文中线性表的实现是用链表实现（双向链表，用java实现）。对线性表的操作主要有增删改查。

2.原理

    要实现线性表，首先要有节点类Node<T>,其结构如下:

public class Node<T>
{
        private T data;//存储的数据
	private Node<T> pre;//上一个节点
	private Node<T> next;//下一个节点

}

    而Link类的数据结构如下：

public class Link<T> {
	private Node<T> head=new Node<T>() ;//头节点
	int count=0;//本链表中存储的元素个数
}

    下面是一个链表的结构示意图：

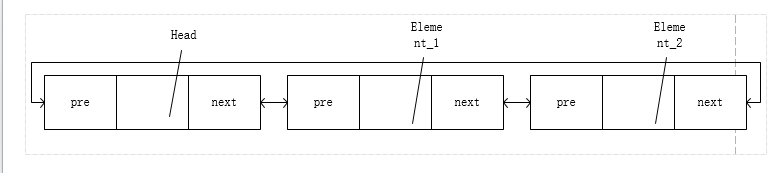
3.代码实现

    接下来将按增删改查的顺序实现。

    （1）增（add）：添加元素。有两种方式，一种是在链表队尾添加元素；另外一种是在指定位置添加元素。  

         /**
	 * 在链表队尾加入数据
	 * @param d
	 */
	public void add(T d)
	{
		if(count==0)
		{
			head.setData(d);
			++count;
			return ;
		}
		Node<T> n=new Node<T>(d);
		head.getPre().setNext(n);
		n.setPre(head.getPre());
		n.setNext(head);
		head.setPre(n);
		
		++count;
	}

    

        /**
	 * 在指定位置添加数据
	 * @param d
	 * @param index
	 */
	public void add(T d,int index)
	{
		
		Node<T> n=new Node<T>(d);
		//当插入位置不满足要求时返回
		if(index<0 || index>=count)
		{
			return ;
		}
		else
		{
			Node<T> temp=getNode(index);//这里的getNode(index)是获取本链表指定位置的节点
			Node<T> temp2=temp.getPre();
			temp2.setNext(n);
			temp.setPre(n);
			n.setPre(temp2);
			n.setNext(temp);
			if(index==0)//注意：当添加元素位置为0时，要将改变head指向的元素；
			{
				head=n;
			}
			++count;
		}
	}

    （2）删（remove）:删除指定位置的元素

        /**
	 * 删除制定位置的元素
	 * @param i
	 */
	public void remove(int i)
	{
		Node<T> temp=getNode(i);
		Node<T> temp1=temp.getPre();
		Node<T> temp2=temp.getNext();
		temp1.setNext(temp2);
		temp2.setPre(temp1);
		if(i==0)
		{
			head=temp2;
		}
		--count;
	}

    （3）改（replace）:替换指定位置的元素

        /**
	 * 改变index位置的元素
	 * @param index
	 * @param n
	 */
	public void replace(int index,T n)
	{
		Node<T> temp=getNode(index);
		temp.setData(n);
	}

    （4）查:获取指定位置的元素，查看本链表是否为空，本链表的大小。

        /**
	 * 获取指定index位置的元素
	 * @param index
	 * @return
	 */
	public T get(int index)
	{
		Node<T> temp=head;
		if(index<count/2)
		{
			//找到要插入的点
			
			for(int i=0;i<index;++i)
			{
				temp=temp.getNext();
			}
		}
		else
		{
			for(int i=count;i>index;--i)
			{
				temp=temp.getPre();
			}
		}
		return temp.getData();
	}
	
	/**
	 * 判读本链表是否为空
	 * @return
	 */
	public boolean isEmpty()
	{
		if(count==0)
		{
			return true;
		}
		else
		{
			return false;
		}
	}
	
	/**
	 * 获取本链表的大小
	 * @return
	 */
	public int getCount() {
		return count;
	}

4.实例解决--一元多项式的表示

4.1问题描述

    实现两个一元多项式的运算（相加，相减，相乘）。

    一元多项式在数学上可以表示为：

 

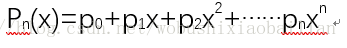
在计算机中，它可由一个线性表表示：

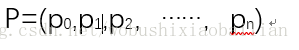
假设Qm(x)是一元m次多项式，设m<n,则两个多项式相加的结果Rn(x)=Pn(x)+Qm(x)可用线性表R表示：

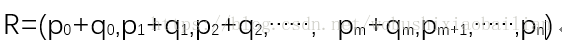
当然我们可以对P,Q,R用顺序存储的方式实现连个多项式的相加，但是在实际应用中，经常遇到多项式的次数很大且变化很大，使得顺序存储结构的最大长度很难确定。比如：

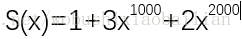
此时，就要用长度为2001的线性表来 表示，这对空间是极大的浪费。所以我们引入了下面一种对一元多项式的表示方法：

一般情况下的一元n次多项式可写成：

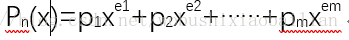；其中pi是指数为ei的项的非零系数，且满足0<=e1<=e2<=……<em=n;若用一个长度为m且每个元素有两个数据项（系数项和指数项）的线性表（(p1,e1),(p2,e2),……，（pm,em））便可唯一表示多项式Pn(x)。在最坏的情况下，n+1(=m)个系数都不为零，则比只存储每项系数的方案多存储一倍（因为多了e）的数据.

    

4.2设计思路

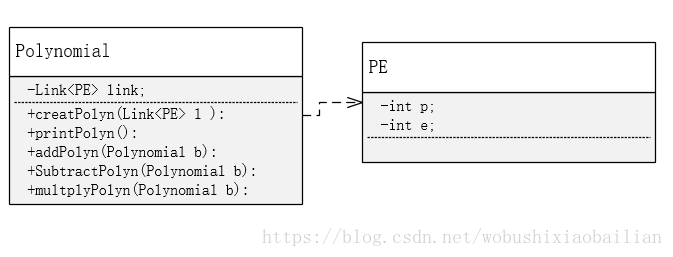
PE:是系数指数类，用于存储多项式每一项的系数和指数（分别为p,e）

creatPolyn():用链表l创建一个多项式对象

printPolyn():打印出本多项式

addPolyn():表示本多项式与多项式b相加

subtractPolyn():表示本多项式与多项式b相减

MultiplyPolyn():表示本多项式与多项式b相乘

4.3代码及运行结果

（1）实现两个多项式相加

流程图如下：

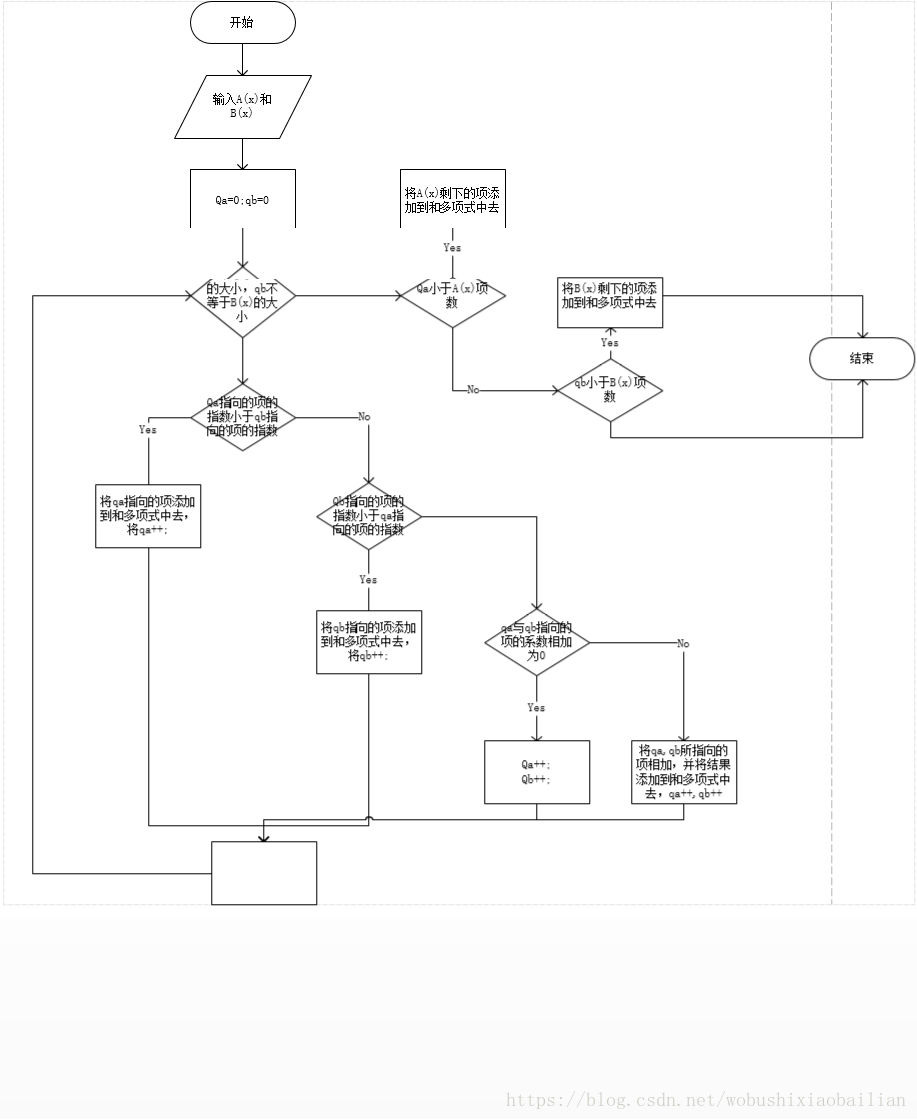
思路：假设指针qa和qb分别指向多项式A和多项式B中当前进行比较的某个节点，则比较两个节点中的指数项，有下面三种情况：

（1）指针qa所指向节点的指数值<指针qb所指向的指数值，则应摘取qa指针所指节点插入到“和多项式”中去，并让qa指针后移；

（2）指针qa所指向节点的指数值>指针qb所指向的指数值，则应摘取qb指针所指节点插入到“和多项式”中去，并让qb指针后移；

（3）指针qa所指向节点的指数值=指针qb所指向节点的指数值，则将两个节点中的系数相加。若和数不为0，则将相加的结果与指数值构造一个节点，然后添加到“和多项式”中去，再让qa，qb指针后移；若和数为0，则只让qa,qb指针后移就行了。

最后，将A(x)或B(x)剩余的项添加到和多项式中去。

    （2）实现两个多项式的相减。只要把B(x)的每一项取反就行了。

        /**
	 * 多项式的减法
	 * @param b
	 */
	public void SubtractPolyn(Polynomial b) {
		try {
			Polynomial temp=(Polynomial) b.deepClone();
		} catch (ClassNotFoundException | IOException e) {
			// TODO Auto-generated catch block
			e.printStackTrace();
		}
		for(int i=0;i<b.getL().getCount();++i)
		{
			b.getL().get(i).setP(-b.getL().get(i).getP());
		}
		addPolyn(b);
	}

    （3）实现多项式相乘。一元多项式的相乘，可以利用一元多项式的加法实现。因为乘法运算可以分解为多个加法运算。

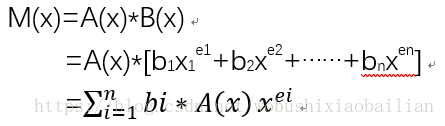
基本思路如下：

1. 首先，初始化一个和多项式sum
2. 将A(x)与B(x)的每一项相乘，得到一个新的多项式temp
3. 将2中得到的每一个temp与sum相加。

代码如下：

        public void multplyPolyn(Polynomial b) throws OptionalDataException, ClassNotFoundException, IOException {
		Polynomial sum=new Polynomial();
		for(int i=0;i<b.getL().getCount();++i)
		{
			Polynomial temp=(Polynomial) this.deepClone();
			for(int j=0;j<temp.getL().getCount();++j)
			{
				temp.getL().get(j).setP(l.get(j).getP()*b.getL().get(i).getP());
				temp.getL().get(j).setE(l.get(j).getE()+b.getL().get(i).getE());
			}
			sum.addPolyn(temp);
		}
		l=sum.getL();
	}

源代码将文章最前面！！！！！请高抬贵手，点击一下左上角的小手。