改进的鼠群优化算法，原理详解，MATLAB代码免费获取

Rat Swarm Optimizer（RSO）算法是近年来发展起来的一种启发式算法，它的灵感来自于老鼠的自然行为，特别是它们的追逐和攻击策略。RSO在解决优化问题方面已被证明是有效的;然而，RSO面临着一些限制，阻碍了其在复杂优化任务中的性能。为了解决这些缺点，改进的鼠群优化算法（MRSO）被提出，旨在增强探索和开发之间的平衡。MRSO结合了独特的修改，以提高搜索效率和鲁棒性，使其适合具有挑战性的工程问题。

该成果于2024年发表在计算机领域四区SCI期刊“Algorithms”上。当应用于工程设计问题时，MRSO始终提供比RSO更好的平均结果，证明了其有效性。

1、算法原理

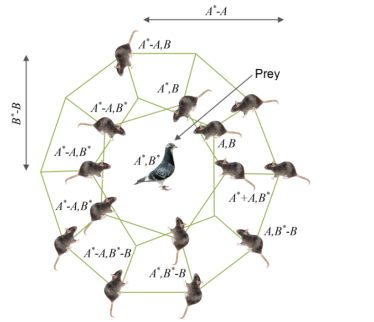
（1）追逐猎物

老鼠的追逐行为是一种典型的社会活动。最有效的搜索代理被确定为知道猎物位置的老鼠。其余的人根据这只最好的老鼠的位置调整他们的位置，如下所述：

其中， 表示第i个rat（解）的位置，（t）表示当前迭代次数。 表示到目前为止找到的最佳候选解的位置。（A）的计算如下：

R和C是随机值，其中R的范围在[1，5]之间，并且C的范围在[0，2]之间。这些值用作算法中探索和利用机制的参数：

（2）与猎物战斗

战斗行为在数学上用以下方式表示：

大鼠编号i的下一个位置表示为 。参数A和C对于平衡勘探和开采机制至关重要。小的A值（例如，1)与中等的C值相结合，强调开发，而其他值可能会将重点转向探索。

（3）改进的鼠群优化算法（MRSO）

改进的鼠群优化算法（MRSO）旨在通过平衡探索和利用来提高RSO的性能。这种平衡是通过“追逐猎物”部分中的函数实现的，它是静态的，依赖于单个参数C。在MRSO中，该功能重新表述如下：

公式更新如下：

在初始化参数A Modified、C和R之后，使用目标函数评估结果，其中最佳解保存为 。然后使用等式更新大鼠的位置，并且更新参数R、A和A Modified。如果一只老鼠的位置超出了搜索空间，它会被重新分配到先前的中心进行调整。然后通过目标函数来测试和评估每只大鼠的位置。如果找到比 更好的解，则将 更新到该新的最佳位置。此过程将通过最大迭代次数（Maxiteration）继续。最终，使用识别的最佳位置 来选择位置。这些修改通过获得最佳适应度函数来提高性能。

下图显示了MRSO的流程图和伪代码。

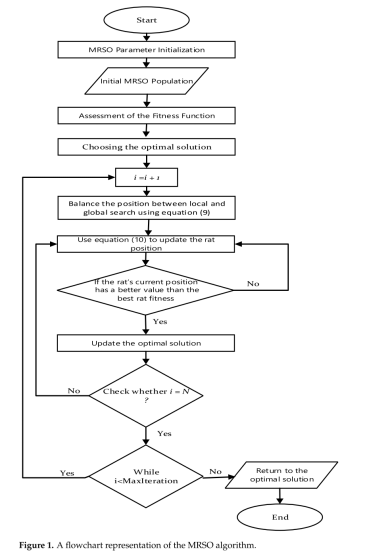
MRSO对应的伪代码过程如下图所示

2、结果展示

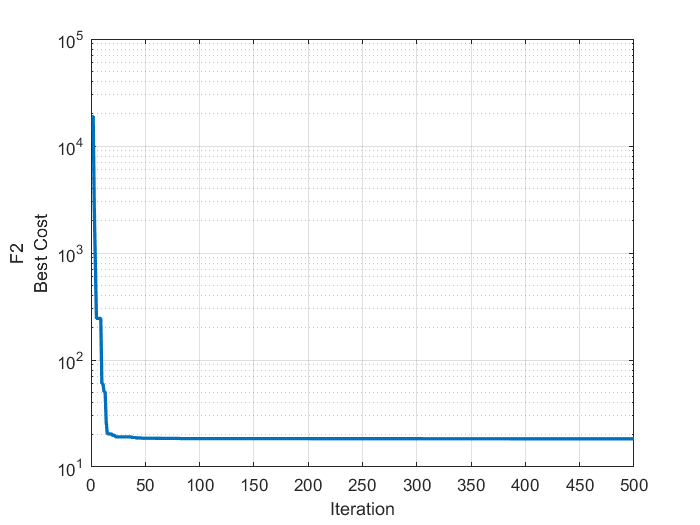
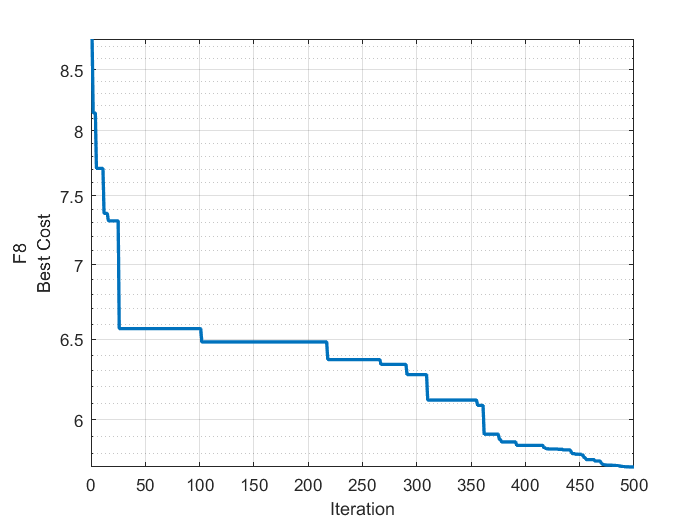
3、MATLAB核心代码

% 改进的鼠群优化算法（Modified Rat Swarm Optimization，MRSO)
function [output] = MRSO(itt,F)
        for n=1:itt
            Function_name=F;                         % Name of the test function from beanchmark test functions
            [lb,ub,dim,fobj]=CEC2019(Function_name);
            ShowIterInfo = true;                     % Flag for Showing Iteration Information                              
            MaxIt = 500;                             % max Iteration numbers
            nPop = 30;                               % Population size
            
            Position=zeros(1,dim);
            Score=inf; 
            Positions=init(nPop,dim,ub,lb);          %initialization
            Convergence=zeros(1,MaxIt);
            l=0;                                      %% Parameters of MRSO
            x = 1;
            y = 5;
            R = floor((y-x).*rand(1,1) + x);            % equation No. (3)
            for it=1:MaxIt
%                         
                    for i=1:size(Positions,1)  
                    Flag4Upper_bound=Positions(i,:)>ub;
                    Flag4Lower_bound=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4Upper_bound+Flag4Lower_bound)))+ub.*Flag4Upper_bound+lb.*Flag4Lower_bound;               
                    fitness=fobj(Positions(i,:));
                    if fitness<Score 
                        Score=fitness; 
                        Position=Positions(i,:);
                    end
                    end
                     F1=R-l*((R)/MaxIt);               % equation No. (6)
                     F2=(1-it*((1)/MaxIt));            % equation No. (7)
                     F3=(2*rand-1*rand);               % equation No. (8)  
                     Ar=F1*F2*F3;                      % equation No. (9)              
                for i=1:nPop
                    for j=1:dim     
                        C=2*rand();                     % equation No. (4)           
                        Positions(i,j)=Position(j)-(Ar*Positions(i,j)+abs(C*((Position(j)-Positions(i,j))))); % equation No. (1)
                    end
                end
                l=l+1;    
                Convergence(it)=Score;
                % Display Iteration Information
                if ShowIterInfo
                    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(Convergence(it))]);
                end
            end
            out.pop = Positions;
            out.BestSol = Score;
            out.BestCosts = Convergence;
            semilogy(Convergence, 'LineWidth', 2);
            xlabel('Iteration');
            ylabel('Best Cost');
            grid on;
            output = zeros(itt, 1);
            output1 (n) = Score; % added!
            output = output1;
        end
end

参考文献

[1]Abdulla H S, Ameen A A, Saeed S I, et al. MRSO: Balancing Exploration and Exploitation through Modified Rat Swarm Optimization for Global Optimization[J]. Algorithms, 2024, 17(9): 423.

完整代码获取

下方卡片获取