中科院一区论文复现，改进蜣螂算法，Fuch映射+反向学习+自适应步长+随机差分变异，Python代码...

最新推荐文章于 2025-03-31 09:49:37 发布

转载最新推荐文章于 2025-03-31 09:49:37 发布 · 443 阅读

CC 4.0 BY-SA版权

原文链接：https://mp.weixin.qq.com/s?__biz=MzkyNDUwMjc3Mg==&mid=2247487373&idx=1&sn=e62f8b12edd4b0b2f92fa6cc6155c969&chksm=c0187e99f177663f5468f3b7e0a0549d8e87b3082a0a98e8f49d1ea1525901cb6b6f4f5d5140&scene=126&sessionid=0

文章标签：

#算法 #学习 #python #开发语言

本文介绍了如何将MATLAB中的蜣螂算法转换为Python，重点讨论了融合混沌和逆向学习策略、自适应步长与凸透镜成像策略以及随机差异变异策略的改进。通过在多个CEC函数集上的实验，展示了改进算法的性能提升。

有小伙伴后台不断留言，要求将蜣螂算法的MATLAB语言变更为Python语言。话不多说，安排！

本期文章采用Python代码复现一篇发表于2024年来自中科院一区TOP顶刊《Energy》的改进蜣螂算法

论文引用如下：

Li Y, Sun K, Yao Q, et al. A dual-optimization wind speed forecasting model based on deep learning and improved dung beetle optimization algorithm[J]. Energy, 2024, 286: 129604.

改进的蜣螂优化算法原理如下：

改进策略

改进点1： 融合Fuch混沌与逆向学习策略在种群初始化的应用

种群初始化在DBO中随机生成，会导致种群初始化分布不均匀，导致初始化种群的多样性。融合混沌和逆向学习策略进行群体初始化，将混沌初始化方法和逆向学习初始化策略相结合，以提高DBO的收敛速度。

Fuch混沌映射公式如下：

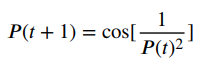
在使用Fuch混沌映射生成初始解的同时，引入反向学习策略。扩大了蜣螂的搜索空间，以提高种群初始解决方案的质量。反向学习策略的数学表达式如下式所示：

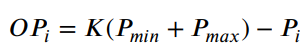
其中 OPi 是对应于每个初始解 Pi 的逆解。Pmax 和 Pmin 分别表示初始解中的最大值和最小值。K 是（0， 1）范围内的随机值。

改进点2： 自适应步长策略与凸透镜成像策略的集成

由于DBO采用随机策略，在蜣螂觅食阶段缺乏自适应能力，全局搜索能力较弱，容易陷入局部最优。为了进一步提高算法的寻道性能，该文采用动态选择策略，在一定概率下交替使用自适应步长策略和凸透镜成像反转策略来更新目标位置。

在初期迭代中，大步长能够扩展觅食搜索，提高算法的全局搜索能力，促进算法更快地找到更优的解，加快收敛速度。在后期迭代中，小步长有利于算法的局部搜索。步长的规律变化在觅食蜣螂的搜索中起着指导作用，这意味着在整体环境中从全局搜索逐渐过渡到局部搜索。该策略主要由线性递减的自适应步进控制因子α0决定，如下所示：

同时，引入一种凸透镜成像学习策略来扰动蜣螂种群，以增强种群多样性，提高算法跳出局部最优的可能性。该等式表示如下：

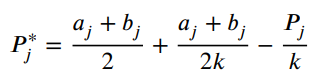
该策略在之前提出的改进算法中也有详细介绍，具体请看：三种策略改进的沙猫群优化算法(MSCSO)

目标位置更新采用哪种策略的选择由选择概率 Ps 决定，

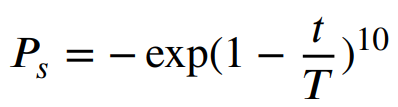
当随机值Ps<0.5时，采用随机步进策略对蜣螂进行位置更新;否则，凸透镜反向学习策略用于位置更新，如下方程所示：

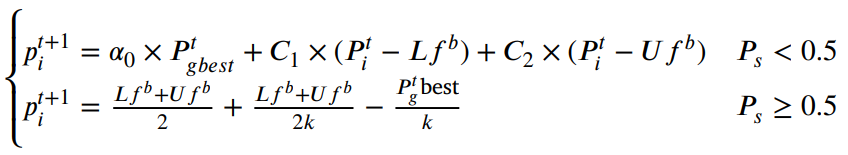
改进点3： 随机差异变异策略

蜣螂偷窃行为的位置更新方程根据个体的当前最优值更新其位置，这可能导致种群多样性的减少。导致算法陷入局部最优状态，收敛精度效率低下。因此，本文引入随机差分变异策略来增强偷蜣螂种群多样性。公式如下：

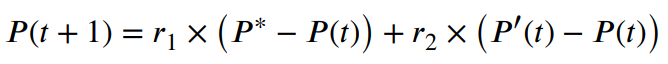
其中 P (t+1)表示通过随机差异突变获得的新个体，r1 和 r2 是 [0,1] 范围内的随机值。P∗ 是当前最佳个人位置。P′(t)是从种群中随机选择的个体的位置。

结果展示

利用python强大的opfunu库，集成了CEC2005/2008/2010/2013等11个CEC函数库。

pip install opfunu  # 参考文档：https://github.com/thieu1995/opfunu

本期文章将改进的蜣螂算法与原始算法在多个CEC函数集上进行对比。并画出函数图像，迭代曲线。

在CEC2005中测试：

F1:

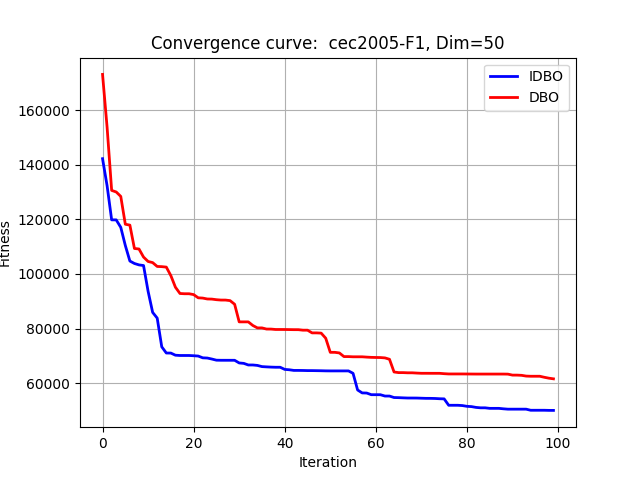
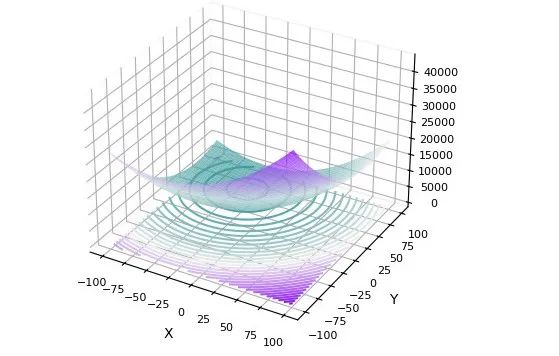
F2:

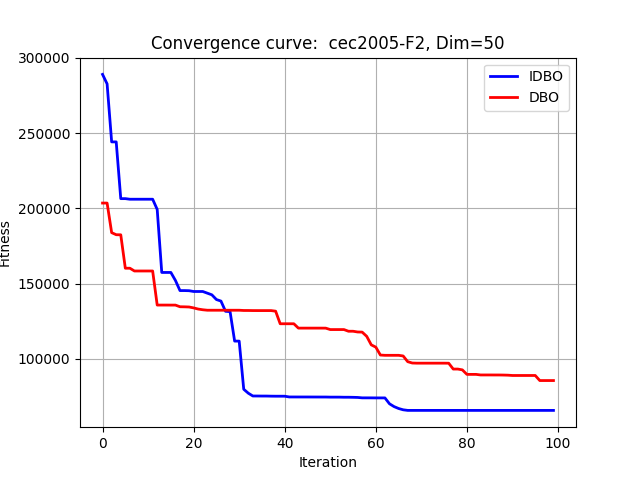
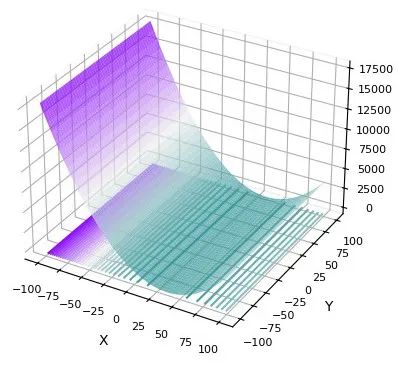
在CEC2008中测试：

F1:

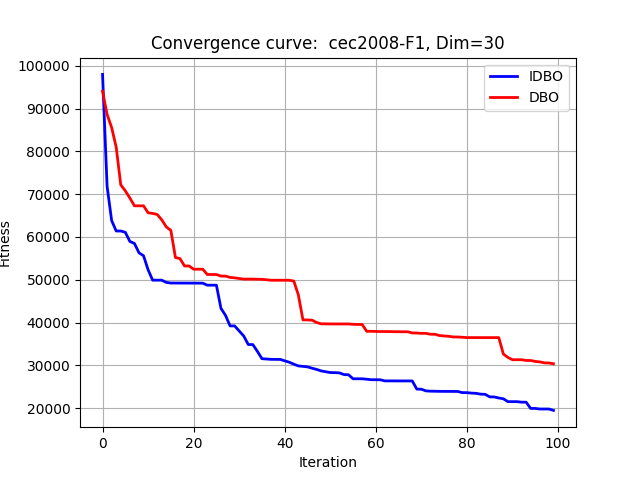
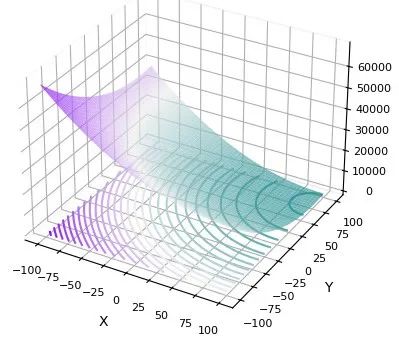
在CEC2010中测试：

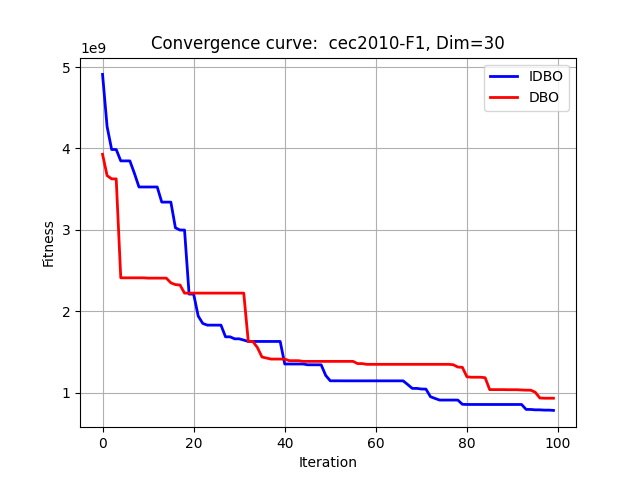
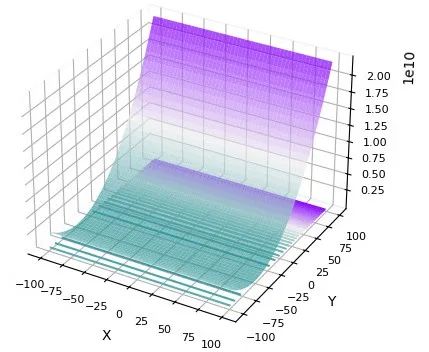
在CEC2021中测试：

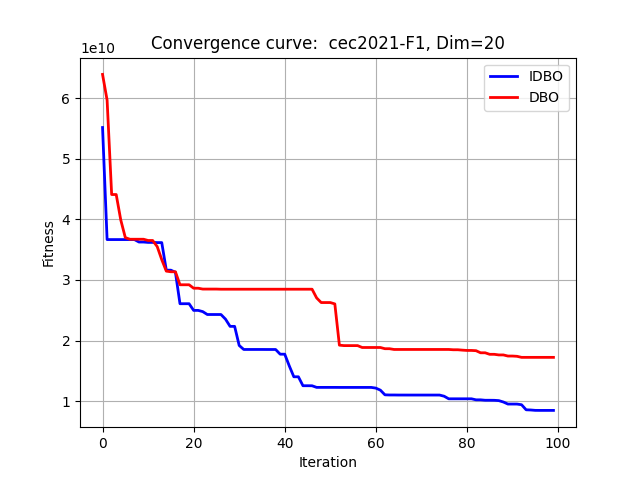
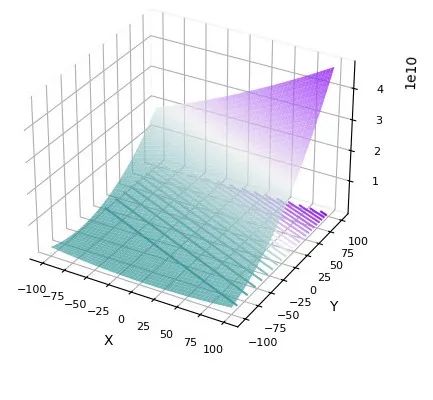
在CEC2022中测试：

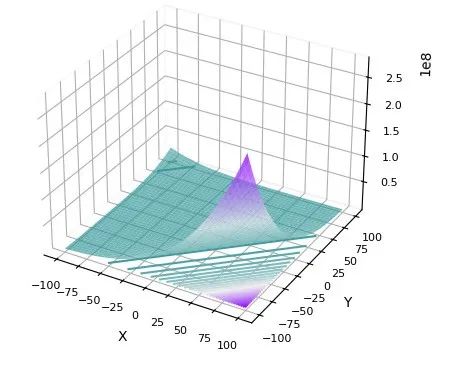
其他函数集就不再一一展示。注意：改进的算法并非对任何函数效果都最佳，所有的改进算法只能保证对大部分函数有较好效果。

需要的包版本如下：

matplotlib~=3.8.2
numpy~=1.26.3
opfunu~=1.0.1

部分代码展示

import numpy as np
from matplotlib import pyplot as plt
# In[]:
import opfunu # 参考：https://github.com/thieu1995/opfunu
import copy  # 导入copy模块，用于对象的复制。
import math
'''
适应度函数及维度dim的选择
cec函数名字格式：函数名+年份，比如要选择2022的F1函数，func_num = 'F1'+'2022'
cec2005：F1-F25, 可选 dim = 10, 30, 50
cec2008：F1-F7,  可选 2 <= dim <= 1000
cec2010：F1-F20, 可选 100 <= dim <= 1000
cec2013：F1-F28, 可选 dim = 2, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
cec2014：F1-F30, 可选 dim = 10, 20, 30, 50, 100
cec2015：F1-F15, 可选 dim = 10, 30
cec2017：F1-F29, 可选 dim = 2, 10, 20, 30, 50, 100
cec2019：F1-F10, 可选 dim: F1=9,F2=16,F3=18,其他=10
cec2020：F1-F10, 可选 dim = 2, 5, 10, 15, 20, 30, 50, 100
cec2021：F1-F10, 可选 dim = 2, 10, 20
cec2022：F1-F12, 可选 dim = 2, 10, 20


'''


'''边界检查函数'''
def boundary(pop, lb, ub):
    # 定义一个边界检查函数，确保种群中的个体不超出预定义的边界。
    pop = pop.flatten()
    lb = lb.flatten()
    ub = ub.flatten()
    # 将输入参数扁平化，以便进行元素级操作。


    # 防止跳出范围,除学习率之外 其他的都是整数
    pop = [int(pop[i]) if i > 0 else pop[i] for i in range(lb.shape[0])]
    # 将除了学习率以外的参数转换为整数。


    for i in range(len(lb)):
        if pop[i] > ub[i] or pop[i] < lb[i]:
            # 检查个体是否超出边界。
            if i == 0:
                pop[i] = (ub[i] - lb[i]) * np.random.rand() + lb[i]
                # 如果是学习率，则在边界内随机选择一个值。
            else:
                pop[i] = np.random.randint(lb[i], ub[i])
                # 对于整数参数，随机选择一个边界内的整数值。


    return pop
    # 返回修正后的个体。


''' 种群初始化函数 '''
def initial(pop, dim, ub, lb):
    # 定义一个初始化种群的函数。
    X = np.zeros([pop, dim])
    # 创建一个形状为[种群大小, 维度]的零矩阵。


    for i in range(pop):
        for j in range(dim):
            X[i, j] = np.random.rand() * (ub[j] - lb[j]) + lb[j]
            # 在边界内随机初始化每个个体的每个参数。


    return X, lb, ub
    # 返回初始化后的种群及边界。


'''计算适应度函数'''
def CaculateFitness(X):
    # 定义一个计算适应度的函数。
    pop = X.shape[0]
    # 获取种群的大小。
    fitness = np.zeros([pop, 1])
    # 创建一个形状为[种群大小, 1]的零矩阵来存储适应度。


    for i in range(pop):
        fitness[i] = cec_fun(X[i, :])
        # 对每个个体调用适应度函数进行计算。


    return fitness
    # 返回计算得到的适应度。


'''适应度排序'''
def SortFitness(Fit):
    # 定义一个对适应度进行排序的函数。
    fitness = np.sort(Fit, axis=0)
    # 按适应度大小进行排序。
    index = np.argsort(Fit, axis=0)
    # 获取排序后的索引。


    return fitness, index
    # 返回排序后的适应度和索引。


'''根据适应度对位置进行排序'''
def SortPosition(X, index):
    # 定义一个根据适应度排序位置的函数。
    Xnew = np.zeros(X.shape)
    # 创建一个与X形状相同的零矩阵。


    for i in range(X.shape[0]):
        Xnew[i, :] = X[index[i], :]
        # 根据适应度的排序结果重新排列位置。


    return Xnew
    # 返回排序后的位置。

本期代码获取

https://mbd.pub/o/bread/ZZuWkpts

扫面二维码亦可跳转：