_10-红黑树的插入

题意：

本道题测试通过不同的用例帮助你完成红黑树的插入，有几点需要注意：

1. 节点的颜色以枚举RBTREECOLOR来表示，共有RED，BLACK和ROOT三种颜色，ROOT是为了方便编码特地规定的虚拟根节点的颜色。请注意看模板代码。
2. 依习惯，整个树挂在虚拟根节点-1的右节点上。-1节点的颜色为ROOT，可以方便判断根节点。
3. 以红黑树定义来说，如果节点的左右子树为空，应当视为挂载了黑色节点，《算法导论》中采用一个特别的NIL节点来替代NULL，本题不采用这一解法，还是为空指针，请注意处理空结点的颜色问题。
4. 节点包含parent指针，请注意维护。

请你填写插入函数，

void insert_rb_node( BTreeNode* root, int value );

 思路：

大体分为节点的插入与修复。

先再复述一下红黑树的性质：

        一、每个节点非红即黑。

        二、根节点是黑色。

        三、每个叶节点是黑色。

        四、红节点的叶子节点必为黑。

        五、对每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

①插入。其过程与二叉搜索树相。需要注意两点：一是将插入的节点设置为RED，二是一定在叶子节点插入。

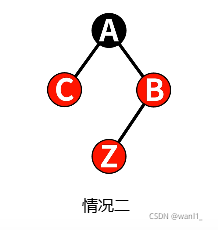
②修复。因为插入的节点我们设置为红色，若父节点为黑色，我们则不需要修复，即只需考虑父节点为红色的情况。我们分为下列四种情况：（将插入的节点设置为z、与z同一个父节点的兄弟节点称叔节点）

        一、z是根节点。

        二、z的叔节点是红色。

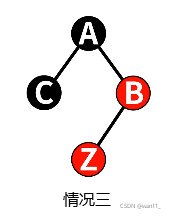
        三、z的叔节点是黑色，且z局部呈现三角形。

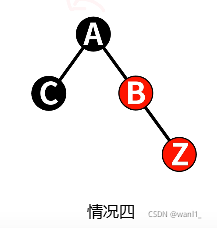
        四、z的叔节点是黑色，且z局部呈现直线。

        对于情况一，我们只需将其由红色改为黑色即可。

        对于情况二，我们选择将其父节点和叔节点颜色变为黑色，其祖父节点变为红色，并将z替换为z的祖父节点，再放到循环里去解决。

        对于情况三，我们选择将z的父节点进行右旋（左旋），并将z替换为z的父节点。这样做把情况三归结为情况四。

        对于情况四，我们选择将z的父节点变为黑色，z的祖父节点变为红色，并对z的祖父节点进行左旋（右旋）。

        ps：进行左旋还是右旋需要判断z的父节点属于z的祖父节点的左节点还是右节点，详情看后续代码。

 

③旋转。由于红黑树的树结构没有高度，所以它旋转时不用考虑高度，其余与二叉搜索树左右旋操作相似。

源码：

//
//enum RBTREECOLOR{
//    RED,
//    BLACK,
//    ROOT, // 专门定义一个root颜色方便处理
//};
//
//struct BTreeNode{
//    int value{0};
//    RBTREECOLOR color{RED};
//    BTreeNode* parent{nullptr};
//    BTreeNode* left_child{nullptr};
//    BTreeNode* right_child{nullptr};
//    BTreeNode( int value ){
//        this->value = value;
//    }
//    BTreeNode( int value, RBTREECOLOR color ){
//        this->value = value;
//        this->color = color;
//    }
//    BTreeNode(){
//        this->value = 0;
//    }
//};
void rotate_ll(BTreeNode* node) {
	if (!node) return;
	BTreeNode* t = node->left_child;
	node->left_child = t->right_child;
	if (t->right_child)
		t->right_child->parent = node;
	t->parent = node->parent;
	if (node->parent->right_child == node)
		node->parent->right_child = t;
	else
		node->parent->left_child = t;
	t->right_child = node;
	node->parent = t;
}
void rotate_rr(BTreeNode* node) {
	if (!node)return;
	BTreeNode* t = node->right_child;
	node->right_child = t->left_child;
	if (t->left_child)
		t->left_child->parent = node;
	t->parent = node->parent;
	if (node->parent->right_child == node)
		node->parent->right_child = t;
	else
		node->parent->left_child = t;
	t->left_child = node;
	node->parent = t;
}
void rotate_rl(BTreeNode* node) {
	BTreeNode* t = node->right_child;
	rotate_ll(t);
	rotate_rr(node);
}
void rotate_lr(BTreeNode* node) {
	BTreeNode* t = node->left_child;
	rotate_rr(t);
	rotate_ll(node);
}
void rb_insert_fixup(BTreeNode* z) {
	/*
	修复颜色，因为插入的点，我们总是将其先染成红色，
	所以如果父节点为黑色则不需要修复，如果父节点为红色，则需要修复。
	有四种情况：
		一、z是根节点
		二、z的叔节点y是红色
		三、z的叔节点y是黑色，且z是一个右孩子
		四、z的叔节点y是黑色，且z是一个左孩子
	*/
	if (z->parent == nullptr) {  //情况一
		z->color = BLACK;
		return;
	}
	while (z->parent->color == RED) {
		if (z->parent == z->parent->parent->left_child) {  //如果z的父节点是祖父节点的左节点
			BTreeNode* y = z->parent->parent->right_child;  //定义y为z的叔节点
			if (y&&y->color == RED) {  //情况二
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;
				z = z->parent->parent;
			}
			else if (z == z->parent->right_child) {  //情况三
				z = z->parent;
				rotate_rr(z);
			}
			else {  //情况四
				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rotate_ll(z->parent->parent);
			}
		}
		else {  //如果z的父节点是祖父节点的右节点
			BTreeNode* y = z->parent->parent->left_child;
			if (y&&y->color == RED) {  //情况二
				z->parent->color = BLACK;
				z->parent->parent->left_child->color = BLACK;
				z->parent->parent->color = RED;
				z = z->parent->parent;
			}
			else if (z->parent == z->parent->parent->left_child) {  //情况三
				z = z->parent;
				rotate_ll(z);
			}
			else {  //情况四
				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rotate_rr(z->parent->parent);
			}
		}
	}
	while (z->parent->value != -1)
		z = z->parent;
	z->color = BLACK;
}
void insert_rb_node( BTreeNode* root, int value ){
BTreeNode* n = new BTreeNode(value);  //定义待插入节点n
	BTreeNode* y = nullptr;
	while (root) {  //二叉搜索寻找插入的位置
		y = root;
		if (root->value > value)
			root = root->left_child;
		else
			root = root->right_child;
	}
	n->parent = y;  //找到合适的插入位置，设置新节点的父节点
	if (!y)  //如果是空树
		root = n;
	else if (y->value > n->value)  //在y的左节点
		y->left_child = n;
	else                           //在y的右节点
		y->right_child = n;
	n->left_child = n->right_child = nullptr;
	rb_insert_fixup(n);
}