目录
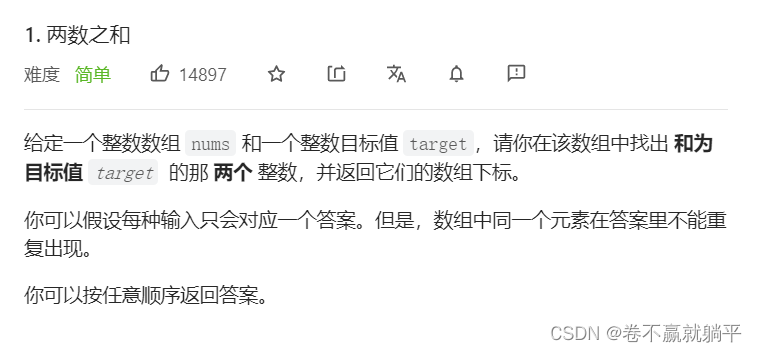
题目描述

 解法一
解法一
暴力解法,双重循环依次遍历,返回两数之和等于target的下标。时间复杂度O(N^2),空间复杂度O(1)。代码如下:
public static int[] TwoSum(int[] nums,int target){
if(nums == null || nums.length < 2) {
return new int[] {};
}
for(int i = 0;i < nums.length - 1; i++) {
for(int j = i + 1;j < nums.length; j++) {
if(nums[i] + nums[j] == target) {
return new int[] {i,j};
}
}
}
return new int[] {};
}解法二
二分法,由于二分查找需要对有序的数组进行操作,但是对原始数组进行排序之后会破坏原数组对应的下标,所以我们还需要一个map来存储原数组元素对应的下标,这样一来对应的时间复杂度(排序+查找)为O(NlogN),空间复杂度因为有额外的map,所以为O(N)。相比而言有些过于麻烦,所以本道题目不选择这种解法。
解法三
哈希查找。我们可以先new一个hashmap,然后将数组对应的元素和下标存储在哈希map中,然后只需要遍历一遍哈希表就可以找到两数之和为target的下标了。时间复杂度为O(N),空间复杂度也为O(N)。代码如下:
public static int[] TwoSum(int[] nums,int target) {
if(nums == null || nums.length < 2) {
return new int[] {};
}
HashMap<Integer,Integer> map = new HashMap<>();
for(int i = 0;i < nums.length;i++) {
map.put(nums[i], i);
}
for(int i = 0;i < nums.length;i++) {
int x = nums[i];
if(map.containsKey(target - x)) {
int index = map.get(target - x);
if(i != index) {
return new int[] {i,index};
}
}
}
return new int[] {};
}解法三代码优化:
public static int[] TwoSum(int[] nums,int target) {
if(nums == null || nums.length < 2) {
return new int[] {};
}
HashMap<Integer,Integer> map = new HashMap<>();
for(int i = 0;i < nums.length;i++) {
int x = nums[i];
if(map.containsKey(target - x))
{
int index = map.get(target - x);
return new int[] {i,index};
}
map.put(x, i);
}
return new int[] {};
}20220723





 这篇博客探讨了三种解决两数之和问题的方法:暴力解法、二分查找和哈希查找。其中,哈希查找法在时间复杂度为O(N)的情况下找到了最优解决方案,避免了重复遍历,提高了效率。代码示例展示了如何利用哈希表在不改变原始数组顺序的情况下找到目标和的两个数的下标。
这篇博客探讨了三种解决两数之和问题的方法:暴力解法、二分查找和哈希查找。其中,哈希查找法在时间复杂度为O(N)的情况下找到了最优解决方案,避免了重复遍历,提高了效率。代码示例展示了如何利用哈希表在不改变原始数组顺序的情况下找到目标和的两个数的下标。
















 715
715

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








