Harris角点检测

最新推荐文章于 2025-03-05 22:01:12 发布

雨点ing

最新推荐文章于 2025-03-05 22:01:12 发布

阅读量510

点赞数

分类专栏： OpenCV

本文链接：https://blog.youkuaiyun.com/winggyn/article/details/113118889

版权

OpenCV 专栏收录该内容

32 篇文章

订阅专栏

Harris实现过程：

计算图像在X和Y方向的梯度：

$I_{x}=\partial I/\partial x=I\bigotimes \begin{pmatrix} -1 & 0 & 1 \end{pmatrix}; I_{y}=\partial I/\partial y=I\bigotimes\begin{pmatrix} -1 & 0 & 1 \end{pmatrix}^{T}$

计算图像两个方向梯度的乘积

$I_{x}^{2}=I_{x}\cdot I_{x},I_{y}^{2}=I_{y}\cdot I_{y},I_{xy}^{2}=I_{x}\cdot I_{y}$

使用高斯函数对三者进行高斯加权，生成矩阵M的A，B，C；

$A=g(I_{x}^{2})=I_{x}^{2}\bigotimes \omega ; C=g(I_{y}^{2})=I_{y}^{2}\bigotimes \omega ; B=g(I_{xy})=I_{xy}\bigotimes \omega ;$

计算每个像素的Harris相应值R，并对小于某一阈值t的R置为零；

在3*3或者5*5邻域内进行非最大值抑制，局部最大值点即为图像中的角点。

cv2.cornerHarris()参数如下：

img-数据类型为float32的输入图像

blocksize-角点检测中的领域大小

ksize-Sobel求导中使用的窗口大小

k-Harris角点检测方程中的自由参数，取值参数为[0.04,0.06]

import cv2
import numpy as np

img = cv2.imread('test5.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)
#输入图像必须是float32,最后的一个参数在0.04到0.06之间
dst = cv2.cornerHarris(gray,2,3,0.03)
#结果进行膨胀，可有可无
dst = cv2.dilate(dst,None)
print(dst)
#设定阈值，不同图像阈值不同
img[dst>0.01*dst.max()]=[0,0,255]
print(dst.max())
cv2.imshow('dst_img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

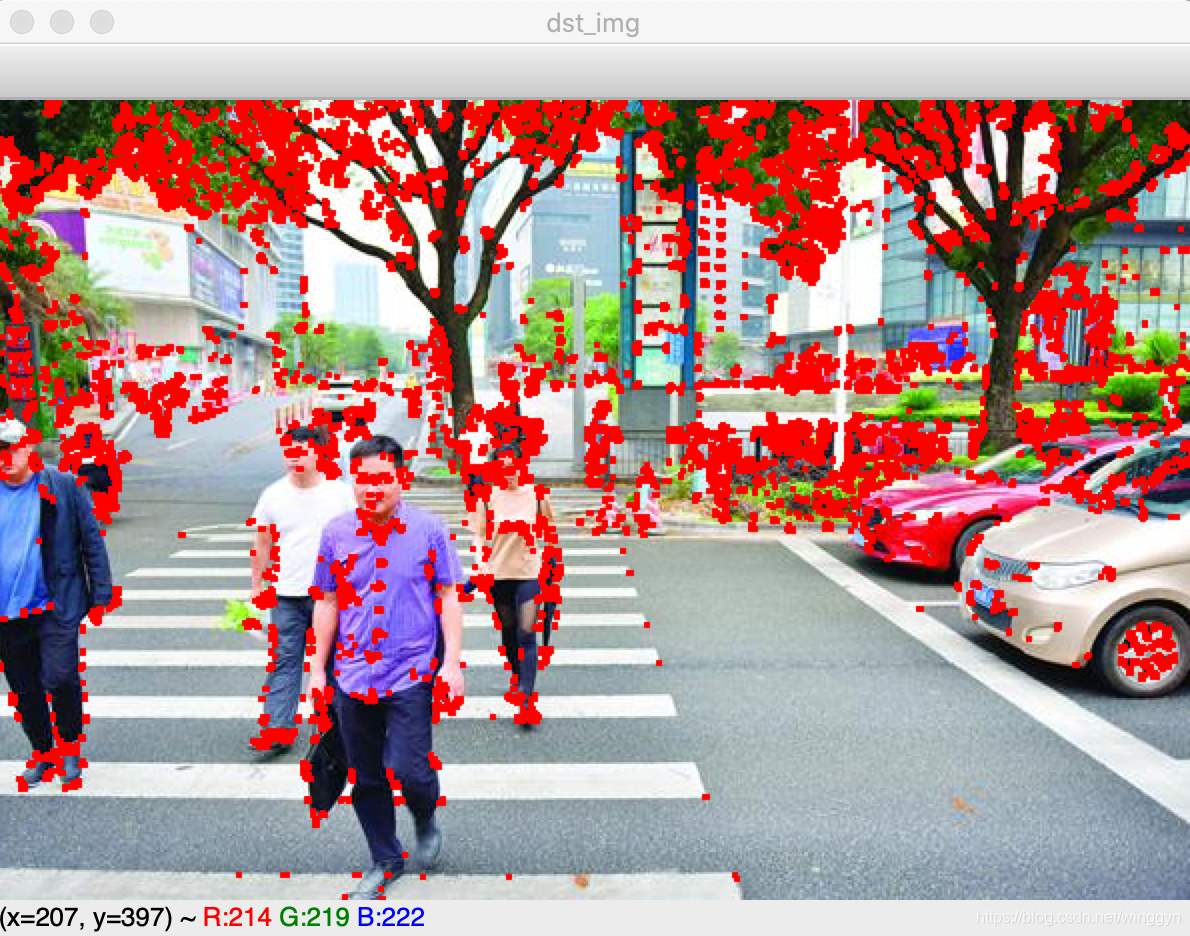
参数为0.03和0.06时候的结果比较。。。。

SIFT代码：

import cv2
import numpy as np
img = cv2.imread('test.jpg')
gray =cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
sift = cv2.xfeatures2d.SIFT_create()
kp = sift.detecgt(gray,None)
img = cv2.drawKeyPoints(gray,kp,img)
cv2.imshow('sp',img)
cv2.waitKey()
#需要最新的才可以执行