贝塞尔曲线实现原理

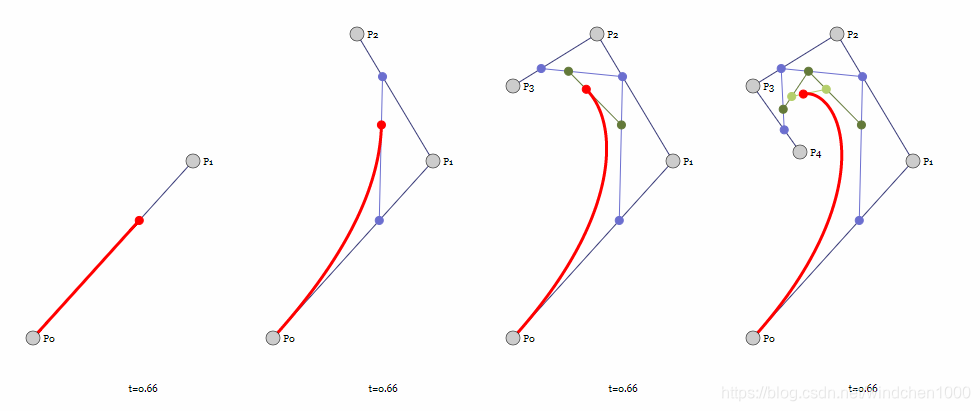
如图，一阶（两点）贝塞尔、二阶（三点）贝塞尔、三阶（四点）贝塞尔、四阶（五点）贝塞尔
Bezier原理其实不复杂~

一阶贝塞尔（直线）

一阶贝塞尔由两个点确定：$P0$和$P1$，$P0$是起点，$P1$是终点
当时间$t$在0~1区间变化时，根据该曲线公式，可以得到多个点坐标，这些点坐标，实际就形成一条直线
$$P(t)=P0+(P1-P0)\ast t$$
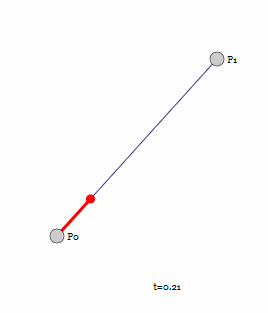
如下图：

二阶贝塞尔（曲线）

二阶贝塞尔由3个点确定：$P0$、$P1$、$P2$，$P0$是起点，$P2$是终点，$P1$是控制点
他实际上可以分解为两个一阶贝塞尔，$P0$-$P1$和$P1$-$P2$
根据一阶贝塞尔曲线，我们知道可以根据两个点算出一个新的中间点坐标，因此，$P0$-$P1$=>$Pm$，$P1$-$P2$=>$Pn$
这样，三个点$P0$ $P1$ $P2$，就转换成了两个点$Pm$ $Pn$
接着，再套用一阶贝塞尔，将$Pm$-$Pn$=>$P(t)$，生成的点，就构成了一个曲线
$$Pm=P0+(P1-P0)\ast t$$
$$Pn=P1+(P2-P1)\ast t$$
$$P(t)=Pm+(Pn-Pm)\ast t$$
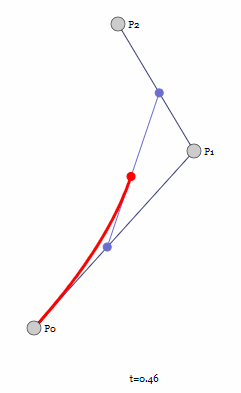
生成曲线如下：

多阶贝塞尔

更多阶贝塞尔，其实就是分解成多个二阶贝塞尔，生成新的点，再构成二阶贝塞尔，多次重复叠加计算，就可以生成曲线了

参考

• 贝塞尔曲线原理示意图：
  https://www.jasondavies.com/animated-bezier/