CS231n学习笔记——SGD、AdaGrad、RMSProp、Adam

CS231n学习笔记——更好的优化算法

SGD的缺点：
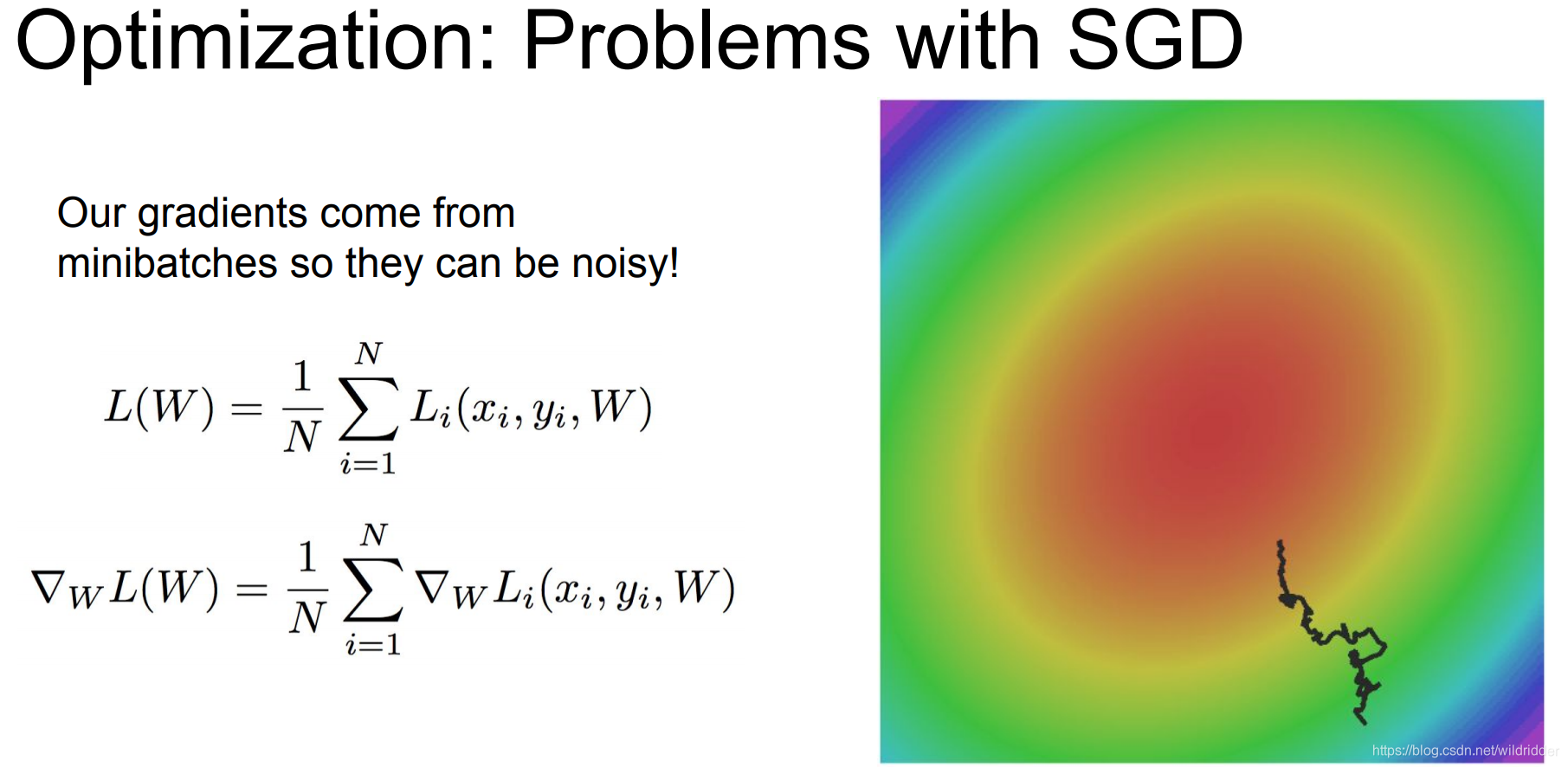
优化的轨迹会如图所示，因为很多函数的梯度方向并不是直接朝向最小值的，所以沿着梯度前进的时候可能会来回反复。这个问题在高维空间中更加普遍，

而且SGD很容易陷入局部最小值
而且在mini batch训练中，每次都取出一小部分数据学习梯度，导致学习到的梯度与正真的梯度有些偏差，特别是在存在噪声的数据中，这样的SGD可能需要更多时间去找到最小值点

而在随机梯度下降中加入一个动量项，

构造一个保持不变的项——速度v，把每一次算出来的梯度都加到这个速度上，在这个速度方向上步进而不是梯度上。这相当于给梯度加上了一个动量，让它在局部最小值点或者鞍点上不会轻易停下来。
在每一次计算速度上，都要加上一个rho系数，也就是摩擦系数，让上一次的速度乘以0.9再加上这次新的梯度，综合来看，每一次的速度值都是之前所有梯度的加权和，越近的梯度权重越大，越久远的梯度权重越小。所以可以把它看成一个最近梯度平均的平滑移动。
另一种有轻微变化的叫Nesterov Momentum会在速度方向上重新选择步进值。

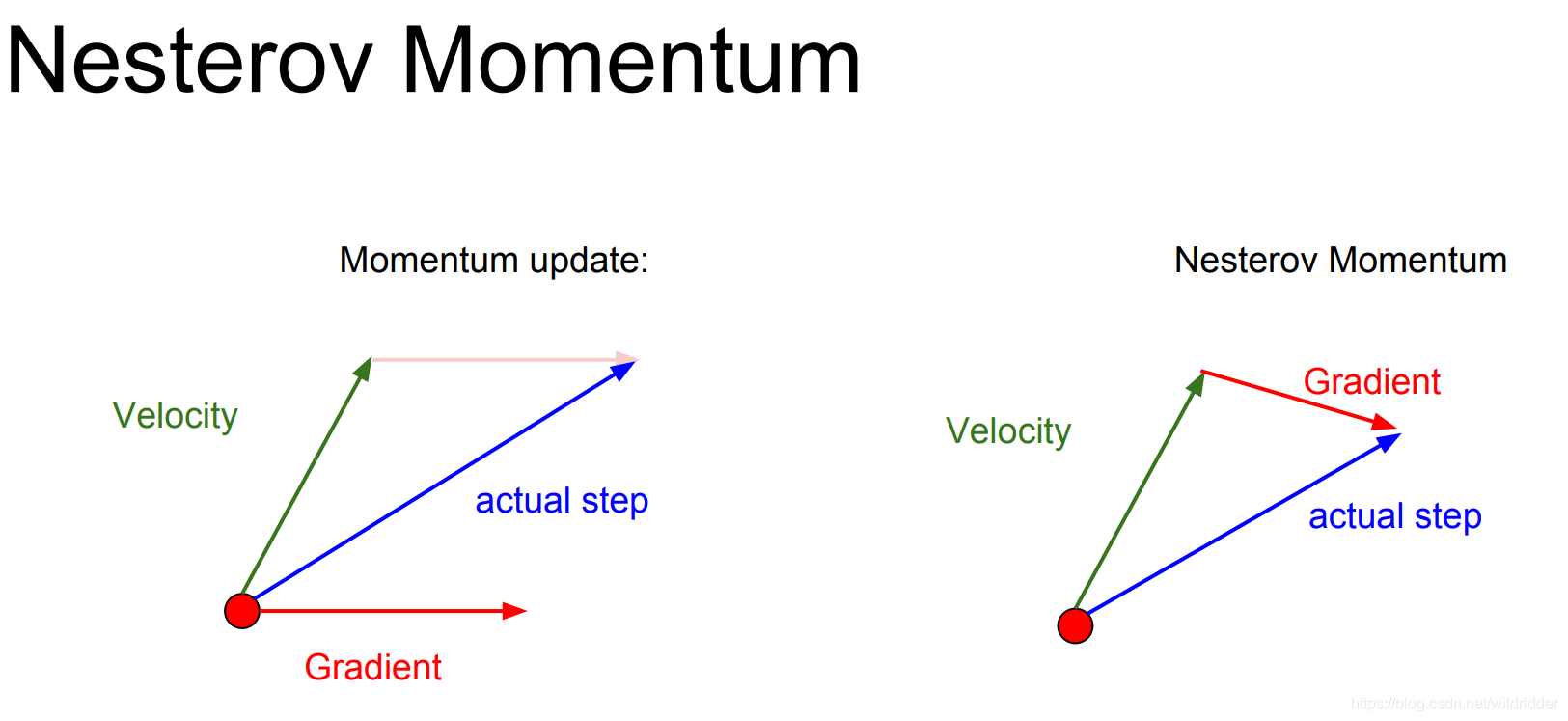
由于Nesterov有校正因子的存在，他不会那么剧烈越过局部极小值点。

AdaGrad优化算法

保持计算每一步的梯度平方和的持续估计，训练时会一直持续叠加当前梯度的平方和到这个梯度平方项，当我们在更新我们的参数向量时，我们会除以这个梯度平方项
所以使用AdaGrad的时候步长会变得越来越小，在学习目标是一个凸函数时，这个特征效果很好，因为当快到达极值点时会逐渐慢下来最后到达收敛，但是在非凸函数情况下，当到达一个局部极值点时AdaGrad会让训练在这里被困住。
所以对AdaGrad有一个变体叫RMSProp

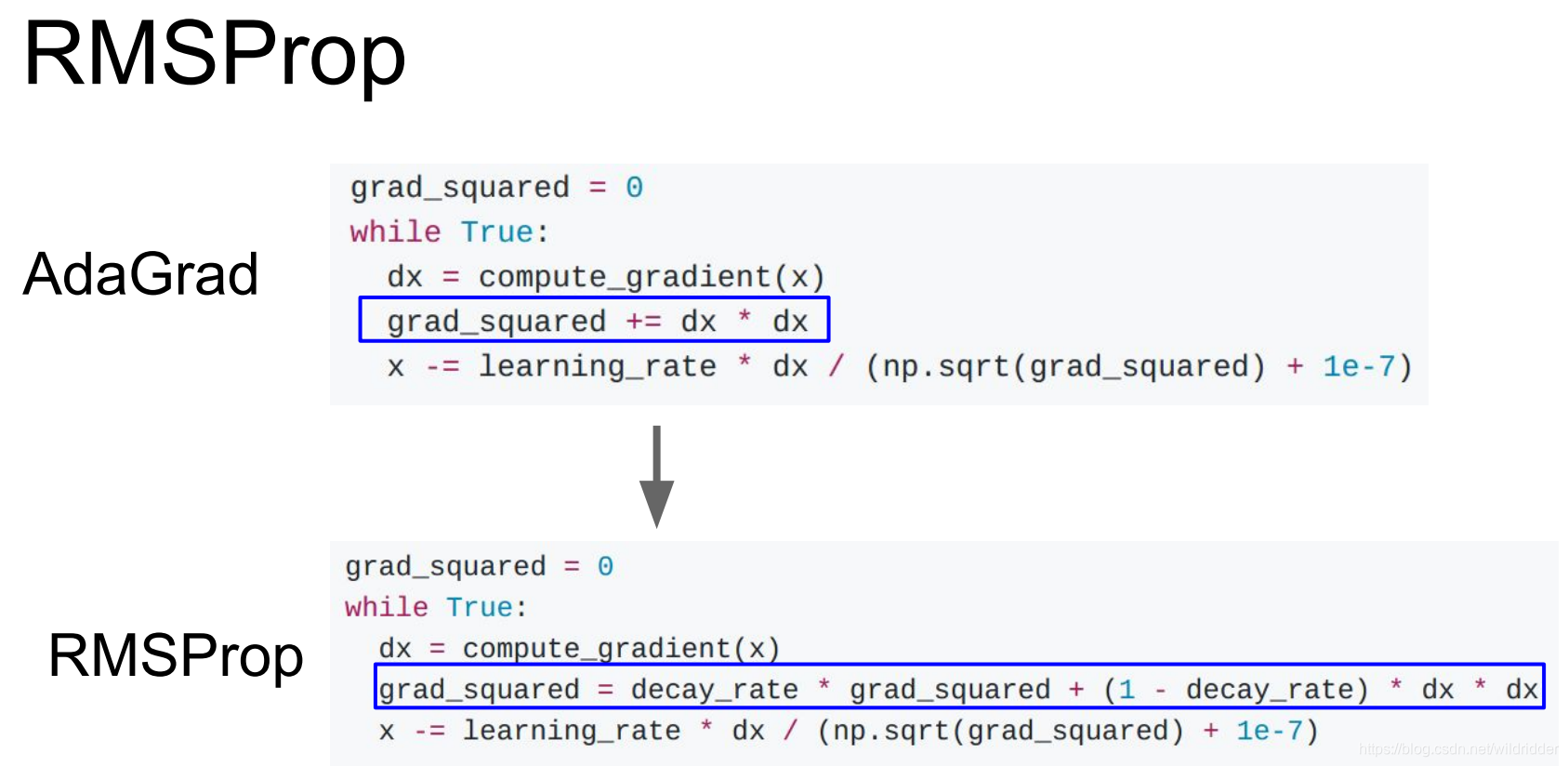
在RMSProp里并不是单纯的叠加梯度的平方，而是会让平方梯度按照一定比率下降

Adam算法

Adam算法是Momentum和RMSProp的合体，

因为人为的将第二动量second_moment初始化为0，第一步算出的第二动量值很小很小，导致x步长一开始就非常非常大。所以完整版的Adam增加了偏置校正项，避免出现开始时得到很大步长:

Adam对任何问题基本都有不错的表现，所以遇见新的问题时可以先尝试用Adam，特别是如果将beta1设置为0.9，beta2设置为0.999，学习率设置为1e-3，无论使用什么网络构架基本都能很好的开始。