FDA-BP多输入回归|流向优化算法-BP神经网络|Matlab

目录

一、程序及算法内容介绍：

基本内容：

亮点与优势：

 二、实际运行效果：

三、方法原理介绍：

算法原理：

数学模型和参数设置：

四、完整程序下载：

---

一、程序及算法内容介绍：

基本内容：

• 本代码基于Matlab平台编译，将FDA(流向优化算法)与BP神经网络结合，进行多输入数据回归预测。(多变量回归预测，个数可自行指定)

• 输入训练的数据包含7个特征，1个响应值，即通过7个输入值预测1个输出值。（数据导入后自动归一化，提升泛化性）

• 通过FDA算法优化BP的初始权重、初始偏差参数，记录下最优的网络参数

• 迭代计算过程中，自动显示优化进度条，实时查看程序运行进展情况

• 自动输出多种多样的的误差评价指标，自动输出大量实验效果图片

亮点与优势：

• 注释详细，几乎每一关键行都有注释说明，适合小白起步学习

• 直接运行Main函数即可看到所有结果，使用便捷

• 编程习惯良好，程序主体标准化，逻辑清晰，方便阅读代码

• 所有数据均采用Excel格式输入，替换数据方便，适合懒人选手

• 出图详细、丰富、美观，可直观查看运行效果

• 附带详细的说明文档（下图），其内容包括：算法原理+使用方法说明

 二、实际运行效果：

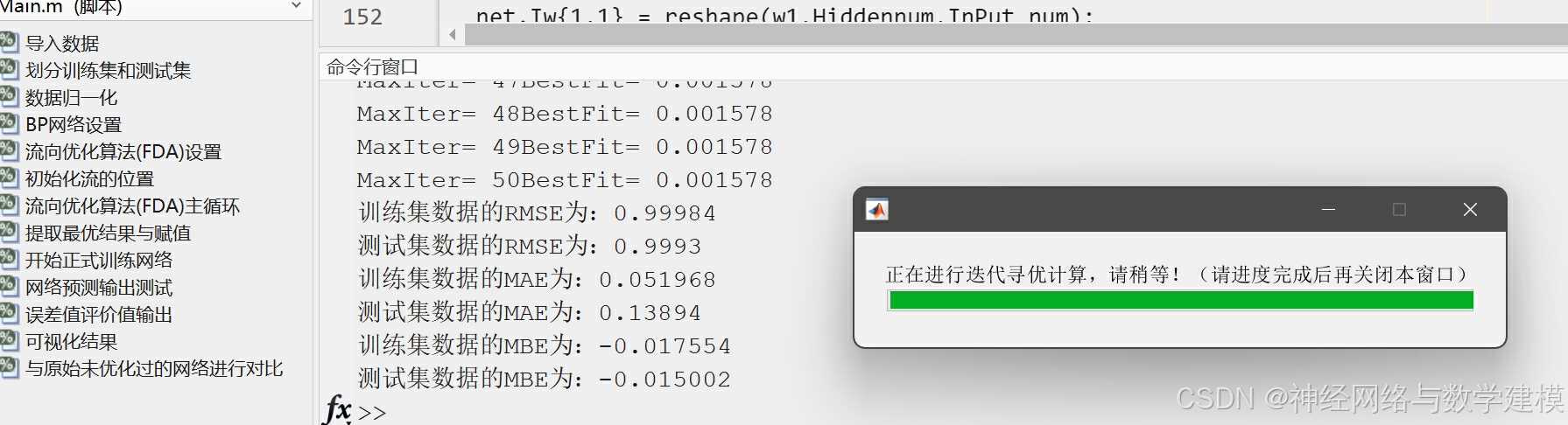
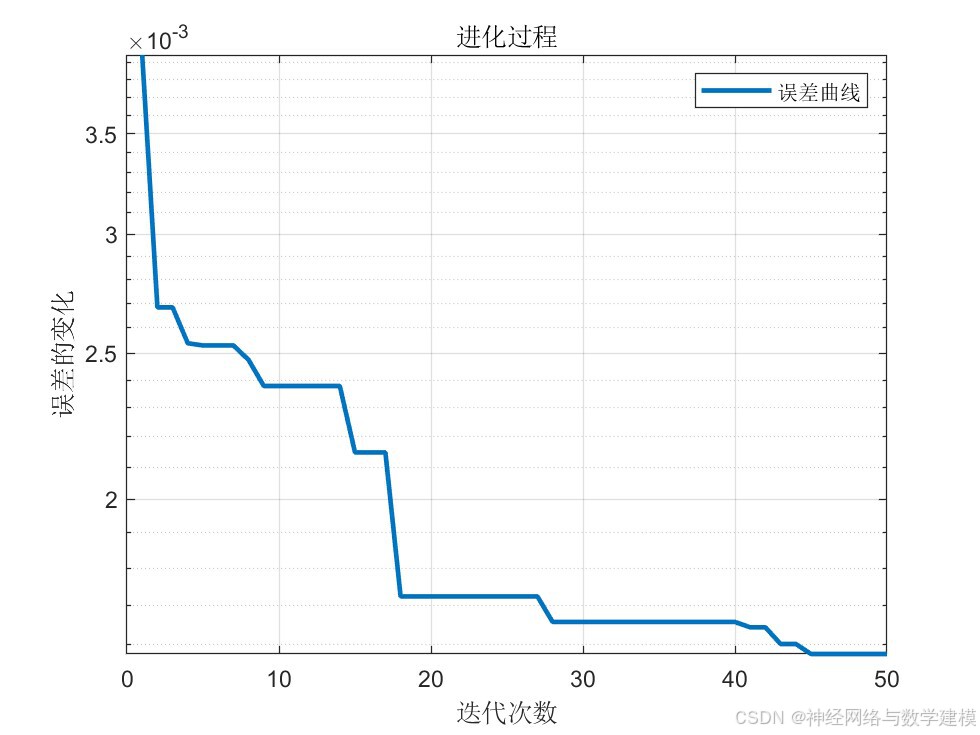
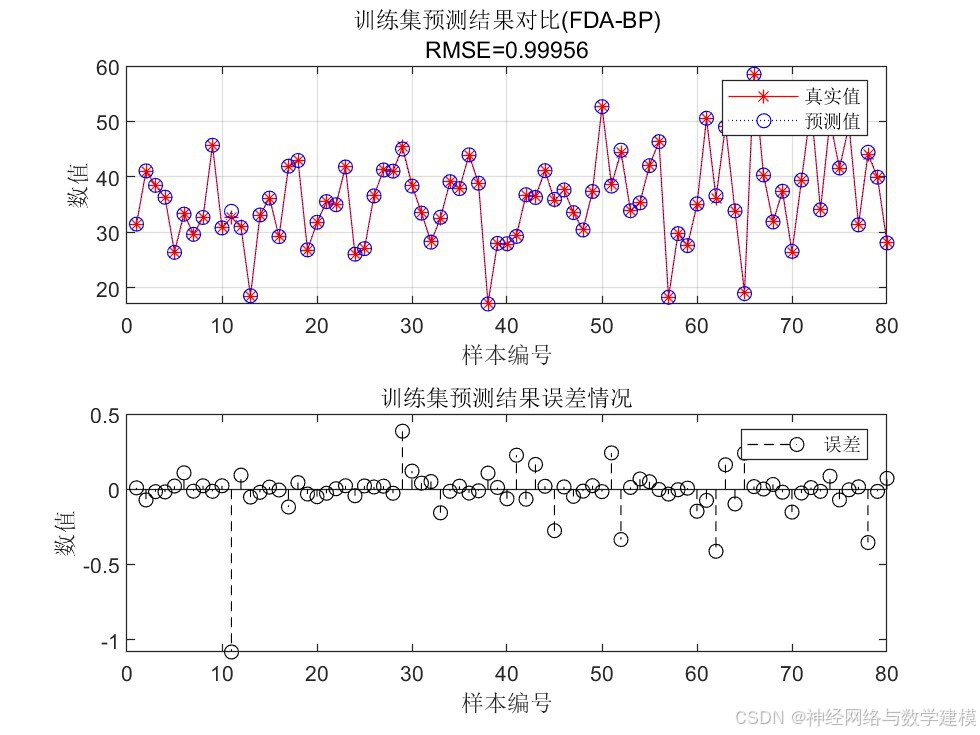
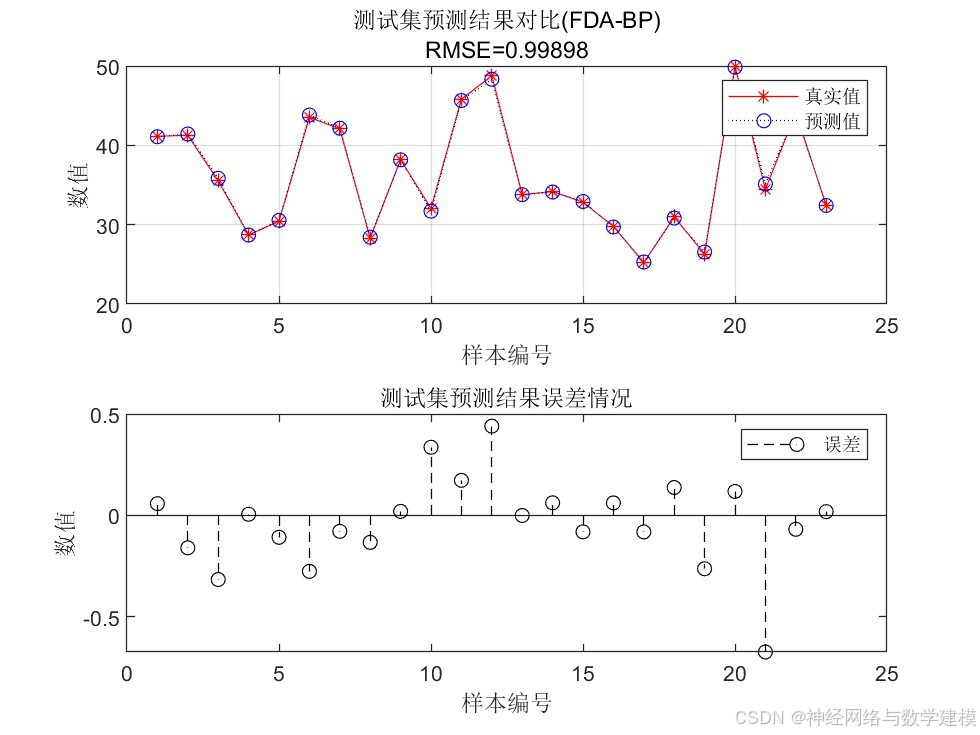
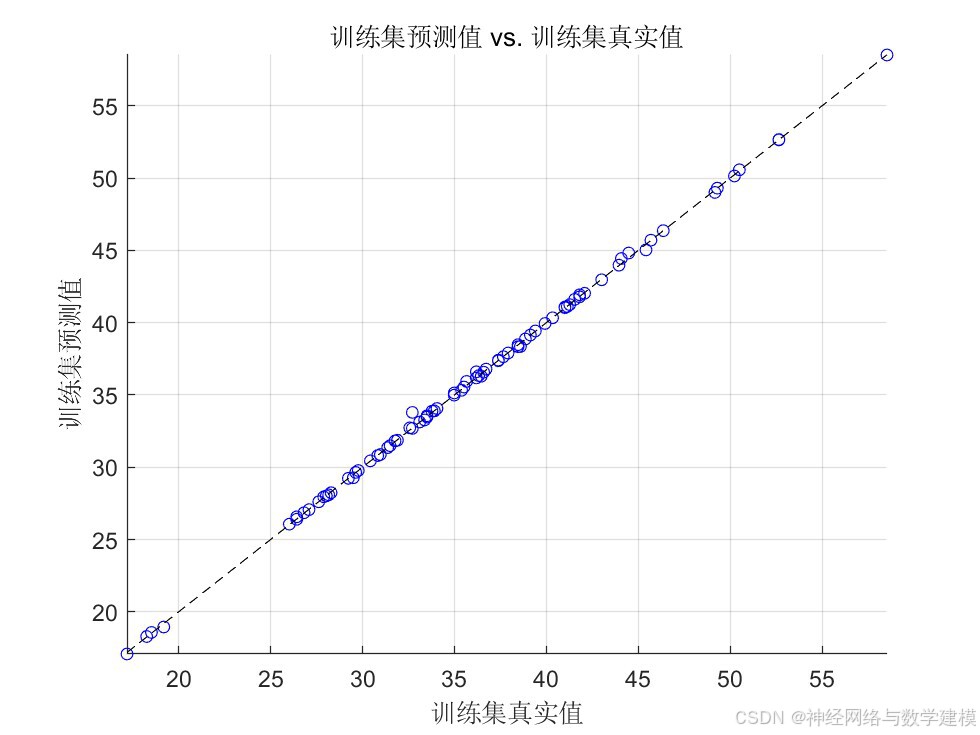
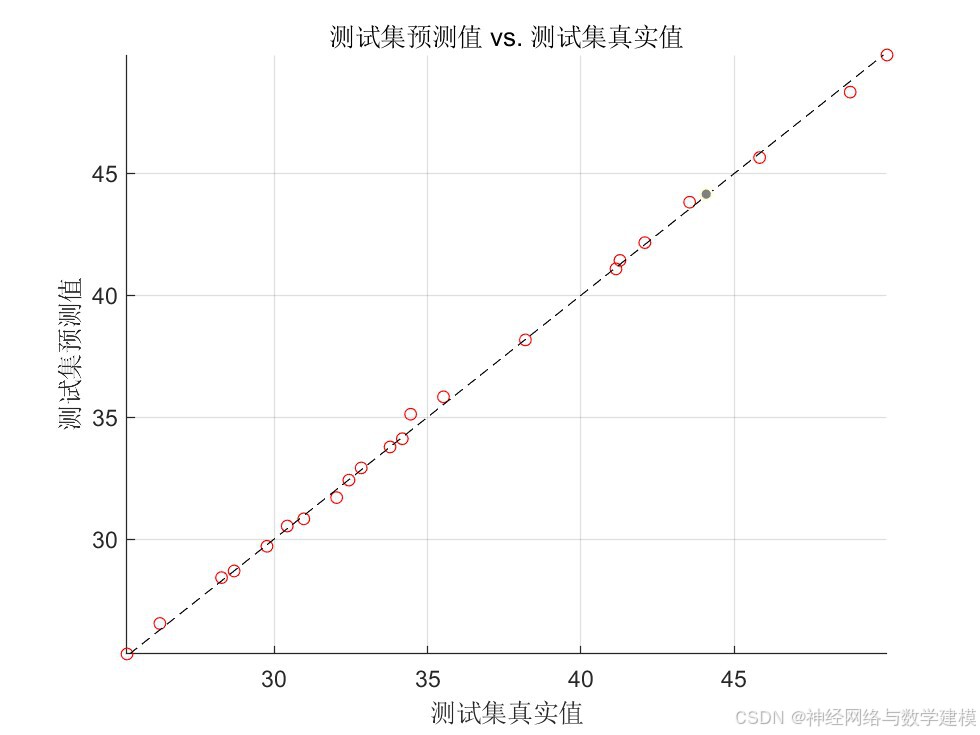
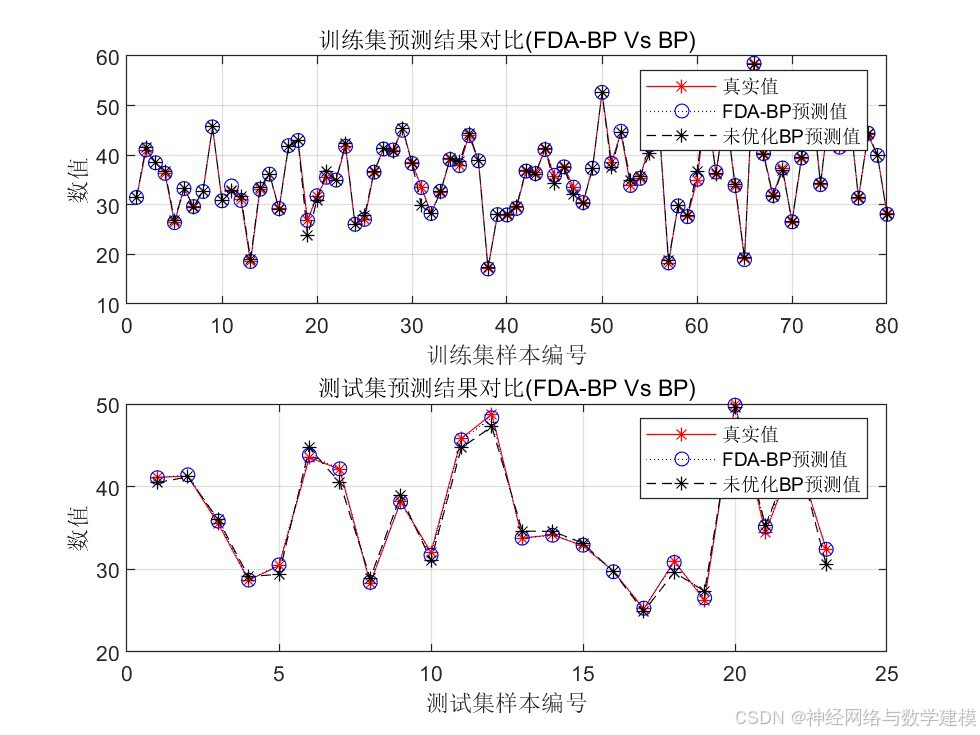
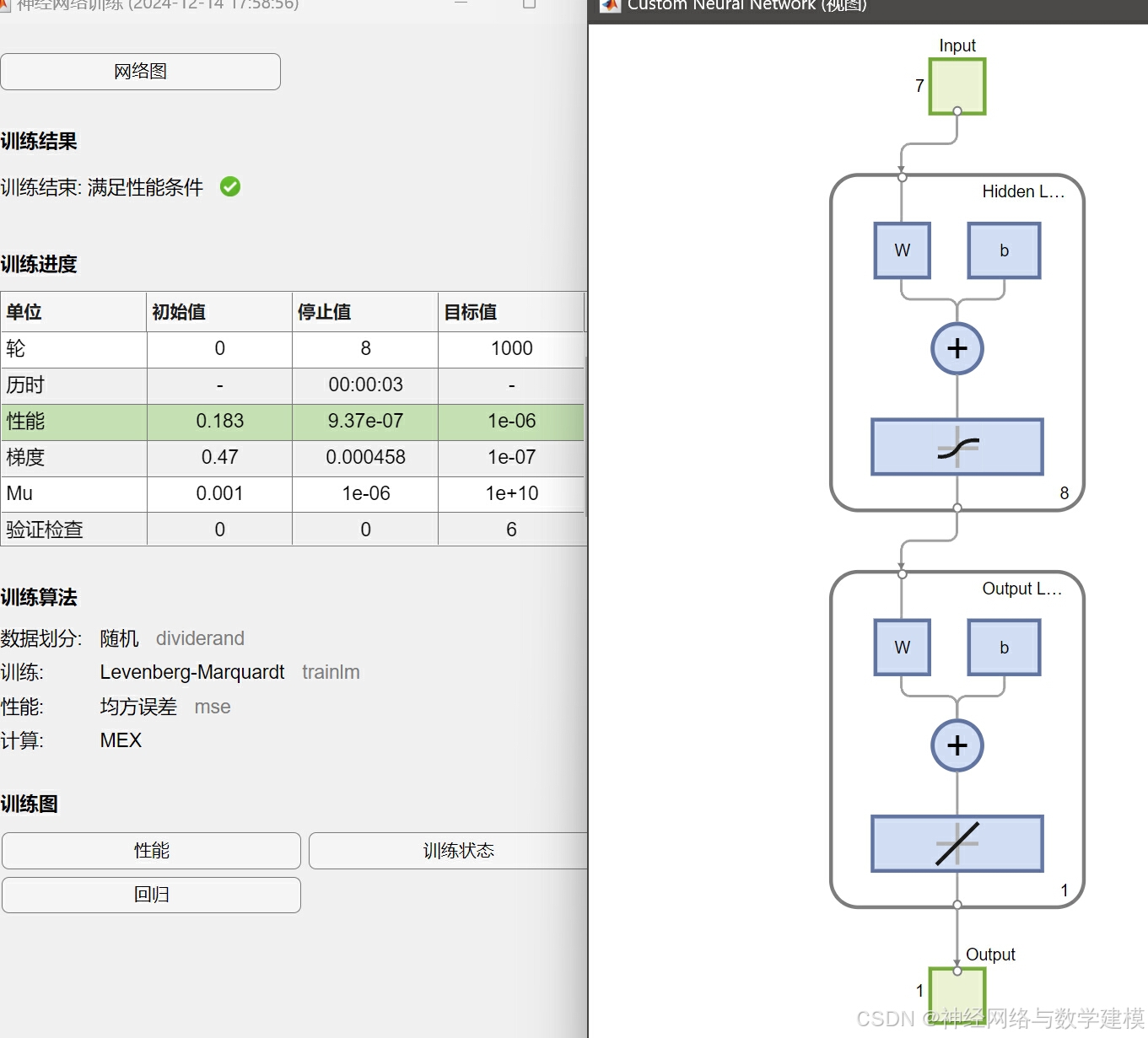
三、方法原理介绍：

‌流向优化算法（Flow Direction Algorithm，FDA）是一种基于物理的优化算法，其灵感来源于水流运动规律。‌ FDA模拟了水流朝向最低海拔出口流动的过程，通过模拟水流在搜索空间中的运动来寻找最优解。算法的核心思想是将优化问题转化为水流在搜索空间中的流动问题，水流会朝向海拔最低的位置流动，从而达到优化目标‌。

算法原理：

FDA通过以下几个步骤实现优化：

• ‌创建初始种群‌：在搜索空间中创建一个初始种群，每个“水流”代表一个潜在的解。

• 考虑邻域影响‌：每个水流周围存在一定数量的邻域，水流会受到邻近水流及其坡度的影响。

• ‌更新水流位置‌：水流会朝向海拔较低的位置移动，即朝向目标函数值更优的方向流动。

• ‌结果展示‌：通过多次迭代，最终找到海拔最低的位置，即最优解‌。

数学模型和参数设置：

FDA的数学模型包括以下几个关键参数：

• 邻域数量β‌：每个水流周围存在的邻域数量。

• 控制参数Δ‌：用于控制搜索空间的大小，其值从一个较大值线性减小到较小值。

• 非线性权重W‌：用于调整搜索过程中的权重，影响搜索范围和多样性‌。

四、完整程序下载：