[JavaScript数据结构] 栈的实现及应用

开始

栈是一种特殊的线性表，仅能够在栈顶进行操作，有着先进后出的特性。下面这张图为栈的工作特点：

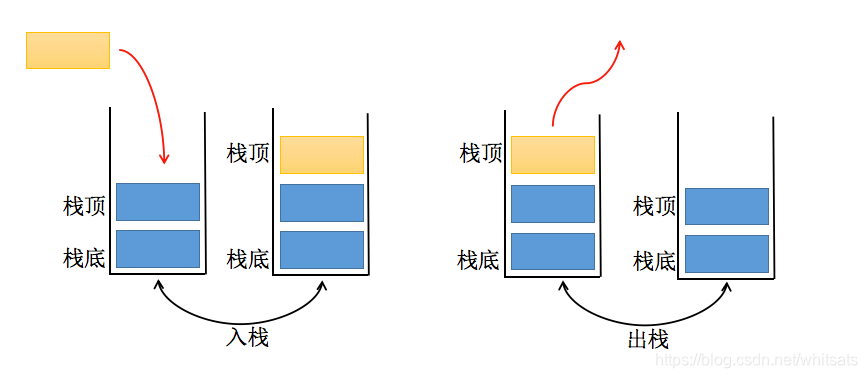
从数据存储的角度看，用JavaScript实现栈有两种方式，一种是以数组做基础，一种是以链表做基础，本节中，我们使用数组实现栈。链表会作为单独的数据结果进行介绍。

我们先定义一个简单的Stack类

function Stack(){
	var items = []; // 用数组存储数据
}

数据会存储在 items数组中，现在，这个类没有任何的方法。

栈的方法

栈的方法有以下几种

• push 添加一个元素到栈顶
• pop 弹出栈顶的元素
• top返回栈顶的元素
• isEmpty 判断栈是否为空
• size返回栈里的元素个数
• clear 清空栈

下面我们来逐一实现这些方法。

push 方法

function Stack(){
	var items = []; // 用数组存储数据
	this.push = function(item){
		items.push(item); // 压栈
	}
}

pop方法

function Stack(){
	var items = []; // 用数组存储数据
	this.push = function(item){
		items.push(item); // 压栈
	}
	this.pop = function(){
		return items.pop()
	}
}

top方法

function Stack(){
	var items = []; // 用数组存储数据
	this.push = function(item){
		items.push(item); // 压栈
	}
	this.pop = function(){
		return items.pop()
	}
	this.top = function(){
		return items[items.length - 1];
	}
}

isEmpty 方法

function Stack(){
	var items = []; // 用数组存储数据
	this.push = function(item){
		items.push(item); // 压栈
	}
	this.pop = function(){
		return items.pop()
	}
	this.top = function(){
		return items[items.length - 1];
	}
	this.isEmpty = function(){
		return items.length === 0;
	}
}

size 方法

function Stack(){
	var items = []; // 用数组存储数据
	this.push = function(item){
		items.push(item); // 压栈
	}
	this.pop = function(){
		return items.pop()
	}
	this.top = function(){
		return items[items.length - 1];
	}
	this.isEmpty = function(){
		return items.length === 0;
	}
	this.size = function(){
		return items.length;
	}
}

clear 方法

function Stack(){
	var items = []; // 用数组存储数据
	this.push = function(item){
		items.push(item); // 压栈
	}
	this.pop = function(){
		return items.pop()
	}
	this.top = function(){
		return items[items.length - 1];
	}
	this.isEmpty = function(){
		return items.length === 0;
	}
	this.size = function(){
		return items.length;
	}
	this.clear = function(){
		items = [];
	}
}

我们使用var items = []的原因是，我们要将items封闭在类的内部，不能暴露出来。需要将items封装成似有属性。

	function Stack(){
		this.items = [];
	}
	var stack = new Stack();
	// 可以直接通过实例修改类的属性。
	stack.items.push(3);

被欺骗的感觉

看完上面的实现，读者可能会有一种被欺骗的感觉，传的那么神乎其神的数据结构，这里实现的栈，竟然只是对数组做了一层封装！

请大家思考下面几个问题

1. 我们可以通过索引操作数组的任意元素，但是这个栈，我们能操作任意元素吗？栈提供的方法只允许你操作栈顶的元素，也就是数组的最后一个元素，这种限制给了我们一种思考问题的方式。
2. 既然栈的底层实现就是数组，栈能做的事情数组也可以一样做，为什么弄一个栈出来，是不是多此一举呢？其实，封装是为了隐藏实现的细节，在栈的角度思考问题会更为方便。

栈的应用练习

通过以下两个练习，我们能够更为清晰的明白，从栈的角度思考问题更为方便。

合法括号

题目要求

下面的字符串中包含小括号，请编写一个函数判断字符串中的括号是否合法，所谓合法，就是括号成对出现。

sdf(ds(ew(we)re)rwqw)qwrwq		合法
(sd(qwqe)sd(sd))		合法
()()sd()(sd()dw))(		不合法

思路分析

括号存在嵌套关系，也存在并列关系，如果使用数组来存储这些括号，然后再想办法一对一的抵消掉，似乎可行。但是我们无法判断一个左括号对应的是哪一个右括号。在数组的角度思考这个问题，就有些困难。

现在，我们使用栈来解决这个问题

• 遇到左括号，就把做括号压入栈中
• 遇到右括号，判断栈是否为空，如果为空则说明没有左括号与之相对应，字符串括号不合法。如果栈不为空，则把栈顶元素移除，这对括号就抵消了。
  当for循环结束，如果栈是空的，说明所有的左右括号都抵消了，如果栈力还有元素，则说明缺少右括号，字符串括号不合法。

示例代码

function is_leagl_brackets(string){
	var stack = new Stack();
	for (var i = 0;i<string.length;i++) {
		var item = string[i];
		// 遇到做括号入栈
		if(item == '('){
			stack.push(item)
		}else if (item == ')'){
		// 遇到右括号，判断栈是否为空
			if(stack.isEmpty()){
				return false
			}else {
				stack.pop() // 弹出左括号
			}
		}
	}
	//  如果栈为空，说明字符串括号合法
	return stack.isEmpty()
}
console.log(is_leagl_brackets('sdf(ds(ew(we)re)rwqw)qwrwq')) // true
console.log(is_leagl_brackets('(sd(qwqe)sd(sd))')) // true
console.log(is_leagl_brackets('()()sd()(sd()dw))(')) // false

小结

栈的底层是不是使用了数组并不重要，重要的是栈的这种后进先出的特性。重要的是你只能操作栈顶的元素的限制。一定要忽略栈的底层实现，而关心栈的特性。

计算逆波兰表达式

题目要求

逆波兰表达式，也叫后缀表达式，它将复杂的表达式转换为可以依靠简单的操作得到计算结果的表达式。例如(a+b)*(c+d)转换成为ab+cd+*

示🌰

[“4”,“13”,'5','/','+'] 等价于 (4+(13/5)) = 6
['10','6','9','3','-11','*','/','*','17','+','5','+'] 等价于((10*(6/((9+3)*-11)))+17) + 5

请编写函数calc_exp(exp)实现逆波兰表达式，其中exp的类型是数组。

后缀变中缀
[“4”,“13”,‘5’,’/’,’+’] --> [“4”,‘2’,’+’] --> 6

思路分析

[“4”,“13”,'5','/','+'] 就是一个数组，如果使用数组来解决这个问题，遇到/时，取出13和5进行计算，然后将这两者删除，把计算结果放到4的后面，书写算法会过于麻烦。

如果是栈来解决这个问题，就会变得简单而自然。使用for循环遍历数组，对每一个数组元素进行如下操作

• 如果元素不是 + - * /的其中一个，就压入栈中。
• 如果元素是+ - * /中的一个，就从栈中连续弹出两个元素，并对这两个元素进行计算，将结果压入栈中

for循环结束之后，栈里只有一个元素，这个元素就是整个表达式的计算结果。

示例代码

function calc_exp(exp) {
	var stack = new Stack()
	for (var i = 0;i<exp.length; i++) {
		var item = exp[i];
		if (['+','-','*','/'].indexOf(item) >= 0) {
			var val_1 = stack.pop()
			var val_2 = stack.pop()
			var exp_str = val_2 + item + val_1;
			console.log(exp_str)
			// 计算并取整
			var res = parseInt(eval(exp_str));
			// 计算结果压入栈中
			stack.push(res.toString())
		}else {
			stack.push(item)
		}
	}
	return stack.pop()
}

console.log(calc_exp(['4','13','5','/','+'])) // 6

拓展：实现一个有min方法的栈

实现一个栈，除了常见的push和pop方法意外，提供一个min方法，返回栈里的最小的元素，且时间复杂度为O(1)

function MinStack() {
	var data_stack = new Stack();
	var min_stack = new Stack();
	// 用min_stack 记录每次 push 进来的元素之后，栈中的最小值
	this.push = function (item) {
		data_stack.push(item);
		if(min_stack.isEmpty() || item < min_stack.top()){
			min_stack.push(item)
		}else {
			min_stack.push(min_stack.top())
		}
	};
	// 这样，每次pop之后，min_stack 也会将上次栈中的最小值弹出
	this.pop() = function () {
		data_stack.pop()
		min_stack.pop()
	}
	this.min = function () {
		return min_stack.top()
	}
}

拓展：实现中缀转后缀表达式

输入：(1 + (4+5+3) -3) + (9+8)
输出: ['1','4','5','+','3','+','+','3','-','9','8','+','+'] 

// 运算符优先级
var priority_map = {
	"+":1,
	"-":1,
	"*":2,
	"/":2
}
function infix_exp_2_postfix_exp(exp) {
	var stack = new Stack()
	var postfix_list = []
	for (var i = 0;i<exp.length;i++) {
		var item = exp[i];
		// 如果是数字，则直接放入 post_fix_list中
		if(isNaN(item)){
			postfix_list.push(item)
		// 遇到左括号入栈
		}else if (item == "("){
			stack.push(item)
		// 遇到右括号，把栈顶元素弹出，直到遇到左括号
		}else if (item == ')') {
			while (stack.top() != "(") {
				postfix_list.push(stack.pop())
			}
			// 左括号出栈
			stack.pop()
		}else{
			// 遇到运算符，把栈顶运算符弹出，直到栈顶的运算符的优先级小于当前运算符
			while (!stack.isEmpty()&&['+','-','*','/'].indexOf(stack.top())>=0 && priority_map[stack.top()] >= priority_map[item]) {
				postfix_list.push(stack.pop())
			}
			stack.push(item)
		}
	}
	// for 循环结束后，栈里可能还有元素，都弹出放入到postfix_list当中
	while (!stack.isEmpty()) {
		postfix_list.push(stack.pop())
	}
	return postfix_list
}