贝叶斯网

最新推荐文章于 2024-04-24 14:45:38 发布
原创 最新推荐文章于 2024-04-24 14:45:38 发布 · 490 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文深入探讨了贝叶斯网的结构、学习及推断过程，详细介绍了其如何利用有向无环图表达属性间依赖关系，通过条件概率表描述联合概率分布，以及在未知网络结构情况下的学习策略和采用吉布斯采样的推断方法。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

       贝叶斯网借助有向无环图(Directed Acyclic Graph ，简称 DAG)来刻画属性之间的依赖关系，并使用条件概率表(Conditiona Probability Table 简称 CPT）来描述属性的联合概率分布。

  • 结构

贝叶斯网有效的表达了属性间的条件独立性。它假设每一个节点与和该节点“没有亲缘关系”的节点独立。定义联合概率分布

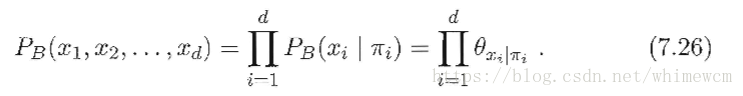
接下来的道德图根据图论中的连通分支概念应该会很好理解。

  • 学习

若在已知贝叶斯网的网络结构的情况下，学习过程只需对样本进行计数，估计出每个节点的条件概率表即可。通常我们并不知晓网络结构，我们定义一个评分函数，用来评估结构最优的贝叶斯网。（有点类似哈夫曼树）

 

 

  • 推断

贝叶斯网的推断常采用一种随机采样方法——吉布斯采样来完成。

 

动态贝叶斯网络DBN
tanzhangwen的专栏
12-05 3万+
贝叶斯网络 贝叶斯网络（Bayesian Networks）也被称为信念网络（Belif Networks）或者因果网络（Causal Networks），是描述数据变量之间依赖关系的一种图形模式，是一种用来进行推理的模型。贝叶斯网络为人们提供了一种方便的框架结构来表示因果关系，这使得不确定性推理变得在逻辑上更为清晰、可理解性强。对于贝叶斯网络，我们可以用两种方法来看待它：首先贝叶斯网表达了各个节
贝叶斯网络
qq_32172681的博客
09-21 6793
1、概念 贝叶斯网络(Bayesian network)，或称有向无环图模型，是一种概率图模型。 贝叶斯网络的有向无环图中的节点表示随机变量， 它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件...
Machine Learning机器学习之贝叶斯网络(BayesianNetwork)
a910247的博客
03-28 1万+
贝叶斯网络（Bayesian Network），也称为信念网络（Belief Network）或概率有向无环图（Probabilistic Directed Acyclic Graph，PDAG），是一种用图形表示概率模型的方法，它基于概率推断的贝叶斯定理。贝叶斯网络的背景可以追溯到 1980 年代初期，它是由一些著名的人工智能研究者如Judea Pearl、Peter Spirtes、Clark Glymour等提出和发展起来的。
机器学习：贝叶斯网络
JacksonKim的博客
11-27 1万+
贝叶斯网络
静态、动态贝叶斯网络-GeNIe软件建模 贝叶斯网络模型建立指导:包括条件概率表(CPT)的设定方法(二态或者多状态均可)，软件的使用方法动态贝叶斯网络，分析方法等 如何构建贝叶斯的结构，以及如何
最新发布
03-14
贝叶斯网络是一种基于概率推理的图形化模型，它能够对不确定性进行推理、学习和预测，广泛应用于风险评估、决策支持、数据挖掘等领域。GeNIe软件是支持贝叶斯网络建模与分析的工具之一，它具备直观的图形界面，方便...
贝叶斯网络java代码及训练集测试集_贝叶斯网络_测试集_
10-01
贝叶斯网络是一种概率图模型，它在统计学和机器学习领域中被广泛使用，用于表示变量之间的条件概率关系。这种网络基于贝叶斯定理，可以用来进行预测分析、分类、诊断和推理等任务。在Java编程环境中实现贝叶斯网络，...
贝叶斯网络GeNIe软件安装包-academic版本-4.1.3402版本
12-21
**贝叶斯网络与GeNIe软件** 贝叶斯网络是一种概率图模型，它在人工智能、统计学和机器学习领域中扮演着重要角色。这种网络通过节点和边来表示随机变量及其条件概率关系，能够有效地处理不确定性问题。贝叶斯网络的...
贝叶斯网络20题目.docx
07-20
"贝叶斯网络20题目.docx" 本资源是贝叶斯网络学习的习题集，共20道，涵盖贝叶斯网络的基本概念、公式、理论和应用。下面是对每个知识点的详细解释： 1.贝叶斯公式：P(B|A) = P(A|B) \* P(B) / P(A)，其中M=P(AB)/P...
贝叶斯网络 详解
09-11
全概率分布可以回答相关领域的任何问题，但随着变量数目的增 加，全概率分布的联合取值空间却可能变得很大。另外，对所有的原 子事实给出概率，对用户来说也非常困难。 若使用Bayes 规则，就可以利用变量之间的条件独立关系简化计 算过程，大大降低所需要声明的条件概率的数目。我们可以用一个叫 作Bayesian 网的数据结构来表示变量之间的依赖关系，并为全概率分 布给出一个简明的表示。 定义（Bayesian 网）：Bayesian 网T 是一个三元组（N,A,P）,其 中 1． N 是节点集合 2． A 是有向弧集合，与N 组成有限非循环图G =（N，A） 3． P {p(V | ) :V N} v    ，其中 v  代表节点V 的父亲节点集合 Bayesian 网是一个有向非循环图： （1） 网中节点与知识领域的随机变量一一对应（下文中不区分节 点与变量）； （2）网中的有向弧表示变量间的因果关系，从节点X 到节点Y 有 向弧的直观含义是X 对Y 有直接的因果影响；影响的强度或者说不确 定性由条件概率表示； （3）每个节点有一个条件概率表，定量描述其所有父亲节点对于 该节点的作用效果。 -2- （4）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 ）由领域专家给定网络结构和条件概率表。 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 对领域专家来说，决定在特中存哪些条件独立联系通常是 较容易的 较容易的 较容易的 （给定网络结构相对容易 给定网络结构相对容易 给定网络结构相对容易 给定网络结构相对容易 给定网络结构相对容易 ）─ 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 事实上，要远比际声明出这 些概率本身容易得多 些概率本身容易得多 些概率本身容易得多 些概率本身容易得多 些概率本身容易得多 （给定准确的条件概率相对 给定准确的条件概率相对 给定准确的条件概率相对 给定准确的条件概率相对 给定准确的条件概率相对 给定准确的条件概率相对 困难） 。一旦 。一旦 。一旦 BayesianBayesianBayesianBayesianBayesian Bayesian网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网的拓扑结构给定， 则只需对那些直接相互依赖节点出条件概率网
机器学习——贝叶斯网(bayesian Network)一
Roswell的博客
08-26 2万+
把某个研究系统按照设计的随机变量,感觉是否条件独立绘制在一个有向图中,这就近形成了贝叶斯网络. 贝叶斯网络一个有向无环图(Directed Acyclic Graph,DAG),是一种概率图模型,根据概率图的拓扑结构,考察一组随机变量{x1x2,x3......xn}即其n组的条件概率分布(Conditional Probability Distributions,CPD)的性质. 其中有向无...
贝叶斯网络详解
热门推荐
weixin_43211186的博客
06-24 3万+
有时我们需要计算一个不确定原因的概率给出一些观察到的证据，在这些情况下可以使用贝叶斯方法。 贝叶斯网络（bayesian network） 是一种概率图形模型，它在图形模型中显式捕获已知的有向边的条件依赖性，它通过有向无环图(DAG)表示一组变量及其条件依赖关系。贝叶斯网络非常适合用于获取已发生的事件并预测几种可能的已知原因中的任意一种。例如，贝叶斯网络可以表示疾病和症状之间的概率关系。给定症状，该网络可用于计算各种疾病存在的概率。高效的算法可以在贝叶斯网络中进行推理和学习。 对变量序列（例如 语音信号或蛋
Advanced Topics in Statistical Machine Learning 笔记02：贝叶斯网络（Bayesian Network）
MYJace的博客
10-03 2618
Advanced Topics in Statistical Machine Learning 笔记02：贝叶斯网络
贝叶斯信念网络
Forlogenの解忧杂货铺
04-12 3093
回顾 贝叶斯定理 贝叶斯定理是计算概率中很重要也是很常用的一个公式，它的形式如下： p(Yk∣X)=P(XYk)P(X)=P(Yk)p(X∣Yk)∑jP(Yj)P(X∣Yj) p(Y_{k}|X)=\frac{P(XY_{k})}{P(X)}=\frac{P(Y_{k})p(X|Y_{k})}{\sum_{j}P(Y_{j})P(X|Y_{j})} p(Yk​∣X)=P(X)P(XYk​)​=∑...
Machine Learning-L17-贝叶斯网络
聚集机器学习、信息安全
05-02 2254
贝叶斯网络（Bayesian network）又称信念网络（belief network），使用有向无环图（Directed Acyclic Graph）来表示变量间的依赖关系，并使用条件概率表（CPT，Conditional Probability Table）描述属性的联合概率分布。
贝叶斯网络（概念、应用、实例）
weixin_47151388的博客
04-24 1万+
在贝叶斯网络中，每个节点都有一个与之相关的条件概率表（Conditional Probability Table, CPT），该表描述了在给定父节点状态下该节点状态的概率分布。： 贝叶斯网络可以应用于推荐系统中，通过分析用户的历史行为和偏好，预测用户可能感兴趣的新产品或服务。： 在生物信息学和医学研究中，贝叶斯网络可以用来发现变量之间的潜在关系，如基因表达数据中的调控网络。贝叶斯网络在机器学习中的应用十分广泛，它能够提供强大的框架来处理具有不确定性和复杂依赖关系的数据。
贝叶斯网络: 概率图模型的强大工具
AI天才研究院
12-29 1611
1.背景介绍 贝叶斯网络(Bayesian Network)，也被称为贝叶斯条件依赖网络(Bayesian Causal Network)或简称为有向无环图(DAG)，是一种概率图模型，用于表示和推理随机事件之间的概率关系。贝叶斯网络是基于贝叶斯定理的一种推理方法，它可以用来表示和推理随机事件之间的概率关系。贝叶斯网络的主要优势在于它可以有效地处理不完全观测数据和不确定性，并在许多领域得到广泛应...
机器学习笔记之贝叶斯分类器贝叶斯网络
sibiantai555的博客
04-07 569
来来来 总结下 上一节课的贝叶斯参数估计，你会发现一个相当有意思的事情就是要后验概率必须满足以下三个条件：（1）一定要通过先验知识假设θ的密度函数（2）而且样本是相互独立的（3） 你要假设未知数的概率密度函数以及总体其服从的分布嗯哼哼 傻了吧 那么多先决条件 要利用贝叶斯算法做一个分类器真难首先来确定贝叶斯分类器设计的基本思想通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类...
贝叶斯网络基础与应用
"该资源是关于贝叶斯网络的英文介绍，包含了一些实施注解，列举了不同领域如电力、电信、航空旅行等的状态概率分布。" 贝叶斯网络（Bayesian Networks），又称为信念网络或贝叶斯信念网络，是一种在概率推理中广泛...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值