装袋（Bagging）过程

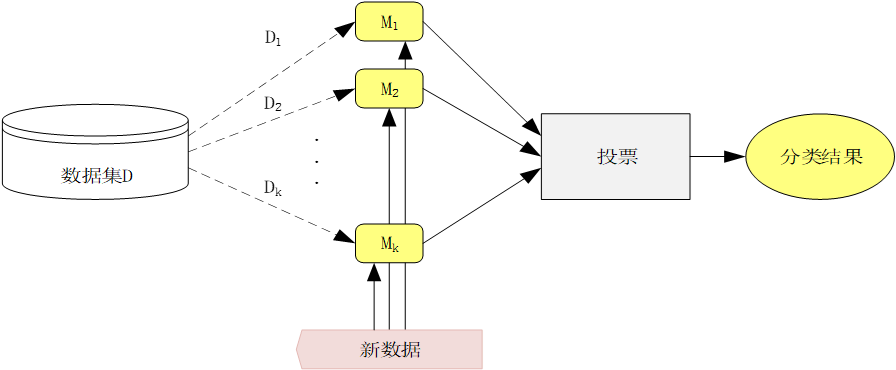
咱们结合这张图，用 “选水果” 的例子，bb装袋（Bagging）的过程：

1. 数据集 D：“水果仓库”

假设图里的 “数据集 D” 是一个大仓库，里面有 100 个水果（有苹果、梨、桃子等），每个水果都标好了 “是不是苹果” 的标签。

2. 抽子集 D₁、D₂…Dₖ：“多次随机抽水果”

装袋的第一步，是从这个仓库里 **“有放回地” 抽水果 **：

1. 第一次抽 100 个（比如抽到 50 个苹果、30 个梨、20 个桃子），组成子集 D₁；
2. 第二次再抽 100 个（可能又抽到 40 个苹果、40 个梨、20 个桃子），组成子集 D₂；
3. 重复 k 次，得到 k 个子集（比如 k=5，就有 D₁到 D₅五份不同的水果样本）。

注意：“有放回” 意味着同一个水果可能被多次抽到，这样每个子集的水果分布会略有不同，让后面的模型学出不同的规律。

3. 训练模型 M₁、M₂…Mₖ：“5 个评委各自学习”

把每个子集 D₁到 D₅，分别交给 5 个 “评委”（模型 M₁到 M₅）学习：

1. M₁用 D₁学：比如它学到 “红的、圆的、重 150g 左右是苹果”；
2. M₂用 D₂学：它可能学到 “红的、甜的、产自山东是苹果”；
3. ……
4. M₅用 D₅学：它可能学到 “圆的、甜的、带果柄是苹果”。

每个模型都只看自己子集里的水果，独立学习，互不干扰。

4. 新数据：“来了个新水果”

比如仓库里新来了一个水果（红、圆、重 150g、产自山东、甜、带果柄），需要判断它是不是苹果。

5. 模型投票：“5 个评委各说各的”

把这个新水果交给 5 个模型（评委）分别判断：

1. M₁看了说：“红、圆、重 150g，是苹果！”
2. M₂看了说：“红、甜、产自山东，是苹果！”
3. ……
4. M₅看了说：“圆、甜、带果柄，是苹果！”

6. 投票→分类结果：“少数服从多数”

5 个评委都判定是苹果，最终结果就会输出 “这个水果是苹果”。如果有 3 个说 “是”，2 个说 “不是”，也按多数票判定为 “是苹果”。

装袋的核心逻辑（对应图中箭头）：

1. 虚线箭头（D→D₁/D₂…）：表示从原数据集中有放回地抽取子集；
2. 实线箭头（D₁→M₁，D₂→M₂…）：表示用每个子集训练对应的模型；
3. 模型到 “投票” 的箭头：表示每个模型对新数据的判断结果被汇总；
4. “投票” 到 “分类结果” 的箭头：表示最终按多数票决定结果。

装袋：

“多次随机抽数据，每个数据子集训练一个模型，最后所有模型投票，少数服从多数。”

这样做的好处是：单个模型容易 “看走眼”（比如 M₁可能把红西红柿当苹果），但多个模型一起投票，错误会相互抵消，结果更稳定、更准确～