经典排序算法

掉毛学渣

已于 2022-08-12 22:57:32 修改

阅读量298

点赞数

分类专栏： Leecode 文章标签：排序算法算法数据结构

于 2022-07-25 11:37:04 首次发布

本文链接：https://blog.youkuaiyun.com/wh22141334/article/details/125971632

版权

Leecode 专栏收录该内容

29 篇文章

订阅专栏

冒泡排序

冒泡排序是入门级的排序算法，在循环过程中，如果前后两个数不满足题目要求的升序/降序要求，就交换两个数。
交换的时候只需要i,j两个参数，空间复杂度是 $O (1)$ ，**冒泡排序每次循环将最大值/最小值排到最后一位，如果是n个数的话，那么就需要循环n-1次，比较的次数是：
$(n - 1) + (n - 2) + (n - 3) + ... + 2 + 1$
平均时间复杂度为 $O(n^{2})$ 。

冒泡排序有三种写法：

一边比较一边向后两两交换，将最大值/最小值排到最后一位；
经过优化的写法，使用一个变量记录当前轮次的比较是否发生交换，如果没有发生交换就代表已经有序了，不再继续排序；
进一步优化：除了使用变量记录当前轮次是否发生交换外，再使用一个变量记录上次发生交换的位置，下一轮排序时到达上次交换的位置就停止比较。

示例

用一道leetcode题来做下例子（实际提交时用冒泡排序会超出时间限制）。
在这里插入图片描述

第一种写法

class Solution {
public:
    int maximumProduct(vector<int>& nums) {
        //冒泡排序
        //会超出时间限制，
        int n=nums.size();
        
        for(int i=0;i<n-1;i++)
        {
            for(int j=0;j<n-1-i;j++)
            {
                if(nums[j]>nums[j+1])
                  swap(nums[j],nums[j+1]);

            }
        }
  
        //数组元素有正有负
        return max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);

        
    }
};

第二种写法：

class Solution {
public:
    int maximumProduct(vector<int>& nums) {
        //冒泡排序
        //会超出时间限制，
        int n=nums.size();
        bool swapped=true;
        //冒泡的第二种写法
        for(int i=0;i<n-1;i++)
        {   //前一轮回如果没取反的话 代表数组是有序的 直接打破循环
            if(!swapped)
                break;
            swapped=false;//先置为false
            for(int j=0;j<n-1-i;j++)
            {
                if(nums[j]>nums[j+1])
                    {
                        swap(nums[j],nums[j+1]);
                        swapped=true;//当发生了交换才取反
                    }
            }

        }
        //数组元素有正有负
        return max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);
     
    }
};

第三种写法：

class Solution {
public:
    int maximumProduct(vector<int>& nums) {
        //冒泡排序
        //会超出时间限制，
        int n=nums.size();
        bool swapped=true;
        //冒泡的第三种写法
        int lastsortindex=n-1;
        int index=-1;//记录下每次交换的数组元素index
        for(int i=0;i<n-1;i++)
        {
            if(!swapped)
                break;
            swapped=false;
            //到达最后一次交换的index就可以
            for(int j=0;j<lastsortindex;j++)
            {
                if(nums[j]>nums[j+1])
                {
                    swapped=true;
                    index=j;
                    swap(nums[j],nums[j+1]);
                }
            }
            lastsortindex=index;
        }
        return max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);       
    }
};

交换的小技巧

一般我们写交换函数的时候，都采用下面这种代码：

int temp=arr[i];
arr[i]=arr[i+1];
arr[i+1]=temp;

但是如何在**不引入第三方变量的情况下，完成两个数字的交换？**一个数学上的技巧是：

arr[j+1]=arr[j+1]+arr[j];
arr[j]=arr[j+1]-arr[j];
arr[j+1]=arr[j+1]-arr[j];

除了先加后减的方法，还可以先减后加：

arr[j+1]=arr[j]-arr[j+1];
arr[j]=arr[j]-arr[j+1];
arr[j+1]=arr[j+1]+arr[j];

但是这两种方式和容易造成数字越界，最好的方式是通过异或位运算完成数字交换。

arr[j]=arr[j+1]^arr[j];
arr[j+1]=arr[j]^arr[j+1];
arr[j]=arr[j]^arr[j+1];

选择排序

选择排序的算法步骤如下图所示：

先在未排序的数组中找到最大（最小元素）放到数组的首位；
继续在未排完序的数组中找到最小值，放到排完序的数组后面；
继续第二步，直到数组排序完毕
从图中可以看出，每一轮排序都找到了当前的最小值，将其交换至本轮首位。

选择排序与冒泡排序的区别

选择排序和冒泡排序的时空复杂度都是一样的，但是二者的区别在于：冒泡排序在比较的过程中不断交换，而选择排序增加一个变量保存了最小值/最大值的下标，遍历完才交换，减少了交换次数，并且冒泡排序比选择排序稳定。

什么是排序算法的稳定性？

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。
转自：https://leetcode.cn/leetbook/read/sort-algorithms/ev1l5g/

举个例子：
在对数组 $[2, 2, 1]$ 进行排序时，冒泡排序就是稳定的，选择排序就是不稳定的。
当要排序的内容是一个对象的多个属性，且原本的顺序存在意义时，如果要
在二次排序后保持原有排序的意义，就需要稳定的算法。

选择排序的两种写法

每次选择出最小或最大值，放到当前本轮首位
每次选择出最大值和最小值，分别放到当前轮次的首尾。

示例

还是以leetcode题来示例怎么写选择排序，实际提交的时候会超时
在这里插入图片描述

第一种写法：

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {

      //选择排序
        int MaxIndex;
        int n=nums.size();
        for(int i=0;i<k;i++)
        {
          MaxIndex=i;
          for(int j=i+1;j<n;j++)
          {
            //找到最小值
            if(nums[MaxIndex]<nums[j])
            {
              MaxIndex=j;
            }
          }
          //交换到轮次首位
          swap(nums[i],nums[MaxIndex]);
        }
        return nums[k-1];
    }
};

第二种写法

class Solution {
public:
    void twoeleselectionsort(vector<int>& nums)
    {
        int MinIndex,MaxIndex,n=nums.size();
        for(int i=0;i<n/2;i++)
        {
            MaxIndex=i;
            MinIndex=i;
            for(int j=i+1;j<n-i;j++)
            {
                if(nums[MinIndex]>nums[j])
                    MinIndex=j;
                if(nums[MaxIndex]<nums[j])
                    MaxIndex=j;
            }
            //如果MaxIndex=MinIndex，那么说明数组是排序好的
            if(MinIndex==MaxIndex)
                break;
            swap(nums[MinIndex],nums[i]);
            //如果MaxIndex是i的话，因为刚才交换了，所以要重新赋值
            if(MaxIndex==i)
                MaxIndex=MinIndex;
            int lastIndex=n-i-1;
            swap(nums[MaxIndex], nums[lastIndex]);
        }

    }
    vector<int> sortArray(vector<int>& nums) {
        //selectionSort(nums);
        twoeleselectionsort(nums);
        return nums;

    }
};

希尔排序

希尔排序本质上是对插入排序的一种优化，希尔排序的思想是：

将待排序数组按照一定的间隔跳跃取多个子数组，每组分别进行插入排序；
逐渐缩小间隔进行下一轮排序
最后一轮时，间隔为1。

示例：
对数组 $[34, 67, 89, 23, 31, 45, 56, 76, 20, 32]$ 进行希尔排序的过程如下：

第一步：间隔为5划分数组，分为了5组，分别是 $[34, 45], [67, 56], [89, 76], [23, 20], [31, 32]$ ，对他们进行插入排序后为： $[34, 45], [56, 67], [76, 89], [20, 23], [31, 32]$ ，此时整个数组变成了 $[34, 56, 76, 20, 31, 45, 67, 89, 23, 32]$
第二步：间隔2划分数组，分为了2组，分别是 $[34, 76, 31, 67, 23]$ 和 $[56, 20, 45, 89, 32]$ ，进行插入排序后，变成 $[23, 31, 34, 67, 76]$ 和 $[20, 32, 45, 56, 89]$ ，此时整个数组为 $[23, 20, 31, 32, 34, 45, 67, 56, 76, 89]$ 。可以发现：当我们完成2间隔排序后，这个数组仍然是保持5间隔有序的，更小间隔的排序并没破坏上一步的结果。
第三遍：1间隔排序，直接对整个数组进行排序，排序后数组成为 $[20, 23, 31, 32, 34, 45, 56, 67, 76, 89]$ 。

增量序列

希尔排序中每一遍排序的间隔称为增量，所有的增量组成的序列称为增量序列，增量依次递减，减，最后一次增量为1，希尔排序可以分为下面两个步骤

定义增量序列 $D_{m}>D_{m-1}>D_{m-2}>...>D_{1}=1$
对每个 $D_{k}$ 进行间隔排序
增量序列的选择一般可选择为 $D_{m}=N/2,D_{k}=D_{k+1}/2$ ，

示例

在这里插入图片描述

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        for(int gap=nums.size()/2;gap>0;gap/=2)
        {
            for(int gapstartIndex=0;gapstartIndex<gap;gapstartIndex++)
            {
                for(int currentIndex=gapstartIndex;currentIndex<=nums.size()-1;currentIndex+=gap)
                {
                    int currentNum=nums[currentIndex];
                    int preIndex=currentIndex-gap;
                    while(preIndex>=gapstartIndex && currentNum<nums[preIndex])
                    {
                        nums[preIndex+gap]=nums[preIndex];
                        preIndex-=gap;
                        
                    }
                    nums[preIndex+gap]=currentNum;

                }
            }
        }
        return nums;
    }
};

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
      //希尔排序
      int n=nums.size();
      //gap序列
      for(int gap=n/2;gap>0;gap/=2)
      {
        //i从gap开始，到终点结束
          for(int i=gap;i<n;i++)
          {
            int preIndex=i-gap;
            int currentNum=nums[i];
            while(preIndex>=0 && nums[preIndex]>currentNum)
            {
              nums[preIndex+gap]=nums[preIndex];
              preIndex-=gap;
            }
            nums[preIndex+gap]=currentNum;
          }
      }
      return nums;
    }
};

堆排序

什么是堆

堆是符合下列条件之一的完全二叉树，

根节点的值 $\geq$ 子节点的值，这样的堆称为最大堆，或者大顶堆
根节点的值 $\leq$ 子节点的值，这样的堆称为最小堆，或者小顶堆

堆排序过程

用数列构建出一个大顶堆，取出堆顶的数字
调整剩余的数字，再次构建大顶堆，再次取出堆顶的数字
循环往复，完成整个排序

补充知识

对于有N个元素的完全二叉树的，最后一个非叶子下标为 $N /2 - 1$
对于完全二叉树中的第i个数，左子节点下标为： $l e f t = 2 i + 1$
对于完全二叉树中的第i个数，右子节点下标为： $r i g h t = l e f t + 1$

我们以数组 $[4, 6, 8, 5, 9]$ 为例来讲述一下堆排序的过程：
1、先构建大顶堆
在这里插入图片描述
找到第一个非叶子节点6，比较根节点和子节点的值，因为6<9，所以交换，交换后符合大根堆的规律

在这里插入图片描述
找到第二个非叶子节点，由于4的左节点9比4大，右节点也比四大，所以交换

交换后，根节点4不符合大顶堆规律，调整

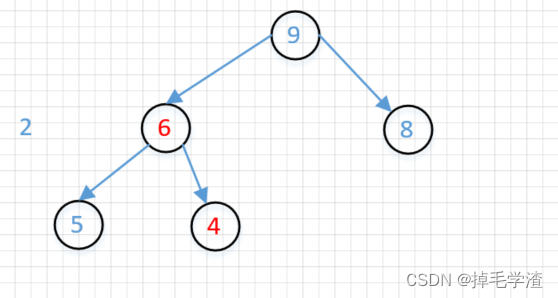
交换后，大顶堆就完整了。
2、交换堆元素
交换堆顶和堆尾元素，获得最大元素
在这里插入图片描述
交换后，需要再次构建大顶堆

再次交换堆尾和堆首，获得第二大元素

然后重复以上过程

直到完成排序。

示例

在这里插入图片描述

class Solution {
public:
    void heapsort(vector<int>&nums,int i,int n)
    {
        //左节点，右节点
        int left=2*i+1,right=left+1;
        //叶子节点
        int largestIndex=i;
        //选择排序
        if(left<n&&nums[largestIndex]<nums[left])
            largestIndex=left;
        if(right<n&&nums[largestIndex]<nums[right])
            largestIndex=right;
        if(largestIndex!=i)
        {
            swap(nums[largestIndex],nums[i]);
            //重新调整改变后的二叉树
            heapsort(nums, largestIndex,n);
        }

    }
    void buildMaxHeap(vector<int>& nums)
    {   //最后一个叶子节点的值
        for(int i=nums.size()/2-1;i>=0;i--)
        {
            heapsort(nums, i, nums.size());
        }
    }
    int findKthLargest(vector<int>& nums, int k) {
        //这时候是大顶堆
        buildMaxHeap(nums);
        //第k个最大的元素，
        for(int i=nums.size()-1;i>nums.size()-k;i--)
        {
            swap(nums[0],nums[i]);
            heapsort(nums, 0, i);
        }
        return nums[0];
        
    }
};

快速排序

思想

从数组中取出一个数，称为基数
遍历整个数组，比基数大的放到基数右边，比基数小的放到基数左边，遍历完成后，数组以基数为边界，分成了左右两个边界，左边全是比基数小的，右边全是比基数大的。
再对左右两个边界进行排序，直到排序完成。

示例

在这里插入图片描述 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-geo6T8MY-1660314591274)(https://img-blog.csdnig.cn/c50efc9f53bf4186bdd11d90af964924.png)]

代码

int parttion(vector<int>&nums, int start, int end)
{
    int pviot = nums[start];
    int left = start+1, right = end;
    while (left < right)
    {
        //找到第一个比基准值大的
       while (left<right && nums[left]<=pviot)
            left++;
       //找到第一个比基准值小的
       while (left < right && nums[right] > pviot)
            right--;  
       //交换两值
       if (left < right)
       {
           swap(nums[left], nums[right]);
           left++;
           right--;
       }
    }
    if (left == right && nums[right] > pviot)
        right--;
    if (right != start)
        swap(nums[right], nums[start]);
    return right;    //返回分界
}
void quickSort(vector<int>& nums, int start, int end)
{
    if (start >= end)
        return ;
    int middle = parttion(nums, start, end);
    quickSort(nums, start, middle -1);
    quickSort(nums, middle + 1, end);
}

排序算法–归并排序

思想：
归并排序采用经典的分治法将问题分割成一些小的问题，然后递归求解。
图解：
在这里插入图片描述

示例

在这里插入图片描述

class Solution {
public:
    void sortmerge(vector<int>& nums,int left, int right)
    {
        int center;//求出分割字符串的中心
        if(left<right)
        {
          center=(left+right)/2;
          sortmerge(nums,left,center);//分割排序左字符串
          sortmerge(nums,center+1,right);//分割排序右字符串
          merge(nums,left,center,right);//合并
        }
    }
    void merge(vector<int>& nums,int left,int center,int right)
    {
      vector<int> temps(right-left+1);
      int rightstart=center+1;
      int tempstart=0,j=0;
      int temp=left;
      while(left<=center && rightstart<=right)
      {
        if(nums[left]<=nums[rightstart])
          temps[tempstart++]=nums[left++];
        else
          temps[tempstart++]=nums[rightstart++];
      }
      while(left<=center)
        temps[tempstart++]=nums[left++];
      while(rightstart<=right)
        temps[tempstart++]=nums[rightstart++];
      while(temp<=right)
        nums[temp++]=temps[j++];
      
    }
    vector<int> sortArray(vector<int>& nums) {
      //归并排序
      int right=nums.size()-1;
      int left=0;
      sortmerge(nums,left,right);
      return nums;
    }
};