#734. 徐老师的养花装置

 

因为每次进行操作，都是对连续的一段后缀进行操作的，而同时进行操作的数字之间相对差值

不会发生变化。

所以很容易想到，操作第一个数字没有意义，所以一定是让后面 个数字变成第 个数

字

那么不考虑可以修改一个数字的话，答案其实就是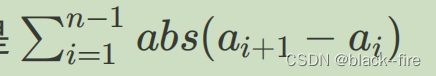

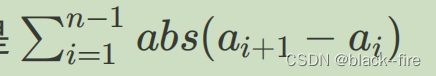
 接着考虑修改一个数字能够造成的效果，修改的数字必然是让一个数字变成它两边的数字，可以使得少去一个数字需要操作 。例如将a[i+1] 变成a[i] ，这样修改以后原本的 abs(a[i+1] − a[i]) + abs(a[i+2] − a[i+1]) 的操作次数就变成了abs(a[i+2] − a[i])，所以能够节省的abs(a[i+2] − a[i])操作次数就是abs(a[i+1] − a[i]) + abs(a[i+2] − a[i+1]) − abs(a[i+2] − a[i])，那么我们只要求出最大能节省的操作次数，然后从总 和里减去即可。

代码:

#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll shen,a[200009],n;
ll f()
{
  ll ans = 0;
  for(ll i = 2; i <= n; i++) ans += abs(a[i] - a[i - 1]);
  return ans; 
}
int main()
{
  cin>>n;
  for(ll i = 1; i <= n; i++) cin>>a[i];
  for(ll i = 1; i <= n; i++)
  {
    if(i == 1) 	shen = max(shen,abs(a[2] - a[1]));
    else if(i == n) shen = max(shen,abs(a[n] - a[n - 1]));
    else shen = max(abs(a[i] - a[i - 1]) + abs(a[i + 1] - a[i]) - abs(a[i + 1] - a[i - 1]),shen);
  }
  cout<<f() - shen;
  return 0;
}