[算法导论]归并排序

时间复杂度

《算法导论》2.3.1 分治法。

归并排序采用了分治法的递归排序。分治法：分解子问题，解决子问题，合并子结果。

分解：分解待排序的 $n$ 个元素的序列各成 $\frac{n}{2}$ 个元素的子列。

解决：使用归并排序递å归地排序两个子序列。

合并：合并两个已排序的子序列以产生已排序的答案。

因为排序数组会被 $\frac{n}{2}$ 拆开，归并排序时间复杂度稳定的 $nlgn$。

相对于其它的 $nlgn$ 排序，它需要额外的临时空间辅助，有一定的资源损耗。小数量级（百万级别）的排序，要比快速排序慢。但是大数量级数据（千万级别），因为归并排序树深最小，排序比快速排序快。

快速排序，最优算法复杂度，数组会被 $\frac{n}{2}$ 拆开。实际操作中数据很难达到最优。而归并一直都是通过 $\frac{n}{2}$ 进行拆分。

---

算法

算法导论实现思想

1. 拆分左右两个临时数组，临时数组最后是一个∞无穷大的数字。
2. 两个子数组进行比较，小的数值会拷贝到原数组。

---

实现

实际实现，通过一个辅助数组进行实现(源码)。

void merge_sort(int array[], int start, int mid, int end) {
    int k = 0;
    int low = start;
    int high = mid + 1;
    int* temp = (int*)malloc(sizeof(int) * (end - start + 1));
    
    while (low <= mid && high <= end) {
        (array[low] < array[high]) ? temp[k++] = array[low++]
                                   : temp[k++] = array[high++];
    }

    while (high <= end) temp[k++] = array[high++];
    while (low <= mid) temp[k++] = array[low++];
    for (int i = 0; i < k; i++) array[start + i] = temp[i];

    free(temp);
}

void merge(int array[], int start, int end) {
    if (start >= end) {
        return;
    }

    int mid = (start + end) / 2;
    merge(array, start, mid);
    merge(array, mid + 1, end);
    merge_sort(array, start, mid, end);
}

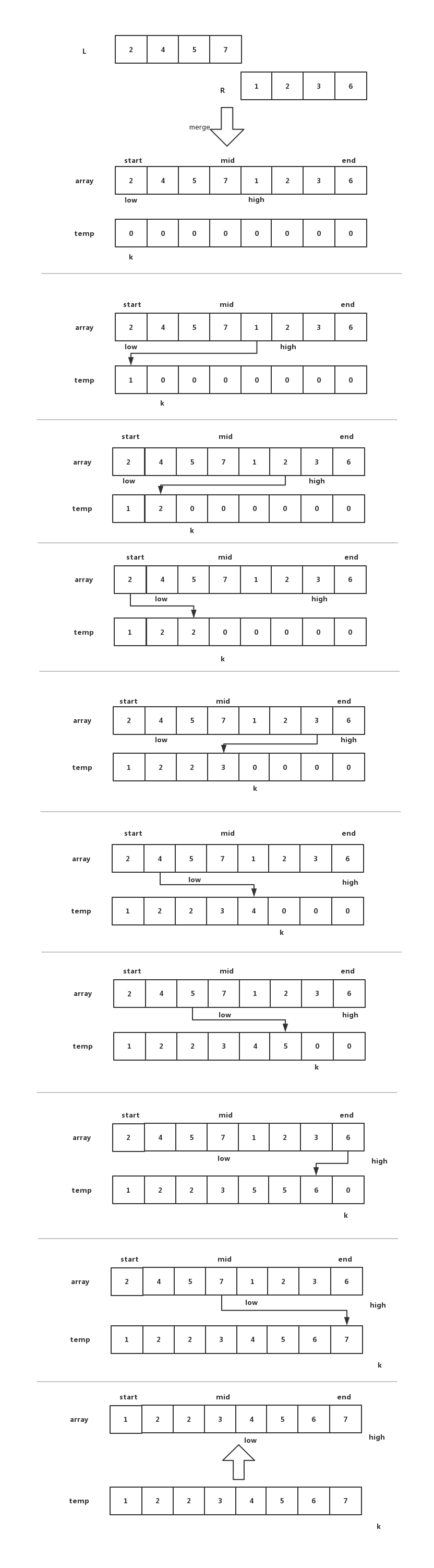
实现流程

数组 A = {5, 2,4,7, 1, 3, 2, 6} 子数组最后一次合并排序流程。

---

参考

快速排序、归并排序、堆排序三种算法性能比较