CFF_201812-4——数据中心（最小生成树kruskal&并查集）

最新推荐文章于 2020-04-03 00:21:34 发布

北极星以南南

最新推荐文章于 2020-04-03 00:21:34 发布

阅读量247

点赞数

CC 4.0 BY-SA版权

分类专栏： CCF 文章标签：最小生成树并查集

本文链接：https://blog.youkuaiyun.com/wen_zihan/article/details/88608433

CCF 专栏收录该内容

12 篇文章

订阅专栏

本文深入探讨了Kruskal算法在解决最小生成树问题中的应用，详细讲解了算法的实现过程，包括初始化、查找并集操作以及如何避免形成环路等关键步骤。通过具体代码示例，展示了如何使用Kruskal算法找到加权图中最大边长，适用于边较少的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

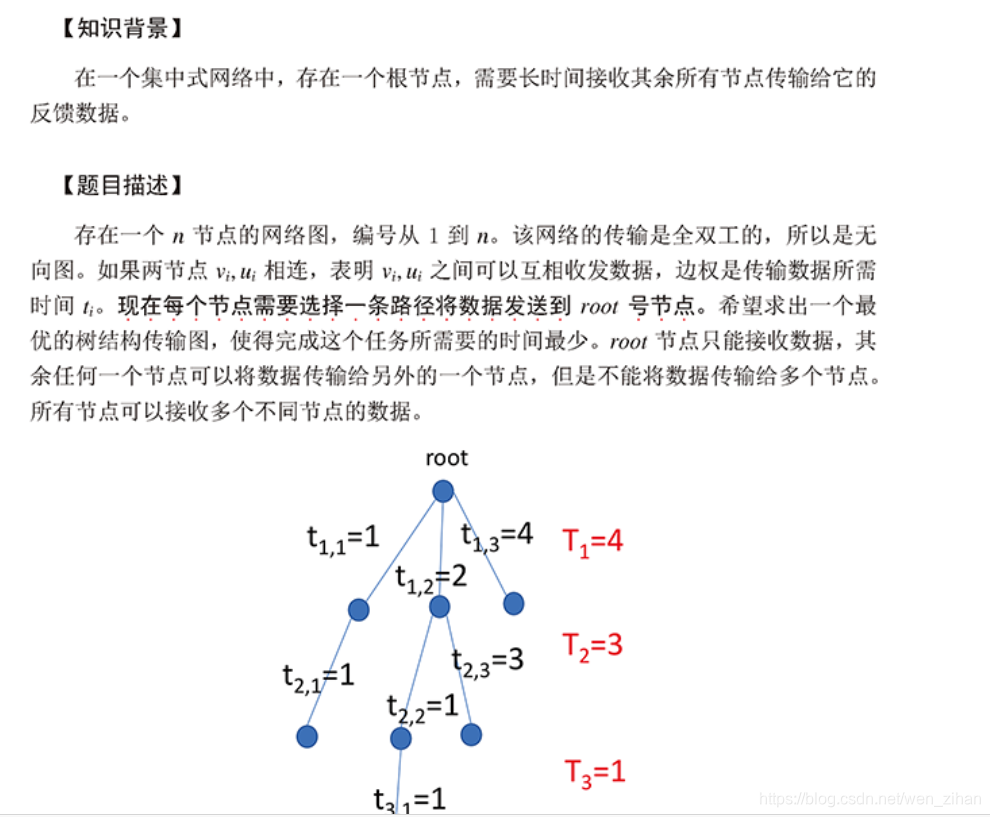
4
5
1
1 2 3
1 3 4
1 4 5
2 3 8
3 4 2

样例输出

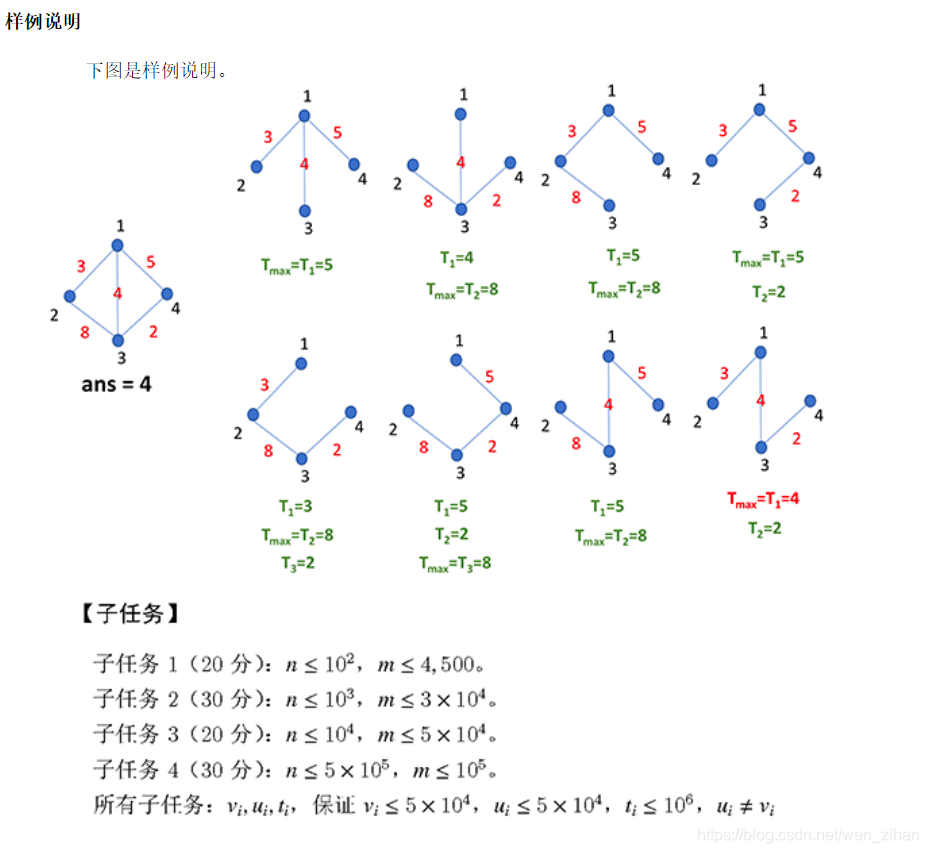
1.最小生成树问题，求最大边长，与root无关

2.prim算法适合边比较少的（最优灌溉），比较好遍历，这里用prim会超时

3.用kruskal算法，在find函数里不进行路径压缩也会超时

#include<stdio.h>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int father[500005];
int n,m,root;
int v,u;
long long t;
struct Edge
{
	int from;
	int to;
	long long t;
}edge[100005];

int cmp(const void *a,const void *b)
{
	return((struct Edge*)a)->t-((struct Edge*)b)->t;
}
void init()
{
	for(int i=0;i<=n;i++)
	father[i]=i;
}
int find(int x)
{
	int r=x;
	if(x==father[x])
	  return x;
	  while(x!=father[x])
	   x=father[x];
	   father[r]=x;
	  return x;
}
bool unio(int x,int y)
{
	int px=find(x);
	int py=find(y);
	if(px!=py)
	{
		father[px]=py;
		return true;
	}
	else
	return false;
}
int main()
{
   long long ans_time=-1;
   cin>>n>>m>>root;
   init();
   for(int i=0;i<m;i++)
   {
	 cin>>v>>u>>t;
	 edge[i].from=v;
	 edge[i].to=u;
	 edge[i].t=t;
   }
   qsort(edge,m,sizeof(struct Edge),cmp);
   
   int queue_num=0;
   for(int i=0;i<m;i++)
   {
	  if(unio(edge[i].from,edge[i].to))//不构成环
	  {
	  	queue_num++;
	  	ans_time=edge[i].t;
	  	if(queue_num==n-1)
		  break;
	  }
   }
   cout<<ans_time<<endl;
   return 0;
}