The Max Trick when Computing Softmax

The softmax function appears in many machine learning algorithms. The idea is, if you have a set of values, to scale them so they sum to 1.0 and therefore can be interpreted as probabilities.

For example, suppose you have three values, (x0, x1, x2) = (3.0, 5.0, 2.0). The softmax function for any value xj expressed mathematically is:

SoftmaxEquation

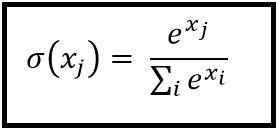
In words, find the sum of e raised to each x value. The softmax for a particular x is e raised to x divided by the sum. So:

exp(3.0) = 20.0855
exp(5.0) = 148.4132
exp(2.0) = 7.3891
sum      = 175.8878

And the softmax values are:

s(3.0) = 20.0855 / 175.8878  = 0.12
s(5.0) = 148.4132 / 175.8878 = 0.84
s(2.0) = 7.3891 / 175.8878   = 0.04

Notice the softmax values sum to 1.0. In practice, calculating softmax values can go wrong if an x value is very large — the exp() of a large number can be huge, which makes the sum huge, and dividing by a huge number can cause arithmetic computation problems.

A trick to avoid this computation problem is subtract the largest x value from each x value. It turns out that the properties of the exp() function give you the same resuilt but you avoid large numbers.

For (3.0, 5.0, 2.0), the largest value is 5.0. Subtracting 5.0 from each gives (-2.0 0.0, -3.0), and so:

exp(-2.0) = 0.1353
exp(0.0)  = 1.0000
exp(-3.0) = 0.0498
sum       = 1.1852

And then:

s(3.0) = 0.1353 / 1.1852 = 0.12
s(5.0) = 1.0000 / 1.1852 = 0.84
s(2.0) = 0.0498 / 1.1852 = 0.04

which are the same softmax values as when computed directly.