AES算法加密

1. 前言

学习视频：【AES加密算法】| AES加密过程详解| 对称加密| Rijndael-128| 密码学| 信息安全_哔哩哔哩_bilibili

相关文档：https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197-upd1.pdf

https://bbs.kanxue.com/thread-253884.htm

2. 基本概念

AES属于分组加密算法，明文长度固定为128位，密钥长度可以是128、192、256位，那么相应地轮数为10、12、14

2.1 设计要求

1. 安全性：可以抵抗目前所有已知攻击，代表了当今商业密码的最高水平
2. 实用性：适应各种应用环境，加解密速度快
3. 扩展性：分组长度和密钥长度可扩展，可以适应社会对保密性不断提高的需求

2.2 整体特点

1. 分组密码：明文和密文长度128，密钥长度可变（128/192/256等）
2. 面向二进制的密码算法
3. 不是对合运算：加解密使用不同的算法
4. 综合运用多种密码技术
5. 整体结构：SP结构

2.3 应用

1. 许多国际组织采用为标准
2. 产品形式：各种软硬件形式
3. 应用范围逐渐扩大

3. 加密流程

最终轮处具体进行字节代换、行移位、轮密钥加，不进行列混合操作

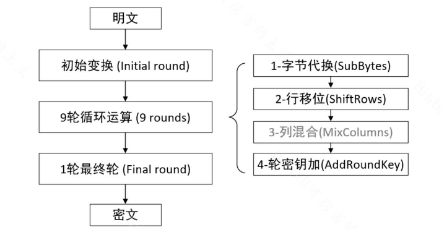
3.1 明文处理

AES 将每个块视为按列主序排列的 16 字节（4 字节 x 4 字节 = 128）网格。

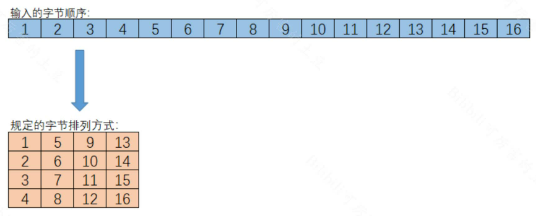
3.2 初始变换

初始变换（Initial round）：将输入的明文与子密钥进行异或

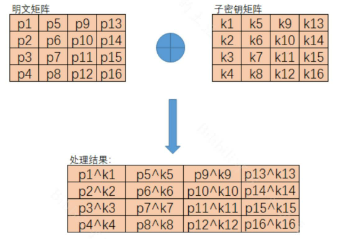
3.3 循环运算

3.3.1 字节代换

根据S盒进行替换，S盒是16×16个字节组成的矩阵，行列的索引值分别从0开始，到十六进制的F结束，每个字节的范围为（00-FF）。

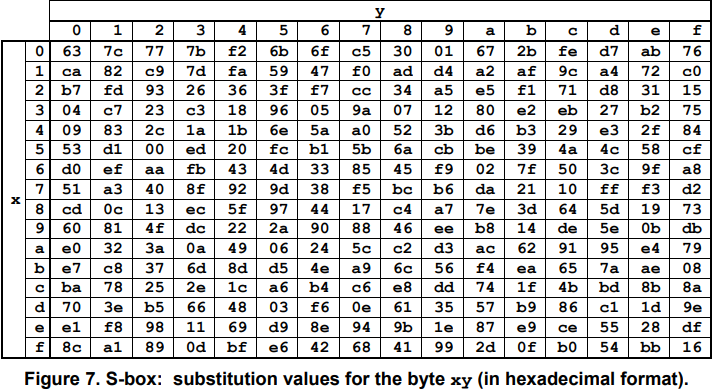
3.3.2 行移位

第一行保持不变，第二行循环左移8比特，第三行循环左移16比特，第四行循环左移24比特。

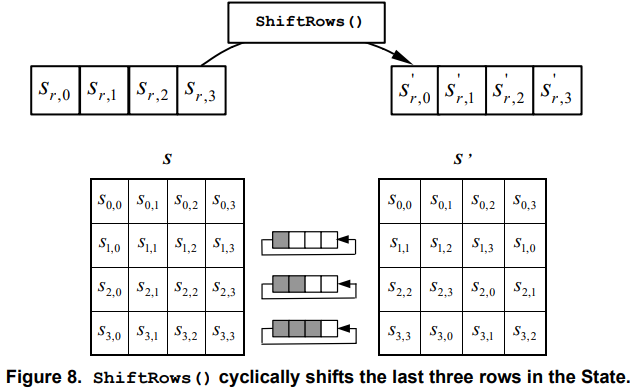
3.3.3 列混合

将输入的的矩阵左乘一个给定$4\ast 4$ 的矩阵

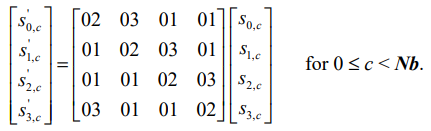
具体的计算方法：

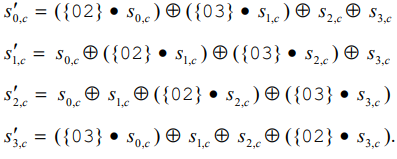
进行乘法运算时，有以下规则：

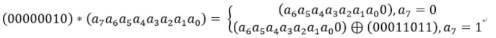
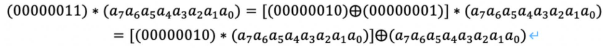
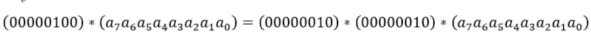
3.3.4 轮密钥加

将结果与轮密钥矩阵进行异或

4. 密钥扩展

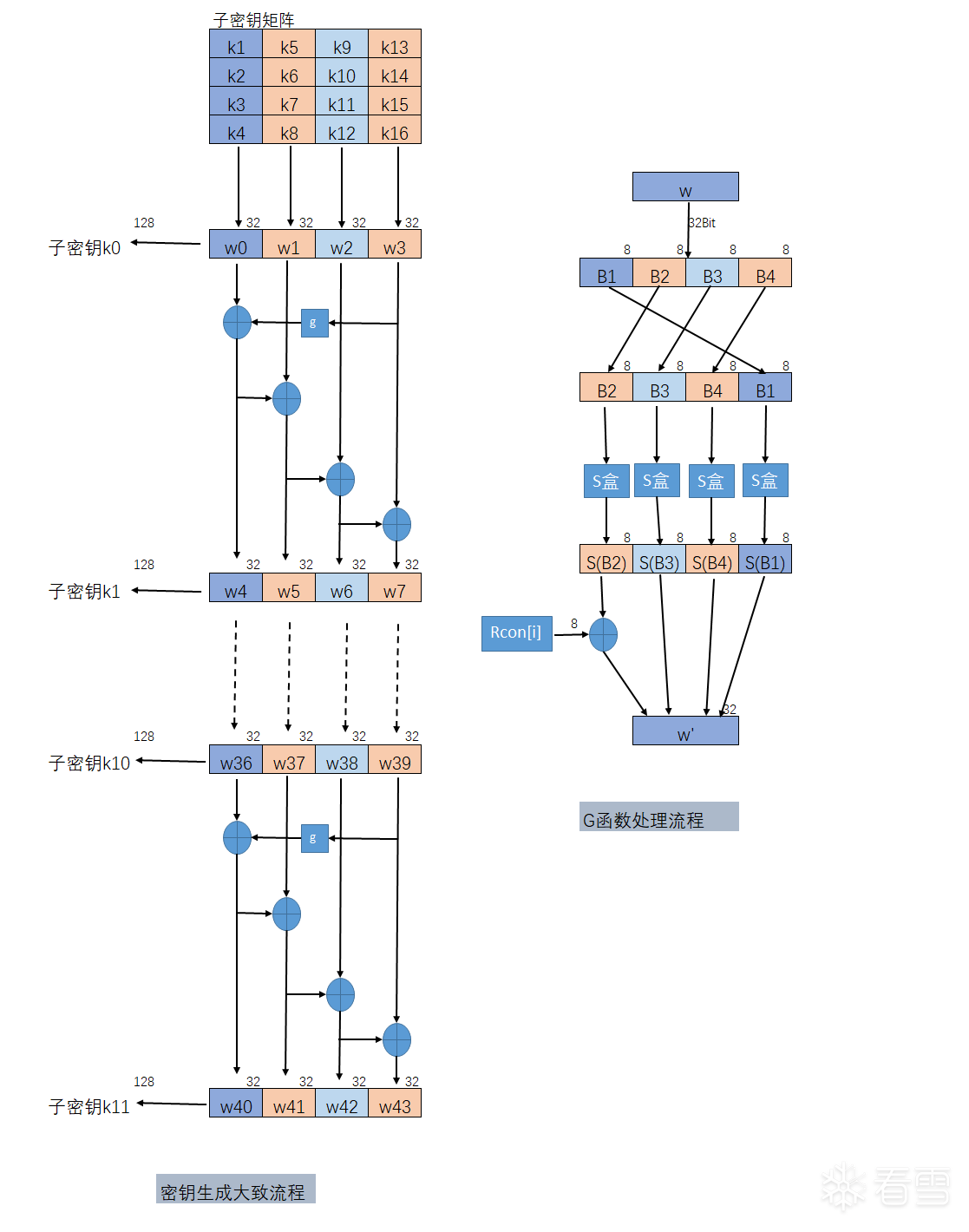
4.1 轮密钥生成

子密钥的生成是以列为单位进行的，一列是32Bit，四列组成子密钥共128Bit。生成子密钥的数量比AES算法的轮数多一个，因为第一个密钥加法层进行密钥漂白时也需要子密钥。

1. 如果$i$不是$4$的倍数，那么第$i$列由如下等式确定：$W[i]=W[i-4]\oplus W[i-1]$
2. 如果$i$是$4$的倍数，那么第$i$列由如下等式确定：$W[i]=W[i-4]\oplus T(W[i-1])$
   

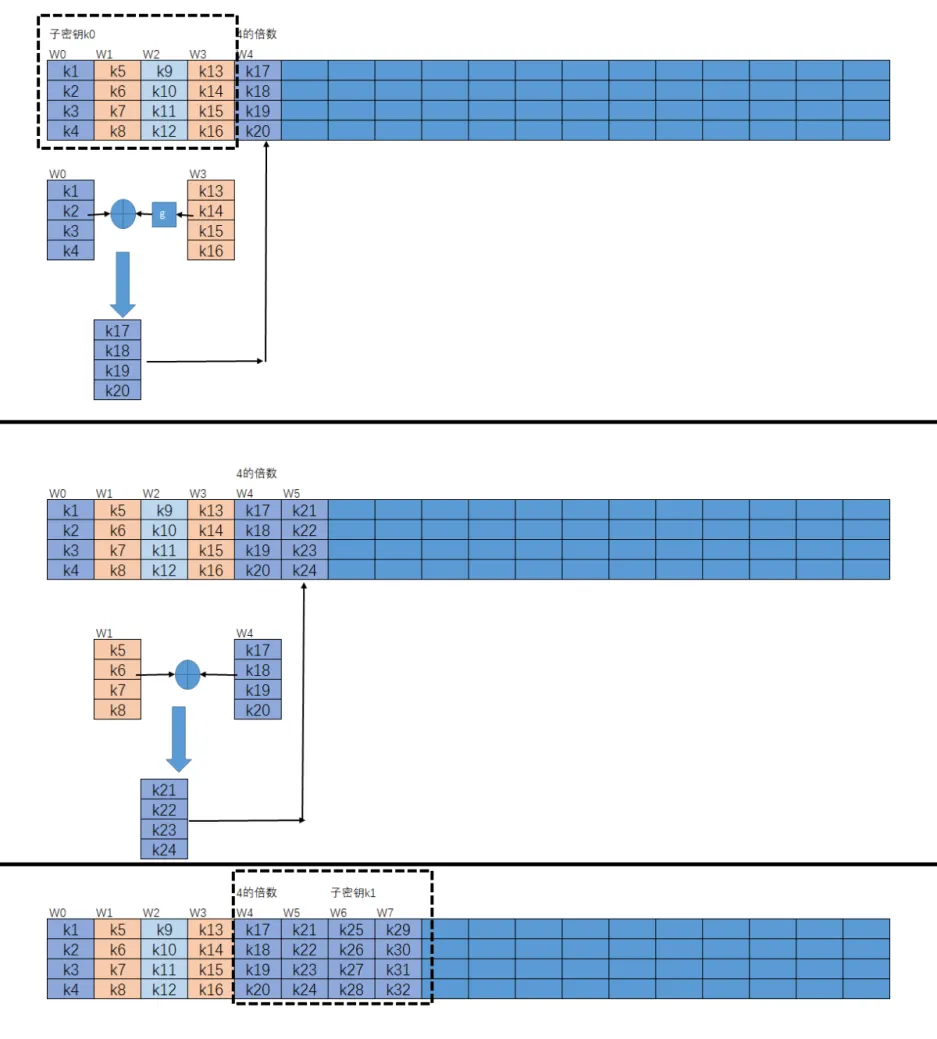
4.2 T函数

4.2.1 字循环

将$1$个字中的$4$个字节循环左移$1$个字节，即将输入字$[b0,b1,b2,b3]$变换成$[b1,b2,b3,b4]$

4.2.2 字节代换

对字循环的结果使用S盒进行字节代换

4.2.2 轮常量异或

将前两步的结果同轮常量$Rcon[j]$进行异或，其中$j$表示轮数