(java)排序算法的全部解析和代码

 时间复杂度的解析点这

排序算法功能都一样只是运行时间有差异，使用上来说只用学一两个就行了

1.最好写且性能不错的，推荐看完插入排序用Arrays.sort(数组，comparator匿名内部类重写compare方法）

2.速度很快且不占用内存，推荐快速排序

3.不在乎好不写和内存占用过高炸堆，64g内存条无所畏惧只要求极致速度，推荐基数排序

 外部排序是指内存和硬盘混用来进行排序的算法，本篇文章不包括外部排序

1.冒泡排序:两层循环第一层从右往左缩减区间，第二层从左往右把当前区间最大值带到右边界上

红色是第一层循环，绿色是第二层

public class bubble {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] a = {9,3,-1,3,7};
		int temp = 0;
		boolean flag = false;

		for (int i = 0; i < a.length-1; i++) {
			for (int j = 0; j < a.length-1-i; j++) {
				if(a[j] > a[j+1]) {//如果右边小于左边的
					flag = true;//在从右向左不断缩减的区间里有排序不合理的地方，
					temp = a[j+1];//右边拿手上
					a[j+1] = a[j];//左边放右边
					a[j] = temp;//手上放左边
					//j循环相当于把0-length-1-i这个区间里最大的数带到区间最右边
				}
			}
			//如果当前从左向右区间遍历后没有排序不合理的数就进行break
			if(!flag) {
				break;
			}else {
				flag = false;
			}
		}
		
		for (int i = 0; i < a.length; i++) {
			System.out.print(a[i] + " ");
		}

	}

}

2.选择排序（刚好和冒泡是反过来的）

从左往右缩减遍历区间，每次从遍历区间选个最小的和 左边界交换位置

public class choice {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] a = {2,3,32,6,7,335,4,-8};
		int min = 0;
		int minindex = 0;
		
		for (int i = 0; i < a.length-1; i++) {
			minindex = i;
			min = a[i];
			for (int j = i+1; j < a.length; j++) {
				if(a[j]< min ) {
					min = a[j];//最小的数
					minindex = j;//最小数的索引
				}
			}
			if(minindex != 0) {//minindex=0说明当前区间所有数都是正确排列的，因此没必要交换
				a[minindex] = a[i];
				a[i] = min;
			}
			
		}
		for (int i = 0; i < a.length; i++) {
			System.out.print(a[i] +" ");
		}

	}

}

 3.插入排序，

类似与给一个乱序文件柜的文件排序，

1.从前往后找到第一个错位的文件把要排序文件拿在手里，此时错位位置是空的，错位位置之前的都是排序好的文件

2.从错位文件位置往前挨个与排序好的文件比对顺序，（顺序取决于你是升序还是降序）

假设是小的在前，大的在后，比错位文件大就往后拨一位，空出大的文件位置，看下一个文件，直到找到比错位文件小的，就在他之后的位置放下错位文件

再把这个文件柜想象成数组就是插入排序了

外层循环是从前往后找到第一个错位文件

内层循环是从错位位置往前摆放错位文件

Arrays类有个sort方法的重写形式就是插入排序

 其中T[]是泛型表示方法运用的数组必须是Integer包装类数组,，comparator是定义比对规则的一个匿名内部类

其中只有这一个方法，可以直接用lambda简写

这个自定义排序规则的sort方法底层是使用二分查找+插入排序

开始的默认0索引的数据是有序序列，然后遍历数组后面的每一个元素，将每一个元素插入到前面有序序列的指定地方。

参数的o1就是错位文件，o2就是与他比较的已排序文件，

返回负数表示o1比o2更靠近索引0

返回正数表示o1比o2更靠近数组.length-1

返回0表示相同

降序简写return o2-o1,升序o1-o2,

由于sort里的数组类型要求是泛型，但其实二维的int数组也是可以用的，不一定要用Integer

写法如下，因为二维数组的每一格也是一个地址型数据，相当于对二维数组里的一维数组进行排序

 

public class insert {

	public static void main(String[] args) {
		SimpleDateFormat si = new SimpleDateFormat("时间ss");
		Random r = new Random();
		
		// TODO Auto-generated method stub
		int[] a = new int[8000];
		for (int i = 0; i < a.length; i++) {
			a[i] = r.nextInt(80000);
		}
		long b =System.currentTimeMillis();
		
		int v = 0;
		int vindex = 0;
		
		for (int i = 0; i < a.length; i++) {
			v = a[i];
			vindex = i-1;
			while(vindex>=0 && a[vindex]> v) {
				a[vindex +1] =  a[vindex];
				vindex--;
			}
			//while完vindex指向的是第一个小于他的值
			if(vindex+1!=i) {
				a[vindex+1] = v;
			}
		}
		long b2 =System.currentTimeMillis();
		System.out.println(b2-b);//排序所需时间（毫秒
		
		long bz =System.currentTimeMillis();
		System.out.println(Arrays.toString(a));
		long b2z =System.currentTimeMillis();
		System.out.println(b2z-bz);//打印被排序后数组的所需时间（毫秒

	}

}

4.希尔排序（插入排序plus)

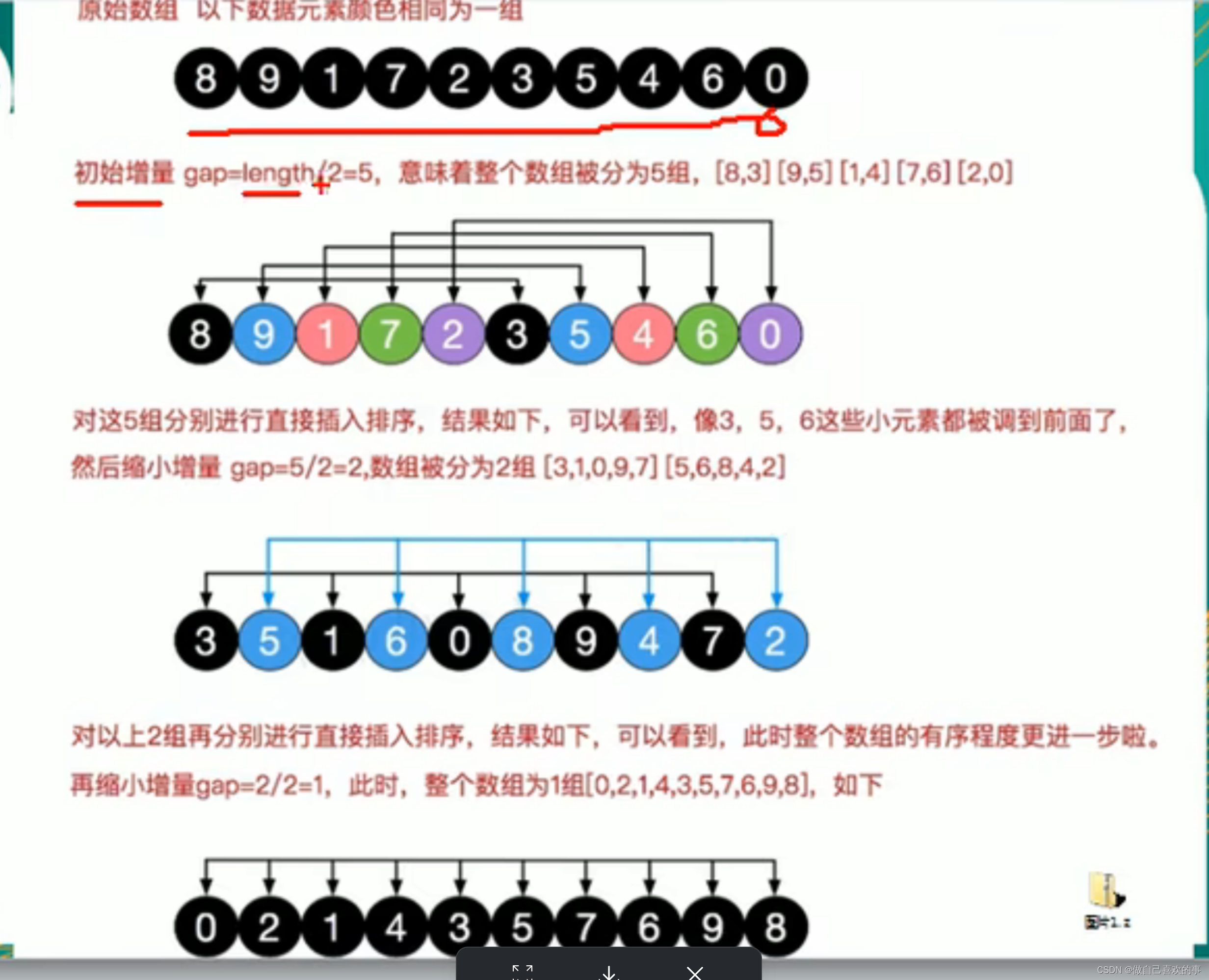
 外层循环i(gap) = length /2  i<length i/=2
内层从i循环到<length
最内层i当作错位文件，往前隔gap个形成的文件数列中进行插入排序
算法可视化网站：Brute Force - Shellsort (algorithm-visualizer.org)

i为3，gap为3时
进行插入排序的数列是0,3
i为6时，数列时0,3,6
这个进行基数排序的各个组不是一开始就全在集合里
而是隔gap-1个每次往右填一位(i+gap)
每填一位对这个数列进行一次基数排序就是把新添加的数在之前排序好的数列里面找位置放下

而且他不是先排好一个组别（集合）
而是从左到右顺着到那个组别就排序那个组
如：gap为3
0，3
1，4
2，5
0，3，6
1，4，7
2，5，8
0，3，6，9
这样的顺序排序数列（这里的数是索引）其中可以发现每个数列最右边的这个索引是从gap循环到length-1为止，同时每循环一次以最右索引i往前找gap个形成要排序的数列，并把当前索引i的这个数当作错位文件，往前隔gap个进行插入排序，由于基数排序本质就是在排序数组里找到错位文件的为止并放下
不论你不停把比错位大的往后拨gap个，找到小的以后再放下错位文件
还是遇到比错位大的就和错位互相交换位置
这两种做法都一样，都是为了在已经排序的数列里面找到错位文件的位置并放下

	
	//交换式希尔排序
	public static void shellchange(int[] arr) {
		int temp = 0;
		for (int gap = arr.length/2; gap > 0; gap/=2) {
			for (int i = gap; i < arr.length; i++) {
				//5,0,,6,1,,7,2,,
				//上面是i,下面相当于while
				//这里用的是直接交换不是插入
				for (int j = i-gap; j >= 0; j-=gap) {
					if(arr[j] > arr[j + gap]) {
						temp = arr[j];
						arr[j] = arr[j+gap];
						arr[j+gap] = temp;
					}
				}
				
			}
		}
	}
	
	//插入式希尔排序
	public static void shellmove(int[] arr) {
		
		
		for (int gap = arr.length/2; gap > 0; gap/=2) {
			for (int i = gap; i < arr.length; i++) {
				int j = i;
				int temp = arr[j];
				if(arr[j] < arr[j -gap]) {
					while(j - gap>=0 && temp < arr[j - gap]) {
						arr[j] = arr [j-gap];
						j -= gap;
					}
					arr[j] = temp;
				}
				
			}
		}
	}

5.快速排序（这个排序用的是递归，数组要是长度过大可能会爆栈，但是速度肯定快）

8千万长度的随机生成的数组排序只要7秒，数组长度要是超过1亿可能就有点慢了

 快排方法本身是对a数组的[L,R]区间进行排序，其中用(L+R)/2当作mid值，比mid小的放左边，大放右边，向内收缩L和R的区间，L和R同时找到错位的数字让这两个数字交换位置，排序完后L=R=mid值索引

再对[0,mid-1] 和[mid+1,length-1]这两个区间分别进行递归排序，区间递归的前提是

mid-1大于0 

mid+1小于length-1

如图递归下去就能排序完了，缺点就是要是数组长度过于长时，还没到达递归最底部进行返回，内存就先受不了了，所以用递归的排序算法基本都有这个缺点

package sort;

import java.util.Arrays;
import java.util.Random;

public class quick {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		//int[] a = {-9,78,0,23,-567,-10,23,23};
		Random r = new Random();
		int[] a = new int[80000000];
		for (int i = 0; i < a.length; i++) {
			a[i] = r.nextInt();
		}
		long b = System.currentTimeMillis();
		quick(a,0,a.length-1);
		
		long z = System.currentTimeMillis();
		
		System.out.println((z-b)/1000);


		//System.out.println(Arrays.toString(a));

	}
	
	public static void quick(int[] arr , int left,int right) {
		int l = left;
		int r = right;
		int mid = arr[(left +right ) /2];
		int temp = 0;
		//中
		//循环的目的是让小的放mid坐边，大的放mid右边
		
		while(l < r ) {
			
			while(arr[l] < mid) {
				//在mid左边一直找大于他的值
				l+=1;
				//左往中间是加
			}
			
			while(arr[r] > mid) {
				//在mid左边一直找大于他的值
				//右往中间是减
				r-=1;
			}
			//上面两个while执行完后l和r指向的都是在左边大于他的值和在右边小于他的值
			//这里移动完有可能l>r,也就是交错了，l=r是两个都是指向mid
			if(l>=r) {//这里改成==也是能运行的，因为这个whilel<r结束时l必定等于r,
				break;
				//左大于右说明左边已经全部是小于等于，右边是大于等于
			}
			
			temp = arr[l];
			arr[l] = arr[r];
			arr[r] = temp;
			//左边比他小才会略过，右边比他大才会略过
			//不满足这两个条件的都会被看作需要交换的值
			//如果交换完后，发现这个arr[1] == mid值 --,前移

			//mid只是个值不是索引
			//假设左右各有两个一样的mid值,他们两个之间会不停的重复交换陷入死循环，因为mid不论在右边还是左边
			//既不大于也不小于他自己所以l和r就卡住了陷入死循环mid不停与另一个mid交换，且由于上一步才进行过一次交换，一边为mid时，另一边只可能有两种情况
			//1.正确位置的数字，反正都位置正确了，略过也无所谓
			//2.同是mid,这种就必须要手动略过
			if(arr[l] == mid) {
				r -= 1;
			}
			
			
			if(arr[r] == mid) {
				l+=1;
			}
		}
		//System.out.println(l+" " + r);
		//执行完while以后l和r其实就等于mid
		//由于循环做了个l==r的break语句，且l和r等于自己的时候也算是执行数
		//判断完中间值的两边后，中间值是不需要再判断的，所以把

		//由于上面循环虽然是l<r,不包括l=r,但lr移动完中间有if(l>=r)强制break
		//且就算移动两边都无法略过mid，因此循环终止时l必定等于r
		//由于mid排序完了要对，[0,mid-1] 和[mid+1,length-1]这两个区间分别进行递归排序
		//由于这时l=r=mid索引，l和r错开一下就是mid+1和mid-1

		if(l == r ) {
			l+=1;
			r-=1;
		}
		//去除中间值后要保证，中间值往左或者往右不能超过原来的边界，就
		
		//参数Left小于变化后的r
		if(left < r ) {
			quick(arr,left,r);
		}
		//参数right 大于变化后的l
		
		if(right> l) {
			quick(arr,l , right);
		}
		
		
		
	}

}

 未完待续。。。。