11-15将有序数组转换为二叉搜索树 验证二叉搜索树

11-15.1 P106将有序数组转换为二叉搜索树

题目描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵

平衡二叉搜索树。

示例 1：

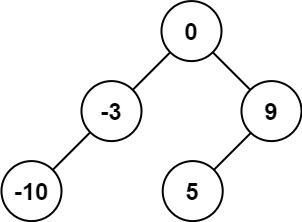
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

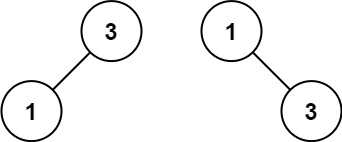
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

题解

首先明白什么是平衡二叉搜索树：排列树+平衡树

排列树：每一个结点：其左子树所有结点<根节点<右子树所有结点

平衡树：每一个结点的左右子树高度差的绝对值不超过1

因为数组元素即结点已经排序，所以只要分出平衡树并确保左子树所有结点<根节点<右子树所有结点

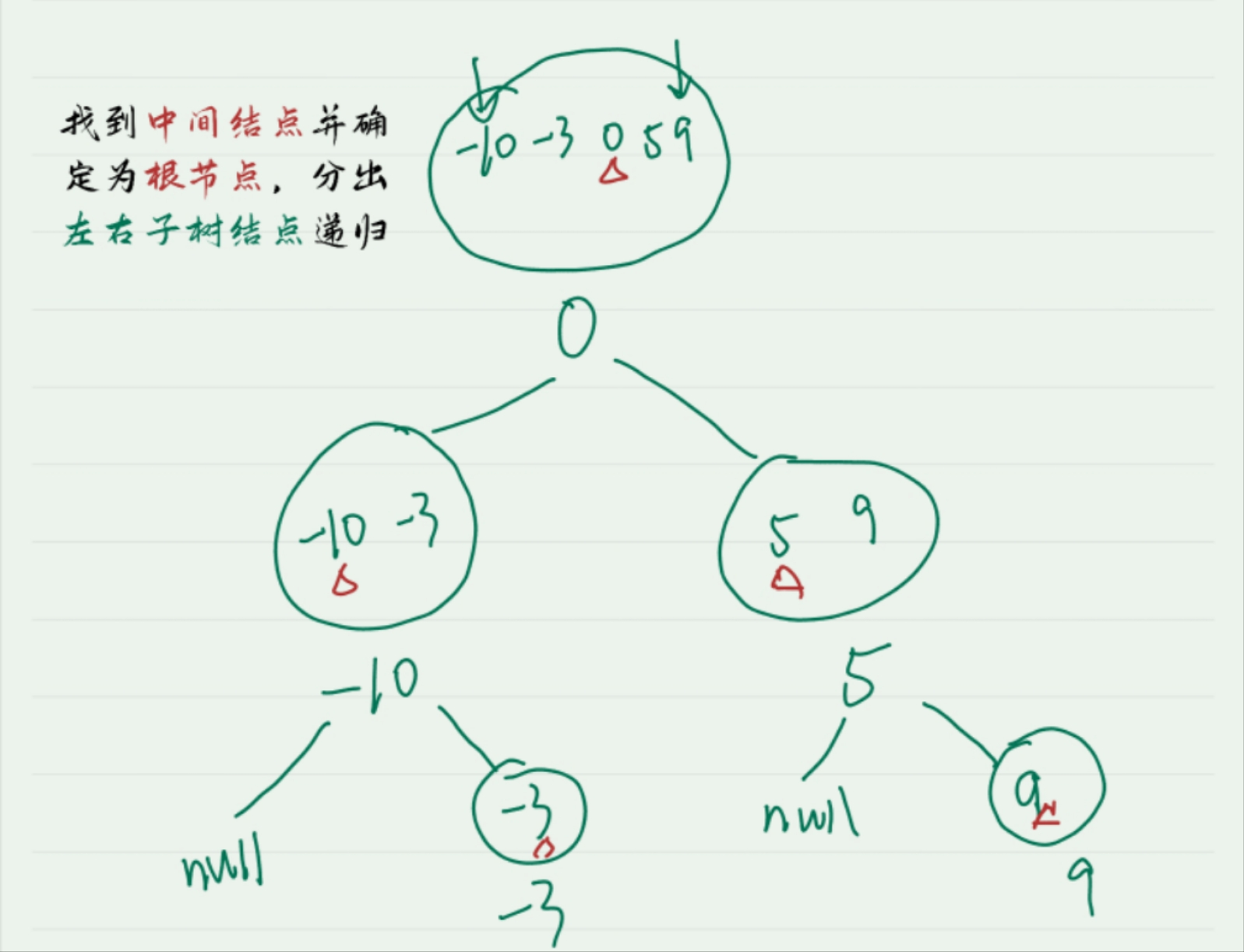
代码

var sortedArrayToBST = function(nums){
    return dsf(nums,0,nums.length-1)
}
function dsf(nums,left,right){
    if(left>right){
        return null
    }
    const m = Math.floor((left+right)/2)
    return new TreeNode(nums[m],dsf(nums,0,m-1),dsf(nums,m+1,nums.length-1))
}

109. 有序链表转换二叉搜索树

给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为 平衡 二叉搜索树。

var sortedListToBST = function(head) {
    if(!head){
        return null
    }
    let slow = head
    let fast = head
    let pre = null
    while(fast&&fast.next){
        pre = slow
        slow = slow.next
        fast = fast.next.next
    }
    let root = new TreeNode(slow.val)
    if(pre){
        pre.next = null
        root.left = sortedListToBST(head)
    }
    root.right=sortedListToBST(slow.next)
    return root
}

11-15.2 P98 验证二叉搜索树

题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左

  子树

  只包含

  小于

  当前节点的数。

• 节点的右子树只包含 大于 当前节点的数。

• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

题解

这题要注意的是每一个结点左子树所有结点<root.val<右子树所有结点。可以看作一个数轴，每一个中间结点必须在（left,right）之内

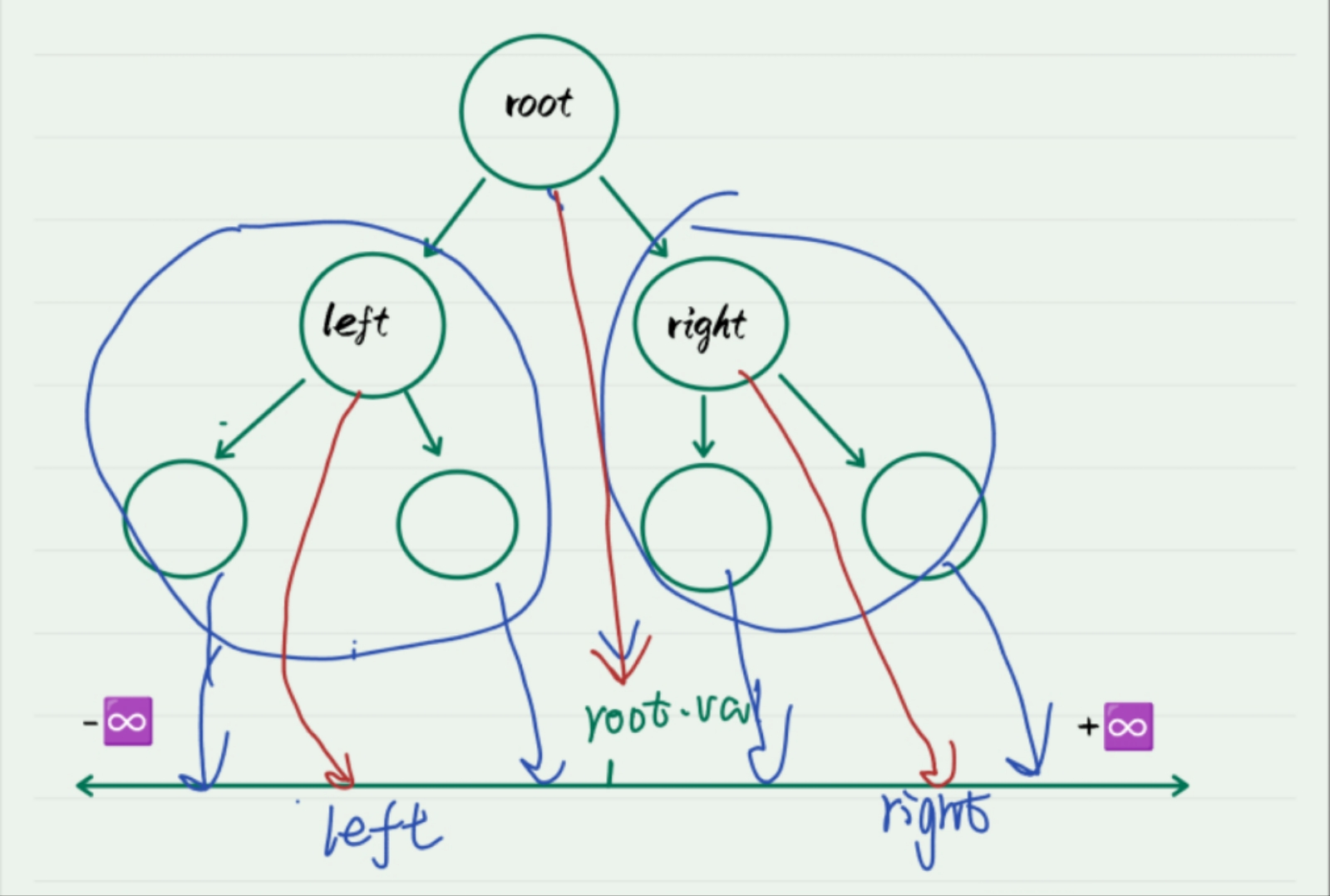
代码

var isValidBST = function(root,left = -Infinity,right = Infinity){
    if(!root){
        return true
    }
    if(left>=root.val||root.val>=right){
        return false
    }
    return isValidBST(root.left,left,root.val)&&isValidBST(root.right,root.val,right)
}