计算机图形学games103——非线性优化

现在做有限元的paper重点就在于优化，例如几万个四面体如何去做实时模拟（手术训练器所需要的）

模型上的创新点已经不太多了，更加重点优化的就剩下了效率问题和准确性的提升

在效率优化方面就有比较重要的非线性优化问题，所谓的非线性优化问题，就是我们如何取得函数的最小值

例如，梯度下降法（机器学习）梯度下降法的思想很简单，就是如何计算点的梯度，梯度代表了该点最快上升的方向，我减去这个方向那就是最快下降的位置，反复多次迭代后，逼近最小值

如下图所示，使用梯度下降有一个问题，如果步长太大，效果会降低，如果太小，会浪费性能，所以如何选择一个良好的step_size是问题的关键之一（果然宇宙的所有问题的难点都包含调参）

有两种方法，精确法和尝试法（步长首先大，而且大的同时能往下走就ok了

如何判断每一步都在下降呢，只有这样我才能保证收敛，条件可以利用是否在同侧判断，也就是通过点乘计算器=其是否大于0就可以判断了

有了每次都下降的步长后，就可以实现下降方法

下降法就包括梯度下降法，牛顿法（hessian矩阵正定），任何利用一个正定矩阵去修改梯度的方法都可认为是下降法，这些下降法是P也就是正定矩阵不一样，不同的方法会有不同的效率

牛顿法的计算时间很长，开销很大，怎么在迭代次数和计算复杂度之间做平衡

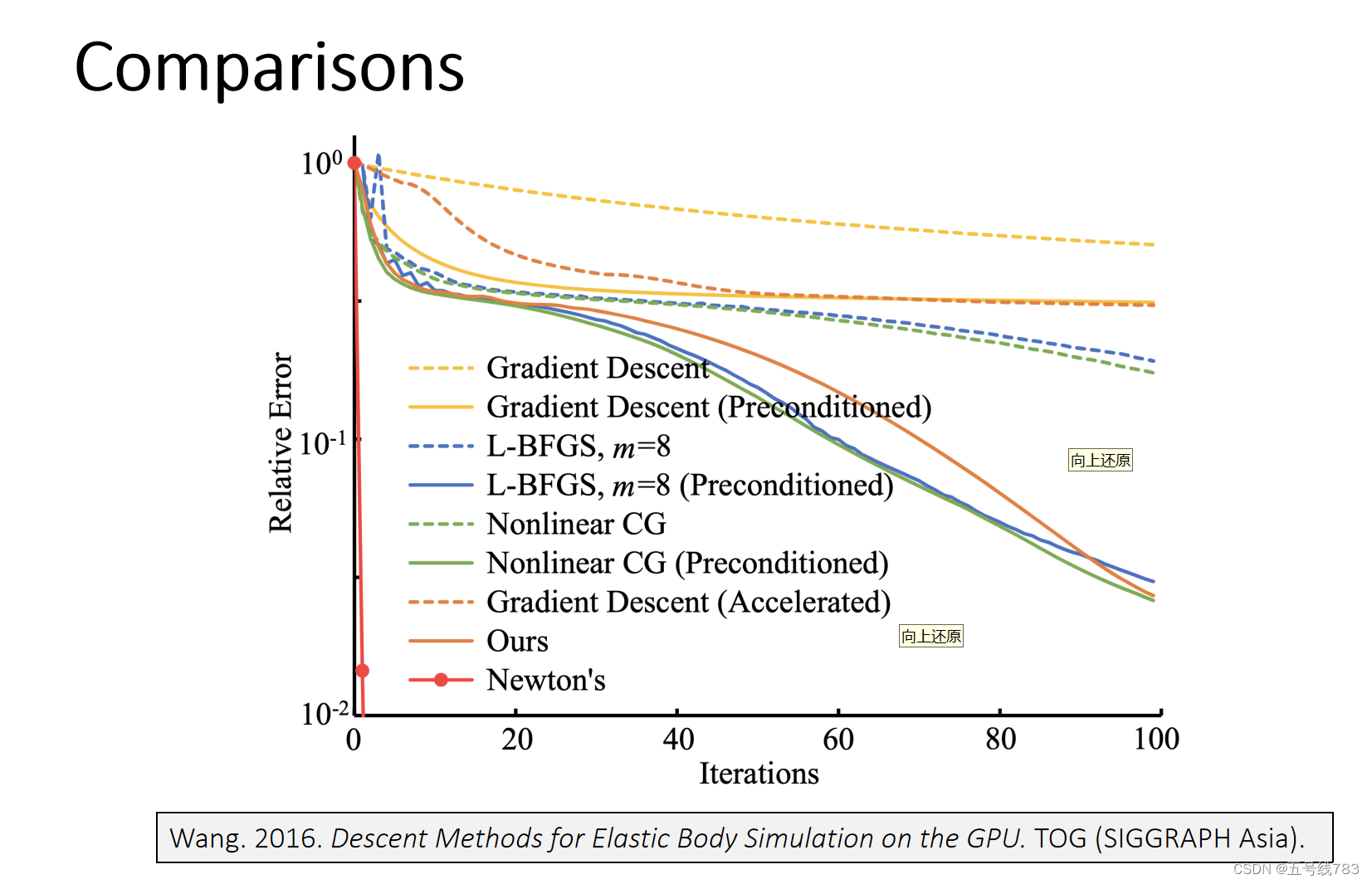
非线性优化的求解方法

1. 梯度下降法：这是最常用的方法之一，通过不断沿梯度方向下降来找到局部最小值。

   优点：简单易实现，适用于大多数问题。

   缺点：可能陷入局部最小值，收敛速度可能较慢。

2. 牛顿法：利用二阶导数信息进行优化，收敛速度快，但计算复杂度高。

   优点：收敛速度快，对局部二次近似良好的问题效果好。

   缺点：需要计算二阶导数，计算量大，不适用于高维问题。

3. 进化算法：如遗传算法和粒子群优化等，模拟自然进化过程进行全局优化。

   优点：不依赖梯度信息，适用于复杂和非连续问题。

   缺点：计算资源需求高，参数设置复杂。

4. 模拟退火：通过模拟物理退火过程，在解空间中进行随机搜索，逐步降温找到最优解。

   优点：具有全局搜索能力，不易陷入局部最优。

   缺点：需要合理设置温度下降策略，计算时间较长。

直观理解

想象你在一片山地上行走，目标是找到山谷的最低点。这片山地有许多山峰和山谷，而你只有当前所在位置的局部地形信息。你可以选择不同的策略，比如：

• 梯度下降法：你每一步都沿着最陡峭的下坡走，这样可以快速下降，但可能会困在局部最低点。
• 牛顿法：你不仅看当前的坡度，还考虑曲率信息，尝试快速找到最低点。
• 进化算法：你和一群人分散在不同的地方，同时寻找最低点，并不断交流信息以改进搜索策略。
• 模拟退火：你一开始大范围搜索，逐渐缩小搜索范围，最后集中精力在潜在的最低点附近仔细寻找。