为什么要做稀疏矩阵,在原生的太极中搭建稀疏矩阵并不是一个简单的事情
太极可以搭建稀疏矩阵,但需要手写使用之前的高级稀疏数据结构SNode-tree
况且写它的计算方法并不是一件简单的事情
如何搭建一个稀疏矩阵,如何使用稀疏矩阵
首先是创建稀疏矩阵,现在的api版本有所改变,和课件不太一样
import taichi as ti
ti.init(arch=ti.cpu)
n = 4
#第一步,建立稀疏矩阵,定义维度,和里面最多接受的triplets数量,这个定义非0现的行号,列号和值
k = ti.linalg.SparseMatrixBuilder(n,n,max_num_triplets=100)
@ti.kernel
def fill(A:ti.types.sparse_matrix_builder()):
for i in range(n):
A[i,i] += 1
#第二步,将builder用数据填充
fill(k)
print(">>>k.print_triplets()")
k.print_triplets()
#第三步,在builder中返回一个稀疏矩阵
A = k.build()
print(">>>A = k.build()")
print(A)现在在api中可以实现加减,矩阵的乘法(与矩阵,与矩阵逐项乘积),A@B是矩阵乘法包括向量,最后还实现了矩阵转置和元素访问
若是正好访问到一个稀疏矩阵的0元素,它会直接返回0而不会真的去访问
稀疏矩阵线性求解器
一个求解器会分为三块来使用,首先是定义求解器,例如实例代码中选择的求解方式是将矩阵分解为一个下三角矩阵和它转置的乘积,第二步就是求解,再到第三步查看求解是否成功
#factorize
solver = ti.linalg.SparseSolver(solver_type="LLT")#定义求解方式,分解矩阵
solver.analyze_pattern(A)#分析给的矩阵进行预分解,不涉及数值
solver.factorize(A)#进行数值分解,将数值存入分解出的矩阵当中
#solve
x = solver.solve(b)#b为待解的向量,可以为一个ti.field,也可以是numpy数组
#check stas 查看求解是否成功
issubclass = solver.info()
print(">>>Solve sparse lineaar sysytems Ax = b with the solution x:")
print(x)
print(">>>Cpmputation was successful?: {issubclass}")简单的例子

复杂一点的例子,关于热传导



那么基于此的稀疏矩阵大致为
 从中心点开始,每一个点会朝着邻居的点施加温度(+1),并在自己的点减去施加温度的4倍,这两者是等价的
从中心点开始,每一个点会朝着邻居的点施加温度(+1),并在自己的点减去施加温度的4倍,这两者是等价的

由于K值的变化,温度扩算会受到影响

我们使用的是显式积分方式来传播温度的
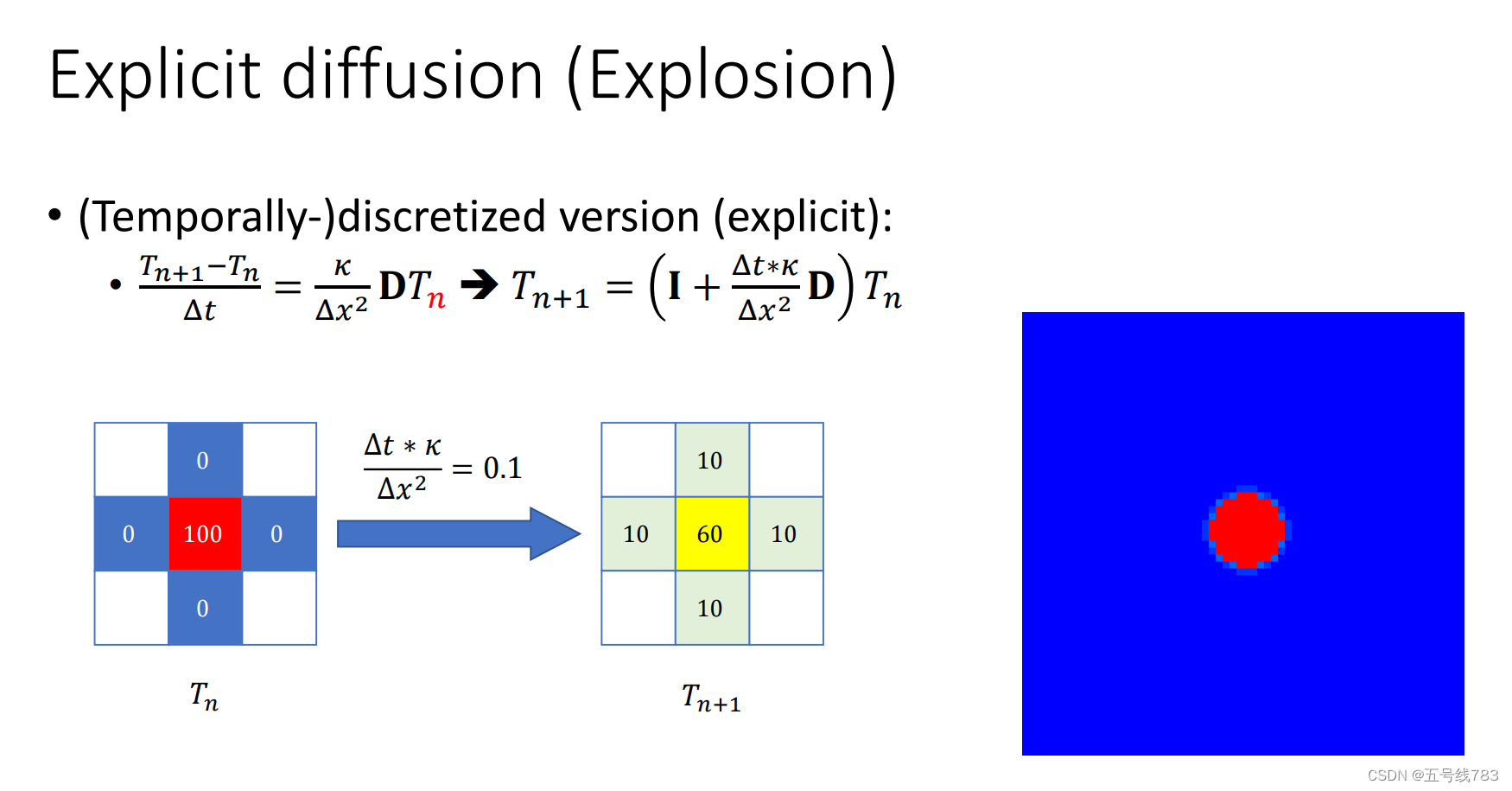
看起来可行,但是如果k过大就会造成问题

所以我们应该用的是下一个时刻的温度进行传导,那么此时我们可以得出的就是一个线性求解的问题

课程中有一些例子,除了热传导外,主要还可以用来作为弹簧质点系统的仿真,稳定流体仿真等
目前只支持cpu的计算,效率也不太高,更多的是用来作为一个验证想法的正确性
如果真的要使用高效率的话需要手写或用一些其他的方法来完成
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








