Pytorch框架与经典卷积神经网络学习Day1|CNN卷积神经网络算法原理

跟学视频

炮哥带你学_Pytorch框架与经典卷积神经网络与实战

1.全连接神经网络的整体结构

有输入层、隐藏层和输出层。

输入的x往往是一个矩阵，如图像、音频等。

2.全连接神经网络的结构单元

a是矩阵。

找出一组最优的w和b。

3.激活函数

3.1为什么激活函数一般选择非线性

使用线性函数，n层神经网络可以转化成一层，只需改变参数。 

使用非线性函数可以体现神经网络的深度。（这是在有限条件下的，如在ResNet中，保证神经网络越深效果不下降且越好。）

3.2经典的激活函数

激活函数没有最优只有最合适。

sigmoid函数

输出层的一个函数

导函数两端导数趋近于0，梯度消失，w和b更新缓慢，难以找到最优的w和b。

值域0~1，适合做分类

Tanh函数 

Tanh函数导数值域比Sigmoid函数导数值域大，所以Tanh函数训练轮次比Sigmoid函数少，可以更快找到最优的w和b。

ReLU函数

分段函数

在后续代码使用较多

ReLU函数导数左端等于0，和前两个函数梯度消失不同，为神经元死亡，w和b不是不是更新比较慢而是不更新了。 

ReLU函数导数左端等于1，更新较快，解决了梯度消失问题。

Leaky ReLU函数

改进ReLU函数

a!=0&&a!=1

4.全连接神经网络前向传播 

向前传播本质就是计算函数结果。

训练、推理、测试、验证都有前向传播的过程。

5.神经网络的损失函数

回归问题：输出值是连续的，如预测明天气温，预测前面的人多高。

若算平均误差，正负值相加会对结果产生影响，如（1+0+（-1））/3=0，所以使用均方误差。

均方参数有1/2是为了求导时更好计算。

利用损失函数的反向传播更新w和b，是我们的损失函数越来越小。

不断进行：前向传播——>计算误差——>反向传播

6.梯度下降法

因为w是矩阵，按照普通求最小值方法可能求不出来，所以采用上图方式。

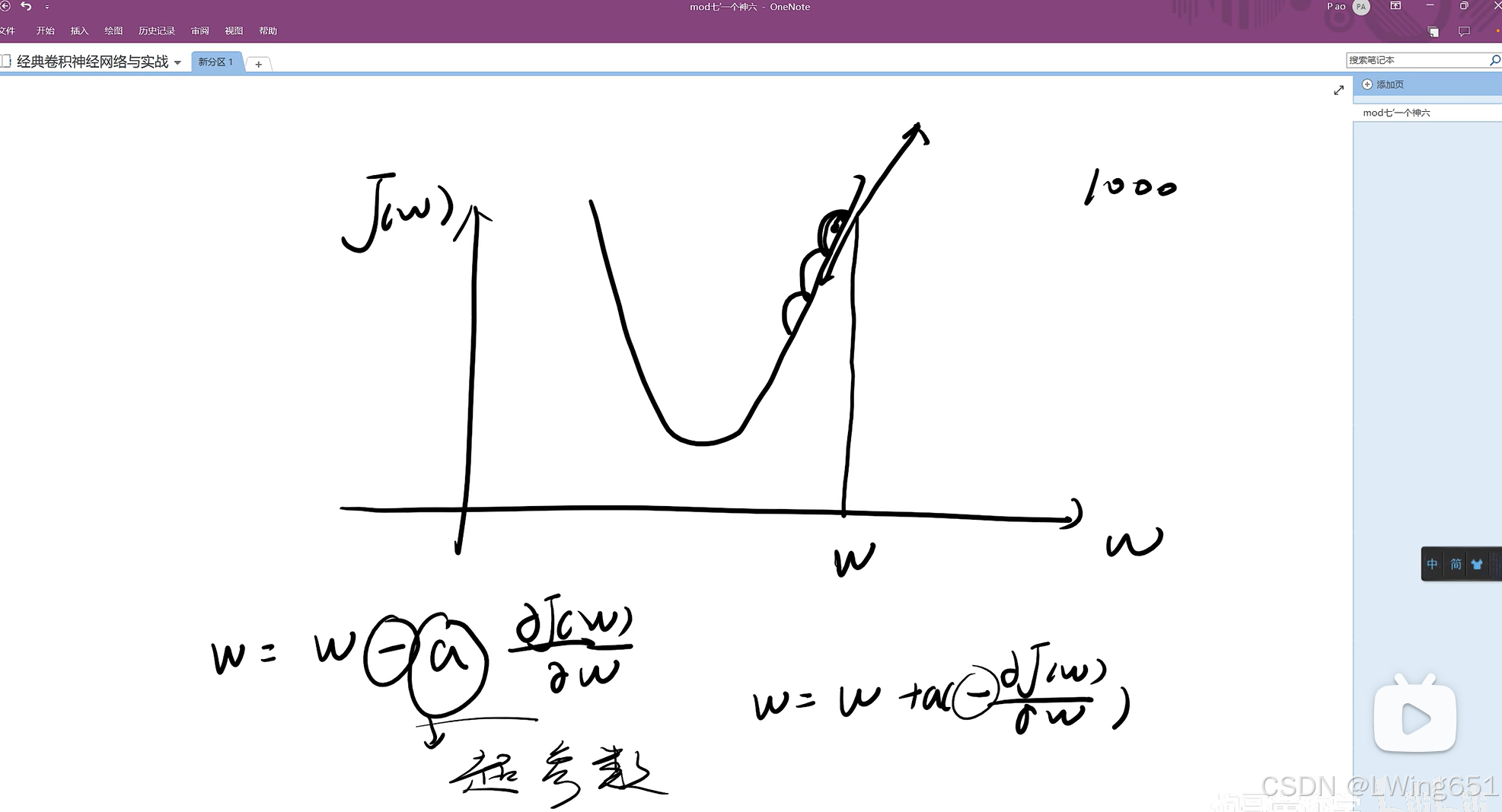
a是超参数（不能过大也不能过小），来设定往下走的距离大不大，即学习率（经验值为0.001~0.05）。

使用同样的方法也可以找到最优的b。

7.反向传播具体计算

一轮后y从1.731变为了1.775，损失变小。

8.整体过程