第一部分:基本含义
Lipschitz 连续性是一种数学概念,用于描述函数的变化率是否受到限制。简单来说,如果一个函数是 Lipschitz 连续的,那么它在定义域内的任何两点之间的输出值的变化不会超过这两个点之间输入值变化的某个固定倍数。这个固定倍数称为 Lipschitz 常数。
第二部分:具体算法
(1)算法
(2)直观理解
-
变化率限制:Lipschitz 连续性意味着函数的变化率不会超过某个上限。换句话说,函数不会在定义域内出现剧烈的波动或突变。
-
几何意义:在几何上,Lipschitz 连续性可以理解为函数图像的斜率不会超过某个固定值。
(3)在机器学习中的应用
在机器学习中,Lipschitz 连续性常用于描述模型的稳定性和泛化能力。例如:
-
模型稳定性:如果一个模型的损失函数是 Lipschitz 连续的,那么在参数空间中的小变化不会导致损失值的剧烈变化,这有助于模型的稳定训练。
-
泛化能力:Lipschitz 连续性与模型的泛化能力有关。平坦的极小值(即损失函数在该区域内的变化较小)通常具有更好的泛化能力,因为它们对参数的小扰动不敏感。
(4)举例
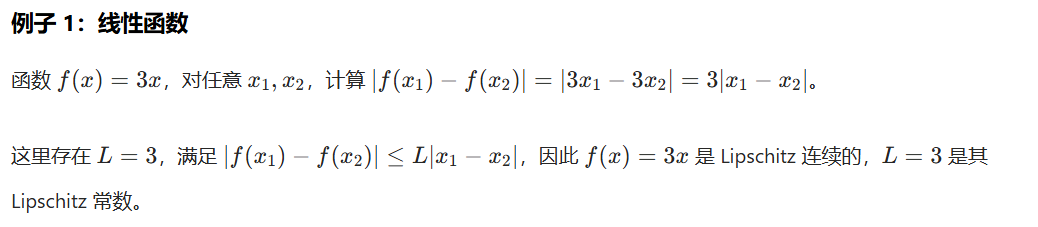



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










