目录
A: 小白鼠
N只小白鼠(1 <= N <= 100),每只鼠头上戴着一顶有颜色的帽子。
现在称出每只白鼠的重量,要求按照白鼠重量从大到小的顺序输出它们头上帽子的颜色。
帽子的颜色用“red”,“blue”等字符串来表示。
不同的小白鼠可以戴相同颜色的帽子。白鼠的重量用整数表示。输入
多案例输入,每个案例的输入第一行为一个整数N,表示小白鼠的数目。
下面有N行,每行是一只白鼠的信息。第一个为不大于100的正整数,表示白鼠的重量;
第二个为字符串,表示白鼠的帽子颜色,字符串长度不超过10个字符。
注意:白鼠的重量各不相同。输出
每个案例按照白鼠的重量从大到小的顺序输出白鼠的帽子颜色。
样例输入 Copy
3 30 red 50 blue 40 green样例输出 Copy
blue green red
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
const int N = 1e3 + 5;
const ll M = 1e9 + 7;
struct stu
{
int b;
char c[15];
}a[105];
bool com(stu a, stu b)
{
return a.b > b.b;
}
void solve(){
int n;
while (~scanf("%d", &n))
{
for (int i = 0; i < n; i++)
scanf("%d %s", &a[i].b, a[i].c);
sort(a, a + n, com);
for (int i = 0; i < n; i++)
printf("%s\n", a[i].c);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
return 0;
}B: 放苹果
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
(用K表示)5,1,1和1,5,1 是同一种分法。输入
每行均包含二个整数M和N,以空格分开。1<=M,N<=10。
输出
对输入的每组数据M和N,用一行输出相应的K。
样例输入 Copy
7 3样例输出 Copy
8
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3 + 5;
int fun(int m,int n){
if(m==0||n==1){
return 1;
}
if(m<n){
return fun(m,m);
}
else{
return fun(m,n-1)+fun(m-n,n);
}
}
void solve(){
int m,n;
while(cin>>m>>n){
cout<<fun(m,n)<<"\n";
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}C: gcd 区间
给定一行 n 个正整数 a[1]..a[n]。
m 次询问,每次询问给定一个区间[L,R],输出 a[L]..a[R]的最大公因数。输入
第一行两个整数 n,m。
第二行 n 个整数表示 a[1]..a[n]。
以下 m 行,每行 2 个整数表示询问区间的左右端点。
保证输入数据合法。
1 <= n <= 1000,1 <= m <= 1,000,000 0 < 数字大小 <= 1,000,000,000输出
共 m 行,每行表示一个询问的答案。
样例输入 Copy
5 3 4 12 3 6 7 1 3 2 3 5 5样例输出 Copy
1 3 7
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
using namespace std;
typedef long long ll;
const int N = 1e3 + 5;
const ll M = 1e9 + 7;
int a[N][N];
int gcd(int a,int b) {
return b>0 ? gcd(b,a%b):a;
}
void solve(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i][i];
}
for(int i=1;i<n;i++){
for(int j=i+1;j<=n;j++){
a[i][j]=gcd(a[i][j-1],a[j][j]);
}
}
while(m--){
int x,y;
cin>>x>>y;
cout<<a[x][y]<<"\n";
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
return 0;
}D: 找宝箱
作为一个强迫症患者,小明在走游戏里的迷宫时一定要把所有的宝箱收集齐才肯罢休。
现在给你一个 N×M 的迷宫,里面有障碍、空地和宝箱,小明在某个起始点,每一步小明可以往上、下、左、右走,当然前提是没有走出迷宫并且走到的点不是障碍。如果小明走到了某个为宝箱的点,那么这个宝箱就被他收集到了,然后此处变为空地。
现在你需要计算小明最少需要走多少步才能收集齐所有的宝箱。输入
输入共有两行。
第一行一个两个正整数 N 和 M,表示迷宫大小。
接下来 N 行,每行 M 个整数,第 i+1 行的第 j 个整数表示迷宫第 i 行第 j 列的情况, 0 表示空地,-1 表示障碍,1 表示宝箱,2 表示小明的起始点。保证 2 只有一个。
1≤N,M≤100,宝箱个数不超过5个。输出
一行一个整数,表示小明最少的步数。如果无法收集齐所有宝箱,输出-1。
样例输入 Copy
3 5 1 -1 1 -1 2 0 -1 0 -1 0 0 0 0 0 0样例输出 Copy
12
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
bool st[105][105][32];
int n,m;
int dx[]={-1,0,1,0};
int dy[]={0,-1,0,1};
struct S{
int x,y;
int st;//状态码
int ss;
};
void solve(){
cin>>n>>m;
vector<vector<int>> a(n,vector<int>(m));
vector<vector<int>> b(n,vector<int>(m,-1));//存宝箱编号
vector<pair<int,int>> c;//收集宝箱坐标,0~size-1
int x=-1,y=-1;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cin>>a[i][j];
if(a[i][j]==2){
x=i;
y=j;
}
else if(a[i][j]==1){
c.push_back({i,j});
b[i][j]=c.size()-1;
}
}
}
int k=c.size();
if(k==0){
cout<<"0\n";
return;
}
queue<S> q;
q.push({x, y,0,0});
st[x][y][0]=true;
int ans=-1;
int s=(1<<k)-1;//全1
while(!q.empty()){
auto t=q.front();
q.pop();
if(t.st==s){
cout<<t.ss<<"\n";
return;
}
for(int i=0;i<4;i++){
int xx=dx[i]+t.x;
int yy=dy[i]+t.y;
if(xx<0||xx>=n||yy<0||yy>=m||a[xx][yy]==-1){
continue;
}
int sst=t.st;
int id=b[xx][yy];
if(id!=-1){
if(!(sst&(1<<id))){
sst|=(1<<id);
}
}
if(!st[xx][yy][sst]){
st[xx][yy][sst]=true;
q.push({xx,yy,sst,t.ss+1});
}
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}E: 游船出租
现有公园游船租赁处请你编写一个租船管理系统。
当游客租船时,管理员输入船号并按下S键,系统开始计时;
当游客还船时,管理员输入船号并按下E键,系统结束计时。
船号为不超过100的正整数。当管理员将0作为船号输入时,
表示一天租船工作结束,系统应输出当天的游客租船次数和平均租船时间。
注意:由于线路偶尔会有故障,可能出现不完整的纪录,即只有租船没有还船,
或者只有还船没有租船的纪录,系统应能自动忽略这种无效纪录。
[注意]:每天的船只互不影响,比如第一天租了船1没有归还,第二天船1应该按照没有借处理。输入
测试输入包含若干测试用例,每个测试用例为一整天的租船纪录,格式为:
船号(1~100) 键值(S或E) 发生时间(小时:分钟)
每一天的记录保证按时间递增的顺序给出。当读到船号为-1时,全部输入结束,相应的结果不要输出。输出
对每个测试用例输出1行,即当天的游客租船次数和平均租船时间(以分钟为单位的精确到个位的整数时间,向上取整)。
样例输入 Copy
1 S 08:10 2 S 08:35 1 E 10:00 2 E 13:16 0 S 17:00 0 S 17:00 3 E 08:10 1 S 08:20 2 S 09:00 1 E 09:20 0 E 17:00 -1样例输出 Copy
2 196 0 0 1 60
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
void solve(){
int n;
unordered_map<int ,string> mp;
vector<int> s;
while(cin>>n&&n!=-1){
string op,t;
cin>>op>>t;
if(n==0){
int k=s.size();
if(k==0){
cout<<"0 0\n";
}
else{
int ss=0;
for(auto i:s){
ss+=i;
}
cout<<k<<" "<<(ss+k-1)/k<<"\n";
}
mp.clear();
s.clear();
}
else{
if(op=="S"){
if(mp[n]==""){
mp[n]=t;
}
}
else{
if(mp[n]!=""){
string a=mp[n];
int t1=((a[0]-'0')*10+a[1]-'0')*60+((a[3]-'0')*10+a[4]-'0');
int t2=((t[0]-'0')*10+t[1]-'0')*60+((t[3]-'0')*10+t[4]-'0');
s.push_back(t2-t1);
mp[n]="";
}
}
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}F: 数字交换
输入一个数n,然后输入n个数值各不相同,调换数组中最大和最小的两个数,然后输出。
输入
测试数据有多组,输入n(1<=n<=20),接着输入n个数。
输出
对于每组输入,输出交换后的结果。
样例输入 Copy
2 1 3样例输出 Copy
3 1
#include<stdio.h>
int main() {
int i, t, max, min, a[25], n;
max = min = 0;
while (scanf("%d", & n) != EOF) {
for (i = 0; i < n; i++) {
scanf("%d", & a[i]);
if (a[i] > a[max])
max = i;
else
if (a[i] < a[min])
min = i;
}
t = a[max];
a[max] = a[min];
a[min] = t;
max = min = 0;
for (i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
}
return 0;
}G: 搬水果
在一个果园里,小明已经将所有的水果打了下来,并按水果的不同种类分成了若干堆,小明决定把所有的水果合成一堆。
每一次合并,小明可以把两堆水果合并到一起,消耗的体力等于两堆水果的重量之和。
当然经过 n‐1 次合并之后,就变成一堆了。小明在合并水果时总共消耗的体力等于每次合并所耗体力之和。
假定每个水果重量都为 1,并且已知水果的种类数和每种水果的数目。
你的任务是设计出合并的次序方案,使小明耗费的体力最少,并输出这个最小的体力耗费值。
例如有 3 种水果,数目依次为 1,2,9。可以先将 1,2 堆合并,新堆数目为3,耗费体力为 3。
然后将新堆与原先的第三堆合并得到新的堆,耗费体力为 12。
所以小明总共耗费体力=3+12=15,可以证明 15 为最小的体力耗费值。输入
每组数据输入包括两行,第一行是一个整数 n(1<=n<=10000),表示水果的种类数。
第二行包含 n 个整数,用空格分隔,第 i 个整数(1<=ai<=1000)是第 i 种水果的数目。输出
对于每组输入,输出一个整数并换行,这个值也就是最小的体力耗费值。
输入数据保证这个值小于 2^31。样例输入 Copy
3 9 1 2 0样例输出 Copy
15
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
void solve(){
int n;
while(cin>>n&&n){
vector<int> a(1001,0);
queue<int> q,qq;
for(int i=1;i<=n;i++){
int x;
cin>>x;
a[x]++;
}
for(int i=1;i<=1000;i++){
while(a[i]>0){
a[i]--;
q.push(i);
}
}
int sum=0;
int x,y;
for(int i=1;i<n;i++){
if((q.front()<qq.front()&&!q.empty())||qq.empty()){
x=q.front();
q.pop();
}
else {
x=qq.front();
qq.pop();
}
if((q.front()<qq.front()&&!q.empty())||qq.empty()) {
y=q.front();
q.pop();
}
else {
y=qq.front();
qq.pop();
}
sum+=x+y;
qq.push(x+y);
}
cout<<sum<<"\n";
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}H: 打牌
牌只有1到9,手里拿着已经排好序的牌a,对方出牌b,用程序判断手中牌是否能够压过对方出牌。
规则:出牌牌型有5种。
[1] 一张 如4 则5...9可压过
[2] 两张 如44 则55,66,77,...,99可压过
[3] 三张 如444 规则如[2]
[4] 四张 如4444 规则如[2]
[5] 五张 牌型只有12345 23456 34567 45678 56789五个,后面的比前面的均大。输入
输入有多组数据。
每组输入两个字符串(字符串大小不超过100)a,b。
a字符串代表手中牌,b字符串代表出的牌。输出
压过输出YES 否则NO。
样例输入 Copy
12233445566677 33样例输出 Copy
YES
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e4 + 5;
int c[15];
void solve(){
string a,b;
while(cin>>a>>b){
if(a.size()<b.size()){
cout<<"NO\n";
}
else{
memset(c,0,sizeof c);
for(int i=0;i<a.size();i++){
c[a[i]-'0']++;
}
if(b.size()==5){
if(b[0]=='5'){
cout<<"NO\n";
}
else{
bool t=false;
for(int i=b[0]-'0'+1;i<6;i++){
if(c[i]&&c[i+1]&&c[i+2]&&c[i+3]&&c[i+4]){
t=true;
cout<<"YES\n";
break;
}
}
if(!t){
cout<<"NO\n";
}
}
}
else{
if(b[0]=='9'){
cout<<"NO\n";
}
else{
bool t=false;
for(int i=b[0]-'0'+1;i<10;i++){
if(c[i]>=b.size()){
t=true;
cout<<"YES\n";
break;
}
}
if(!t){
cout<<"NO\n";
}
}
}
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}I: 狮子座的失眠
狮子座自从上次几乎素数问题没有解决后,开始了失眠之夜,于是他开始了念数字游戏,不过他念的方式很奇妙,他念的是每个数字的拼音,例如:-600 他念的是“fu liu ling ling”。
输入
输入一个整数,保证最多只有4位数,输出每个数字对应的拼音。当整数为负数时,先输出fu字。
输出
在一行中输出这个整数对应的拼音,每个数字的拼音之间用空格分开,行末没有最后的空格。如 yi er san si。
样例输入 Copy
-600样例输出 Copy
fu liu ling ling
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int N = 2e4 + 5;
char c[10][10]={"ling","yi","er","san","si","wu","liu","qi","ba","jiu"};
void solve(){
int n,a[20],i=1;
cin>>n;
if(n<0)
{
cout<<"fu"<<" ";
n=-n;
}
a[0]=n%10;
while(n/10>0)
{
n/=10;
a[i]=n%10;
i++;
}
for(int j=i-1;j>0;j--)
cout<<c[a[j]]<<" ";
cout<<c[a[0]]<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}J: 狮子座的简单统计题
编写程序统计每种不同的个位数字出现的次数。例如:给定 N=100311,则有 2 个 0,3 个 1,和 1 个 3。
输入
每个输入包含 1 个测试用例,即一个不超过 1000 位的正整数 N。
输出
对 N 中每一种不同的个位数字,以 D:M 的格式在一行中输出该位数字 D 及其在 N 中出现的次数 M。要求按 D 的升序输出。
样例输入 Copy
100311样例输出 Copy
0:2 1:3 3:1
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int N = 2e4 + 5;
void solve(){
char n;
int a[10]={0};
while(cin>>n)
a[n-'0']++;
for(int i=0;i<10;i++)
if(a[i]!=0)
cout<<i<<":"<<a[i]<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}K: 狮子座的复杂统计题
狮子座很快就把简单统计题ac了,现在他遇到了一个复杂的统计题。
有一组数据,你需要编程来求出次数出现最多的数字,保证输入是从小到大排序好了的。
如果有两个元素值出现的次数相同,即并列第一,那么只打印比较小的那个值。输入
第一行输入一个整数 N ,N<=20 ,接下来有N个数字,保证从小到大排序,保证都在 int 范围内。
输出
输出只有一行,即出现次数最多的那个元素值。如果次数相同,输出较小的那个值。
样例输入 Copy
5 100 150 150 200 250样例输出 Copy
150
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int N = 2e4 + 5;
void solve(){
int n,a[20],s=1,x,j=0;
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i];
for(int i=1;i<n;i++)
{
if(a[i]==a[i-1])
s++;
else
{
if(s>j)
{
x=a[i-1];
j=s;
}
s=1;
}
}
cout<<x<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}L: 狮子座的水题
狮子座最近在OJ做了一道最小公倍数的题,ac之后特别有成就感,还发现了gcd函数,于是他觉得最小公倍数问题都是水题了。突然,一个叫“欧几里得”的dalao重新排了一道关于最小公倍数的题,题目如下:求出n个数的最小公倍数。 于是,狮子座顿时方了,他只会求两个数的最小公倍数。此时向你求助,请帮助他完成这道题。
输入
输入包含多个测试实例,每个测试实例的开始是一个正整数n,然后是n个正整数。保证都处于int范围内。
输出
为每组测试数据输出它们的最小公倍数,每个测试实例的输出占一行。
样例输入 Copy
2 4 6样例输出 Copy
12
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int N = 2e4 + 5;
int gcd(int a,int b) {
return b>0 ? gcd(b,a%b):a;
}
void solve(){
int n,a,i,x;
while(cin>>n)
{
cin>>a;
i=n-1;
for(int j=0;j<i;j++)
{
cin>>x;
a=a*x/gcd(a,x);
}
cout<<a<<"\n";
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}M: 幸运数
众所周知,不管是人还是熊都需要人品。于是乎,为了给自己找一个幸运数字,Mavis 学习了人类的阿拉伯数字,并不知从哪儿弄来了一串序列和一个 S,Mavis 说:“长度最短且和大于等于 S 的连续子段的长度, 就是俺的幸运数字”!
但是 Mavis 只会喊口号,不会解决问题,所以这个问题就交给你了。输入
输入文件共三行。
第一行输入仅一个正整数 n,意义如题所述。( n ≤ 4000000, ai ≤ 10^9)
第二行输入 n 个正整数 ai,表示序列中的元素。
第三行输入仅一个正整数 S,意义如题所述。
每两个输入的数之间都用一个空格隔开。输出
输出文件仅一行一个整数,表示幸运数。
样例输入 Copy
8 4 12 10 18 17 10 17 17 40样例输出 Copy
3
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <algorithm>
#include <cstring>
#include <queue>
#include <stack>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int N = 4e6 + 5;
ll a[N];
void solve(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
ll s;
cin>>s;
ll i=1,j=1;
ll sum=a[1];
ll ss=1e17;
while(j<=n){
if(sum>=s){
ss=min(ss,j-i+1);
sum-=a[i];
i++;
}
else{
j++;
sum+=a[j];
}
}
if(ss==1e17){
ss=0;
}
cout<<ss<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}N: 跳跃版图
有一个 n×n 的格子,每个格子中有一个非负整数。你的目标是从左上角跳到右下角,每步只能向右或向下跳。格子中的数代表从该格开始跳跃的前进步数,如果某次跳跃会跃出格子 界限则该跳跃是禁止的。注意 0 是一个绝对终点,因为从这里无法再移动。
你的任务是统计有多少种合法路径。上图 1 中共有 3 种路径,分别表示在图 2 中。
输入
第一行,一个整数 n(3 ≤ n ≤ 100)。
接下来 n 行 n 列,表示格子中的数,所有数的范围在[0,9]中,两个数之间用一个空格隔开。输出
第一行,从左上角到右下角的合法路径数目。
样例输入 Copy
4 2 3 3 1 1 2 1 3 1 2 3 1 3 1 1 0样例输出 Copy
3
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
string fun(string a,string b){
string s;
int t=0;
int i=a.size()-1,j=b.size()-1;
while(i>=0||j>=0||t){
int sum=t;
if(i>=0){
sum+=a[i--]-'0';
}
if(j>=0){
sum+=b[j--]-'0';
}
t=sum/10;
s.push_back((sum%10)+'0');
}
reverse(s.begin(), s.end());
return s;
}
void solve(){
int n;
cin>>n;
vector<vector<int>> a(n,vector<int>(n));
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>a[i][j];
}
}
vector<vector<string>> dp(n,vector<string>(n,"0"));
dp[0][0]="1";
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(dp[i][j]=="0"||a[i][j]==0){
continue;
}
int x=j+a[i][j];
if(x<n){
dp[i][x]=fun(dp[i][x],dp[i][j]);
}
int y=i+a[i][j];
if(y<n){
dp[y][j]=fun(dp[y][j],dp[i][j]);
}
}
}
cout<<dp[n-1][n-1]<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}O: 耶路撒冷战役
第二次十字军东征末期,由阿拉伯领袖萨拉丁率领的阿拉伯联军兵临圣城耶路撒冷。在城内驻扎的圣殿骑士团被歼灭之后,阿拉伯大军兵临城下。
来到山岗上,萨拉丁极目远眺,见两小儿辩日, 发现自己的军队排成了一个 NM 大小的方阵。作为一个的军事家,这种阵型是他非常抵触的。于是他打算将他的军队分割成1*1大小的小队。
然而拆分整编的军队是很费时间的一件事,对于行与行之间的每一条横线,列与列之间的每一条竖线,都有一个耗费时间的值(可以相同)。更加麻烦的是,拆分后的军队都是独立的,两个独立的部分不能拼接在一起拆分(比如一个显示器被拆成了两半,想把它拆成四份则需要对于已有的两份分别再拆一次) 。
现在萨拉丁知道每一条横线和每一条竖线耗费时间的值,但是他很忙,所以不能处理出将NM的方阵拆成1*1的小队的总消耗时间的最小值,于是他转向你帮忙。输入
第一行包含两个数N与M,分别表示行和列的数量。
接下来N-1行,表示每一条横线的耗费时间值。
接下来M-1行,表示每一条竖线的耗费时间值。
1 <= N , M <= 2000输出
一个数表示总耗费时间的最小值。
样例输入 Copy
2 2 3 3样例输出 Copy
9
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
void solve(){
int n,m;
cin>>n>>m;
vector<int> a(n-1),b(m-1);
for(int i=0;i<n-1;i++){
cin>>a[i];
}
for(int i=0;i<m-1;i++){
cin>>b[i];
}
sort(a.rbegin(),a.rend());
sort(b.rbegin(),b.rend());
ll s=0;
int i=0,j=0;
int x=0,y=0;
while(i<a.size()||j<b.size()){
if(i<a.size()&&(j>=b.size()||a[i]>=b[j])){
s+=(ll)a[i]*(y+1);
x++;
i++;
}
else{
s+=(ll)b[j]*(x+1);
y++;
j++;
}
}
cout<<s<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}P: Fy's dota2
Fy 觉得自己玩 cf,lol这种高端游戏已经够厉害了,于是他决定去玩dota2。结果 fy 的鼠标右键坏了,所以他就等到 2500 买了把闪烁匕首,用跳刀前进,准备去送泉水。但是 fy 一次最多前进 k 的距离,泉水离 fy 现在的距离是 n。
Fy 想知道他到泉水的方案数。输入
第一行 2 个整数:k,n
1<=n<=2^31-1,1<=k<=10输出
一行 1 个整数:代表答案对 7777777 取膜的结果
样例输入 Copy
2 4样例输出 Copy
5
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int inf = 0x3fffffff;
const int P = 13331;
const int MOD = 7777777;
vector<vector<ll>> mul(vector<vector<ll>> a,vector<vector<ll>> b){
int k=a.size();
vector<vector<ll>> s(k,vector<ll>(k,0));
for(int i=0;i<k;i++){
for(int j=0;j<k;j++){
for(int z=0;z<k;z++){
s[i][j]=(s[i][j]+a[i][z]*b[z][j])%MOD;
}
}
}
return s;
}
vector<vector<ll>> m_qpow(vector<vector<ll>> a,int t){
int k=a.size();
vector<vector<ll>> s(k,vector<ll>(k,0));
for(int i=0;i<k;i++){
s[i][i]=1;
}
while(t){
if(t&1){
s=mul(s,a);
}
a=mul(a,a);
t/=2;
}
return s;
}
vector<ll> fun(vector<vector<ll>> a,vector<ll> ss){
int k=a.size();
vector<ll> s(k,0);
for(int i=0;i<k;i++){
for(int j=0;j<k;j++){
s[i]=(s[i]+a[i][j]*ss[j])%MOD;
}
}
return s;
}
void solve(){
int k,n;
cin>>k>>n;
vector<ll> dp(k);
dp[0]=1;
for(int i=1;i<k;i++){
dp[i]=0;
for(int j=0;j<i;j++){
dp[i]=(dp[i]+dp[j])%MOD;
}
}
if(n<k){
cout<<dp[n]%MOD<<"\n";
return;
}
vector<vector<ll>> m(k,vector<ll>(k,0));
for(int i=0;i<k;i++){
m[0][i]=1;
}
for(int i=1;i<k;i++){
m[i][i-1]=1;
}
int t=n-k+1;
vector<vector<ll>> s=m_qpow(m,t);
vector<ll> ss(k);
for(int i=0;i<k;i++){
ss[i]=dp[k-1-i];
}
vector<ll> ans=fun(s,ss);
cout<<ans[0]%MOD<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}Q: 河畔军训
河畔镇是一个景色秀丽,气候宜人的度假胜地,每天都会有很多的游客来这里游玩。但奇怪的是这里总会出现一些潜伏者。果不其然,通过保卫者的跟踪,发现在河畔镇的地下隐藏着Blitz的秘密武器实验室。最危险的地方也是最安全的地方,这里人多,所以只能采用狙击作战,一场“无声无息“的战斗即刻打响。
每到周末小z,小y便开始在河畔军训小h(当然有时也会被反军训)。
不过他们军训采用刀战(即相遇时才可军训)
每当小z,小y,小h三人在河畔整相遇时,小z和小y便可军训小h
由于小h有兔耳朵buff加成,小h每秒最多可以移动3步,且可以选择上/下/左/右/左上/左下/右上/右下8个方向移动
小z,小y每秒均只能移动1步,只能上/下/左/右4个方向移动。
当然,三人均可选择保持原地不动。
三人移动始终在地图范围内。
下面,给你河畔的地图以及小z,小y,小h的初始坐标。
请你求出最快军训小h的时间(即3人相遇的最短时间),如果无法军训小h则输出“lack of junxun”输入
多组数据
每组数据第一行两个整数N,M(1<=N,M<=1000)代表河畔地图的行和列
接下来是N*M大小的地图
其中“z”,“y”,“h”分别代表小z,小y,小h的初始坐标
“#”代表障碍物,“.”表示可以正常通过的位置输出
对于每组数据
如果能军训小h,则输出最快军训小h所需的时间
否则,输出“lack of junxun”样例输入 Copy
2 4 z..h #y#. 2 3 z#y #h.样例输出 Copy
1 lack of junxun
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int inf = 0x3fffffff;
const int P = 13331;
const int MOD = 7777777;
int d4[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
int d8[8][2]={{-1,0},{1,0},{0,-1},{0,1},{-1,-1},{-1,1},{1,-1},{1,1}};
int n,m;
struct S{
int x,y;
};
vector<vector<int>> bfs1(vector<string> a,int x,int y){
vector<vector<int>> dis(n,vector<int>(m,inf));
queue<S> q;
dis[x][y]=0;
q.push({x,y});
while(!q.empty()){
auto t=q.front();
q.pop();
for(int i=0;i<4;i++){
int nx=t.x+d4[i][0];
int ny=t.y+d4[i][1];
if(nx>=0&&nx<n&&ny>=0&&ny<m&&a[nx][ny]!='#'&&dis[nx][ny]==inf){
dis[nx][ny]=dis[t.x][t.y]+1;
q.push({nx,ny});
}
}
}
return dis;
}
vector<vector<int>> bfs2(vector<string> a,int x,int y){
vector<vector<int>> dis(n,vector<int>(m,inf));
queue<S> q;
dis[x][y]=0;
q.push({x,y});
while(!q.empty()){
auto t=q.front();
q.pop();
int xx=t.x,yy=t.y;
int s=dis[xx][yy];
for(int i=0;i<8;i++){
int nx=xx+d8[i][0];
int ny=yy+d8[i][1];
if(nx>=0&&nx<n&&ny>=0&&ny<m&&a[nx][ny]!='#'){
if(dis[nx][ny]>s+1) {
dis[nx][ny]=s+1;
q.push({nx,ny});
}
}
}
for(int i1=0;i1<8;i1++){
int nx1=xx+d8[i1][0];
int ny1=yy+d8[i1][1];
if(nx1<0||nx1>=n||ny1<0||ny1>=m||a[nx1][ny1]=='#'){
continue;
}
for(int i2=0;i2<8;i2++){
int nx2=nx1+d8[i2][0];
int ny2=ny1+d8[i2][1];
if(nx2<0||nx2>=n||ny2<0||ny2>=m||a[nx2][ny2]=='#'){
continue;
}
if(dis[nx2][ny2]>s+1) {
dis[nx2][ny2]=s+1;
q.push({nx2,ny2});
}
}
}
for(int i1=0;i1<8;i1++){
int nx1=xx+d8[i1][0];
int ny1=yy+d8[i1][1];
if(nx1<0||nx1>=n||ny1<0||ny1>=m||a[nx1][ny1]=='#'){
continue;
}
for(int i2=0;i2<8;i2++){
int nx2=nx1+d8[i2][0];
int ny2=ny1+d8[i2][1];
if(nx2<0||nx2>=n||ny2<0||ny2>=m||a[nx2][ny2]=='#'){
continue;
}
for(int i3=0;i3<8;i3++){
int nx3=nx2+d8[i3][0];
int ny3=ny2+d8[i3][1];
if(nx3>=0&&nx3<n&&ny3>=0&&ny3<m&&a[nx3][ny3]!='#'){
if(dis[nx3][ny3]>s+1) {
dis[nx3][ny3]=s+1;
q.push({nx3,ny3});
}
}
}
}
}
}
return dis;
}
void solve(){
while(cin>>n>>m){
vector<string> a(n);
int zx,zy;
int yx,yy;
int hx,hy;
for(int i=0;i<n;i++){
cin>>a[i];
for(int j=0;j<m;j++){
if(a[i][j]=='z'){
zx=i;
zy=j;
a[i][j]='.';
}
else if(a[i][j]=='y'){
yx=i;
yy=j;
a[i][j]='.';
}
else if(a[i][j]=='h'){
hx=i;
hy=j;
a[i][j]='.';
}
}
}
vector<vector<int>> disz=bfs1(a,zx,zy);
vector<vector<int>> disy=bfs1(a,yx,yy);
vector<vector<int>> dish=bfs2(a,hx,hy);
int mi=inf;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(disz[i][j]==inf||disy[i][j]==inf||dish[i][j]==inf){
continue;
}
int mm=max(disz[i][j],max(disy[i][j], dish[i][j]));
mi=min(mi,mm);
}
}
if(mi!=inf){
cout<<mi<<"\n";
}
else{
cout<<"lack of junxun\n";
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}R: 小B旅游
小B在一个有N个城市M条道路的国家,每条道路连接的城市可以互相到达且每条道路小B都要花1步去走过它。现在他在1号城市,问他走P步最多能走多少个不同的城市?输入
输入格式:第1行,三个正整数N、M、P,意义如题:接下来M行,每行两个整数U、V,表示存在一条连接U、V的无向边。输出
输出格式:1行,一个整数,表示从1号城市出发走P步的所有情况,共能经过多少个不同的城市。样例输入 Copy
4 4 2 1 2 1 3 2 3 3 4样例输出 Copy
4
提示
数据规模:
1<=N<=100000,1<=M<=5000000,1<=P<=10000
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 1e3+5;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
int n,m,p;
struct S{
int x,y;
};
void solve(){
cin>>n>>m>>p;
vector<vector<int>> a(n+1);
while(m--){
int u,v;
cin>>u>>v;
a[u].push_back(v);
a[v].push_back(u);
}
vector<bool> b(n+1,false);
set<int> st;
queue<S> q;
q.push({1,0});
b[1]=true;
st.insert(1);
while(!q.empty()){
auto t=q.front();
q.pop();
if(t.y>p){
continue;
}
st.insert(t.x);
for(auto xx:a[t.x]){
if(!b[xx]){
b[xx]=true;
q.push({xx,t.y+1});
}
}
}
cout<<st.size()<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}S: 括号匹配
括号主要有:大括号“{ }”、中括号“[ ]”、小括号“( )”。给定一个只包含左右括号的合法括号序列(序列长度2<=n<=10000),按右括号从左到右的顺序输出每一对配对的括号出现的位置(括号序列以0开始编号)
输入
输入格式:仅1行,表一个合法的括号序列
输出
输出格式:设括号序列有n个右括号,每行两个整数l、r,表示配对的括号左括号出现在第l位,右括号出现在第r位。
样例输入 Copy
{()[()()]}()样例输出 Copy
1 2 4 5 6 7 3 8 0 9 10 11
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e4 + 5;
void solve(){
string s;
cin>>s;
stack<int> st;
for(int i=0;i<s.size();i++){
if(s[i]=='{'||s[i]=='['||s[i]=='('){
st.push(i);
}
else if(s[i]=='}'){
int l=st.top();
st.pop();
cout<<l<<" "<<i<<"\n";
}
else if(s[i]==']'){
int l=st.top();
st.pop();
cout<<l<<" "<<i<<"\n";
}
else if(s[i]==')'){
int l=st.top();
st.pop();
cout<<l<<" "<<i<<"\n";
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}T: 正常血压
监护室每小时测量一次病人的血压,若收缩压在90-140之间并且舒张压在60-90之间(包含端点值)则称之为正常。
现给出某病人若干次测量的血压值,计算病人保持连续正常血压的最长小时数。输入
单组输入,每组n+1行。
第一行为一个正整数n(n<100),其后有n行,每行2个正整数,分别为一次测量的收缩压和舒张压。输出
输出仅一行,表示血压连续正常的最长小时数。
样例输入 Copy
4 100 80 90 50 120 60 140 90样例输出 Copy
2
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3 + 5;
void solve(){
int n;
cin>>n;
vector<pair<int,int>> p(n);
for(int i=0;i<n;i++){
cin>>p[i].first>>p[i].second;
}
int s=0;
int m=0;
for(int i=0;i<n;i++){
if(p[i].first>=90&&p[i].first<=140&&p[i].second>=60&&p[i].second<=90){
m++;
s=max(s,m);
}
else{
m=0;
}
}
cout<<s<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}U: 三进制回文数
三进制回文数是指一个三进制数同时又是一个回文数,例如121、102201。
现在输入两个十进制正整数m和n,m<n,请编写一个程序统计在m和n之间(包括m和n)有多少个十进制正整数转换成三进制数之后可以得到三进制回文数。输入
单组输入。
输入两个不超过1000的正整数m和n,m<n,二者之间用英文的空格隔开。输出
输出在m和n之间(包括m和n)的十进制正整数转换成三进制数之后可以得到三进制回文数的个数。
样例输入 Copy
1 10样例输出 Copy
5
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3 + 5;
string fun(int n){
string s="";
while(n){
char t=(n%3+'0');
s+=t;
n/=3;
}
reverse(s.begin(),s.end());
return s;
}
bool fun1(string a){
string b=a;
reverse(a.begin(),a.end());
if(a==b){
return true;
}
return false;
}
void solve(){
int m,n;
cin>>m>>n;
int s=0;
for(int i=m;i<=n;i++){
if(fun1(fun(i))){
s++;
}
}
cout<<s<<"\n";
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}V: hy的战犯评级(Easy)
本题与战犯评级(Hard) 的唯一区别是n的范围。
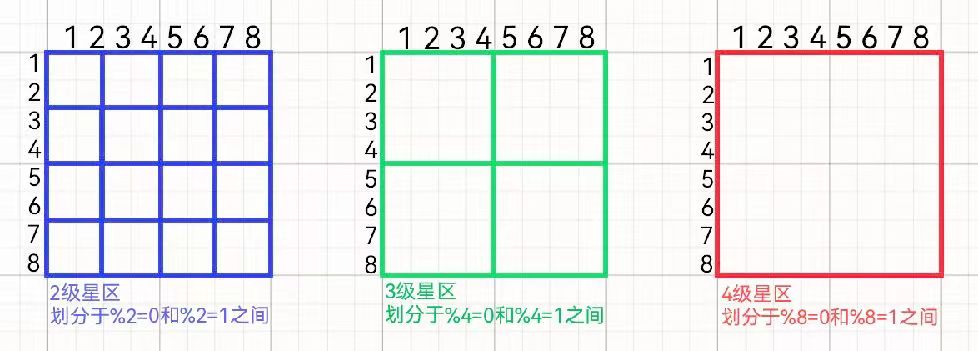
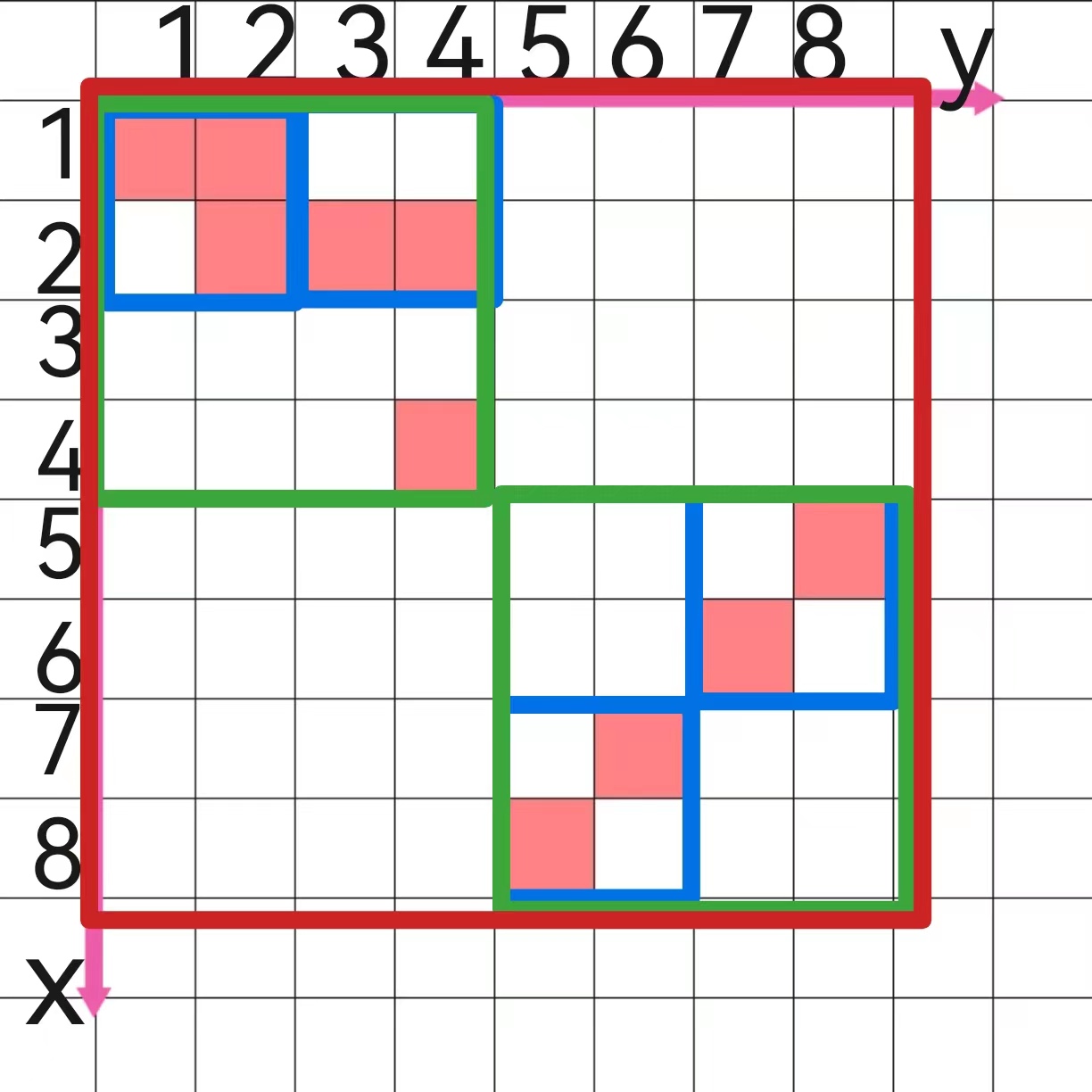
hy最近迷上了科幻小说《银河帝国》,想在银河系大显身手的他启动了《Stellaris》。 在遭到游戏中其他国家的无情羞辱后,开战!开战!一名p社战犯就这么诞生了... hy占领了m个星系,他想知道自己的势力如何,于是发明了战犯评级算法: 银河系是一个2n x 2n大小的矩阵,每个位置有一个星系。定义i级星区为左上角点横纵坐标均mod 2(i-1) = 1,大小 2i-1× 2i-1 的矩阵(如下图);特殊地,1级星区是一个星系。当一个i级星区内至少2个i-1级星区已 占领时,则认为该i级星区已占领 定义战犯等级为占领最大星区的等级,你能求出这个数值,以便在军事法庭上痛斥hy的战争罪 行吗?
输入
每个测试文件仅有一组测试数据。
第一行输入两个整数n,m(0<=n<=10,0<=m<=105)表示银河系是2n × 2n大小的矩阵,已占领m个星 系。
对于接下来m行,第i行输入两个整数xi和yi(1<=xi,yi<=2n),表示占领的第i个星系在银河系中的位 置。输入保证所有位置两两不同。
输出
输出一行一个整数表示hy是几级战犯。
样例输入 Copy
2 6 1 1 1 2 2 2 2 3 2 4 4 4样例输出 Copy
3提示
由于占领了(1,1),(1,2),(2,2)三个星系,因此占领了以(1,1)为左上角的2级星区
由于占领了(2,3),(2,4)两个星系,因此占领了以(1,3)为左上角的2级星区
由于占领了以(1,1)和(1,3)为左上角的二级星区,因此占领了以(1,1)为左上角的3级星
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
void solve(){
int n,m;
cin>>n>>m;
vector<unordered_set<ll>> st(n+2);
for(int i=0;i<m;i++){
int x,y;
cin>>x>>y;
ll k=((ll)x<<16)|y;
st[1].insert(k);
}
if(n==0){
if(m){
cout<<"1\n";
}
else{
cout<<"0\n";
}
return;
}
for(int i=2;i<=n+1;i++){
int k=1<<(i-1);//2的i-1次方
int s=k>>1;
int max=(1<<n)-k+1;//最大有效值
if(max<1){
continue;
}
unordered_set<ll> sst;
for(int j=1;j<=max;j+=k){
for(int z=1;z<=max;z+=k){
int x1=j,y1=z;
int x2=j,y2=z+s;
int x3=j+s,y3=z;
int x4=j+s,y4=z+s;
int cnt=0;
ll k1=((ll)x1<<16)|y1;
if(st[i-1].count(k1)){
cnt++;
}
ll k2=((ll)x2<<16)|y2;
if(st[i-1].count(k2)){
cnt++;
}
ll k3=((ll)x3<<16)|y3;
if(st[i-1].count(k3)){
cnt++;
}
ll k4=((ll)x4<<16)|y4;
if(st[i-1].count(k4)){
cnt++;
}
if(cnt>=2){
ll kk=((ll)j<<16)|z;
sst.insert(kk);
}
}
}
st[i]=sst;
}
for(int i=n+1;i>=1;i--){
if(!st[i].empty()){
cout<<i<<"\n";
return;
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}W: hy的战犯评级(Hard)
本题与战犯评级(Easy) 的唯一区别是n的范围:在Easy版中,n=10。
hy最近迷上了科幻小说《银河帝国》,想在银河系大显身手的他启动了《Stellaris》。 在遭到游戏中其他国家的无情羞辱后,开战!开战!一名p社战犯就这么诞生了... hy占领了m个星系,他想知道自己的势力如何,于是发明了战犯评级算法: 银河系是一个2n x 2n大小的矩阵,每个位置有一个星系。定义i级星区为左上角点横纵坐标均mod 2(i-1) = 1,大小 2i-1× 2i-1 的矩阵(如下图);特殊地,1级星区是一个星系。当一个i级星区内至少2个i-1级星区已 占领时,则认为该i级星区已占领 定义战犯等级为占领最大星区的等级,你能求出这个数值,以便在军事法庭上痛斥hy的战争罪 行吗?
输入
每个测试文件仅有一组测试数据。
第一行输入两个整数n,m(0<=n<=60,0<=m<=105)表示银河系是2n × 2n大小的矩阵,已占领m个星 系。
对于接下来m行,第i行输入两个整数xi和yi(1<=xi,yi<=2n),表示占领的第i个星系在银河系中的位 置。输入保证所有位置两两不同。
输出
输出一行一个整数表示hy是几级战犯。
样例输入 Copy
2 6 1 1 1 2 2 2 2 3 2 4 4 4样例输出 Copy
3提示
由于占领了(1,1),(1,2),(2,2)三个星系,因此占领了以(1,1)为左上角的2级星区
由于占领了(2,3),(2,4)两个星系,因此占领了以(1,3)为左上角的2级星区
由于占领了以(1,1)和(1,3)为左上角的二级星区,因此占领了以(1,1)为左上角的3级星
#include <iostream>
#include <string>
#include <cmath>
#include <set>
#include <map>
#include <algorithm>
#include <cstring>
#include <vector>
#include <stack>
#include <queue>
#include <list>
#include <deque>
#include <bitset>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int uint;
const int N = 3e3+10;
const int M = 1e9+7;
const int inf = 0x3fffffff;
const int P = 13331;
//pair<T1, T2> 类型的哈希值
struct pair_hash {
template<class T1, class T2>
size_t operator() (const pair<T1, T2>& p) const {
auto h1 = hash<T1>{}(p.first);
auto h2 = hash<T2>{}(p.second);
return h1 ^ (h2 << 1);
}
};
void solve(){
int n,m;
cin>>n>>m;
if(n==0){
if(m){
cout<<"1\n";
}
else{
cout<<"0\n";
}
return;
}
unordered_set<pair<ull,ull>,pair_hash> st[62];
for(int i=0;i<m;i++){
ull x,y;
cin>>x>>y;
st[1].insert({x,y});
}
ull t=1LL<<n;
for(int i=2;i<=n+1;i++){
ull k=1LL<<(i-1);
unordered_map<pair<ull,ull>,ull,pair_hash> mp;
for(auto it:st[i-1]){
ull x=it.first;
ull y=it.second;
ull xx=((x-1)/k)*k+1;
ull yy=((y-1)/k)*k+1;
if(++mp[{xx,yy}]==2){
st[i].insert({xx, yy});
}
}
}
for(int i=n+1;i>=1;i--){
if(!st[i].empty()){
cout<<i<<"\n";
return;
}
}
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);
//int T;cin>>T;for(int i=1;i<=T;i++)
solve();
return 0;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








