【c++笔试强训】（第十五篇）

目录

买卖股票的最好时机(⼀)（贪⼼）

题目解析

讲解算法原理

编写代码

过河卒（动态规划-路径问题）

题目解析

讲解算法原理

编写代码

---

买卖股票的最好时机(⼀)（贪⼼）

题目解析

1.题目链接：买卖股票的最好时机(一)_牛客题霸_牛客网

2.题目描述

描述

假设你有一个数组prices，长度为n，其中prices[i]是股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

1.你可以买入一次股票和卖出一次股票，并非每天都可以买入或卖出一次，总共只能买入和卖出一次，且买入必须在卖出的前面的某一天

2.如果不能获取到任何利润，请返回0

3.假设买入卖出均无手续费

数据范围： 0 \le n \le 10^5 , 0 \le val \le 10^40≤n≤105,0≤val≤104

输入描述：

第一行输入一个正整数 n 表示数组的长度

第二行输入 n 个正整数，表示股票在第 i 天的价格

输出描述：

输出只买卖一次的最高收益

示例1

输入：

7
8 9 2 5 4 7 1

输出：

5

说明：在第3天(股票价格 = 2)的时候买入，在第6天(股票价格 = 7)的时候卖出，最大利润 = 7-2 = 5 ，不能选择在第2天买入，第3天卖出，这样就亏损7了；同时，你也不能在买入前卖出股票。            

示例2

输入：

3
2 4 1

输出：

2

示例3

输入：

3
3 2 1

输出：

0

讲解算法原理

解法：
算法思路：
⼩贪⼼：
因为只能买卖⼀次，因此，对于第i天来说，如果在这天选择卖出股票，应该在 [0, i] 天之内，股票最低点买⼊股票，此时就可以获得最⼤利润。
那么，我们仅需维护⼀个前驱最⼩值的变量，并且不断更新结果即可。

编写代码

c++算法代码：

#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int arr[N];
int main()
{
 cin >> n;
 for(int i = 0; i < n; i++) cin >> arr[i];
 int ret = 0, prevMin = arr[0];
 for(int i = 1; i < n; i++)
 {
 prevMin = min(arr[i], prevMin);
 ret = max(ret, arr[i] - prevMin);
 }
 cout << ret << endl;
 return 0;
}

java 算法代码：

import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main
{
 public static void main(String[] args) 
 {
 Scanner in = new Scanner(System.in);
 int n = in.nextInt();
 int ret = 0, prevMin = in.nextInt();
 int x = 0;
 for(int i = 1; i < n; i++)
 {
 x = in.nextInt();
 ret = Math.max(ret, x - prevMin);
 prevMin = Math.min(prevMin, x);
 }
 System.out.println(ret < 0 ? 0 : ret);
 }
}

 

过河卒（动态规划-路径问题）

题目解析

1.题目链接：[NOIP2002 普及组] 过河卒_牛客题霸_牛客网

2.题目描述

描述

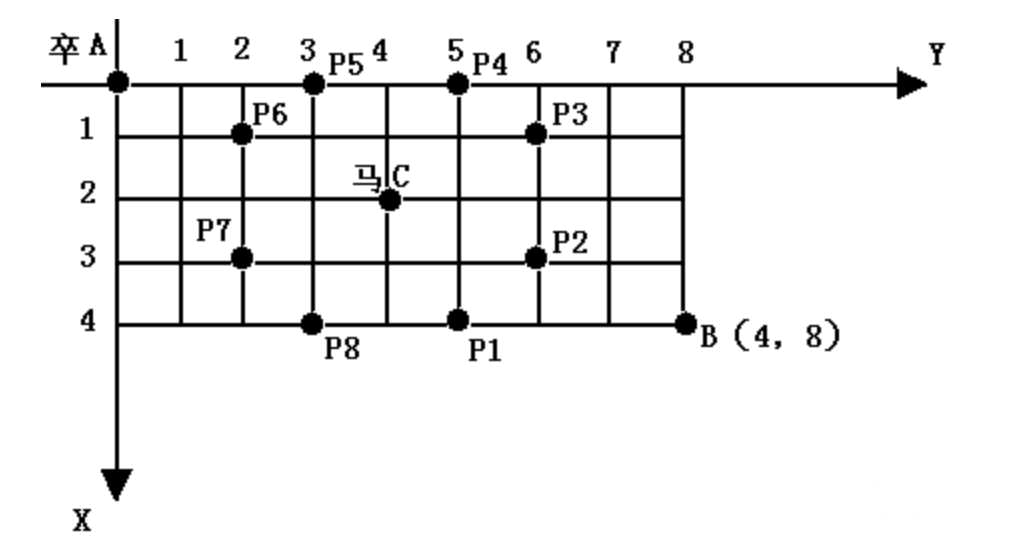
棋盘上 A点有一个过河卒，需要走到目标 B点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0, 0)、B点(n,m)，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 A点能够到达 B点的路径的条数，假设马的位置(x,y)是固定不动的，并不是卒走一步马走一步。

注：马一次跳跃到达的点(x1,y1)和马原坐标(x,y)的关系是 |x1-x|+|y1-y|=3 ，且x1 \neq x ,y1\neq y \∣x1−x∣+∣y1−y∣=3，且x1​=x,y1​=y 

数据范围： 1 \le n,m \le 20\1≤n,m≤20 ，马的坐标 0 \le x,y \le 20 \0≤x,y≤20 

1 \le a,b,c,d \le 1000 \1≤a,b,c,d≤1000 

输入描述：

仅一行，输入 n,m,x,y 四个正整数。分别表示B点坐标和马的坐标

输出描述：

输出路径总数

示例1

输入：

6 6 3 3

输出：

6

示例2

输入：

5 4 2 3

输出：

3

示例3

输入：

2 5 3 5

输出：

1

讲解算法原理

解法：算法思路：
简单路径dp问题：相当于是有障碍物的路径类问题，标记⾛到障碍物上的⽅法数为0即可。

编写代码

c++算法代码：

#include <iostream>
using namespace std;
int n, m, x, y;
long long dp[25][25];
int main()
{
 cin >> n >> m >> x >> y;
 
 x += 1; y += 1;
 dp[0][1] = 1;
 for(int i = 1; i <= n + 1; i++)
 {
 for(int j = 1; j <= m + 1; j++)
 {
 if(i != x && j != y && abs(i - x) + abs(j - y) == 3 || (i == x && 
j == y))
 {
 dp[i][j] = 0;
 }
 else
 {
 dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
 }
 }
 }
 cout << dp[n + 1][m + 1] << endl;
 return 0;
}

java算法代码：

import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main
{
 public static void main(String[] args) 
 {
 Scanner in = new Scanner(System.in);
 int n = in.nextInt(), m = in.nextInt(), x = in.nextInt(), y = 
in.nextInt();
 long[][] dp = new long[n + 2][m + 2];
 dp[0][1] = 1;
 x += 1; y += 1;
 for(int i = 1; i <= n + 1; i++)
 {
 for(int j = 1; j <= m + 1; j++)
 {
 if(i != x && j != y && Math.abs(i - x) + Math.abs(j - y) == 3
|| (i == x && j == y))
 {
 dp[i][j] = 0;
 }
 else
 {
 dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
 }
 }
 }
 System.out.println(dp[n + 1][m + 1]);
 }
}