简化神经元模型2 -- QIF Model_qif模型 brian2实现-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_73557167/article/details/146077495

二次整合发放（QIF）模型

0. 写在前面

前面介绍了Hodgkin-Huxley Model和简化神经元模型1 – LIF Model
下面继续介绍简化神经元模型，本篇博客主要是介绍二次整合发放（Quadratic Integrate-and-Fire, QIF）模型，并用BrainPy实现模型的定义、模拟和分析。

前面介绍的LIF Model在动作点位表征上有一定的缺陷，为了弥补这一缺陷，Latham 等人于 2000 年提出了二次整合发放模型（Quadratic Integrate-and-Fire model，QIF model）。

1. QIF 模型的定义

在 QIF 模型中，微分方程右侧的二阶项使得神经元能产生和真实神经元更“像”的动作电位，
具体动力学方程如下：
$\tau \frac{dV}{dt} = a_0 (V - V_{\text{rest}}) (V - V_c) + RI(t) \tag{1}$ $\text{if } V > \theta, \quad V \leftarrow V_{\text{reset}} \text{ last } t_{\text{ref}} \tag{2}$
方程 (1)中要求 $a_0 > 0$ ， $V_c > V_{\text{rest}}$ 。与LIF模型的动力学方程相比，方程 (1) 右侧是一个关于 $V$ 的二次方程，这使得膜电位的上升有一个从慢到快的过程，与真实的膜电位变化更加接近。
其中：

$V_c$ 决定了神经元的兴奋阈值。
$a_0$ 控制了神经元的发放频率和发放前膜电位的增长速度。
当膜电位达到峰值 $\theta$ 时，神经元发放动作电位，膜电位将被重置为 $V_{\text{reset}}$ 并进入不应期 $t_{\text{ref}}$ 。

2. QIF 模型的动力学性质

若不考虑不应期且 $\theta \to \infty, V_{\text{reset}} \to -\infty$ ，且外部电流输入 $I (t)$ 为常值 $I$ 的情况下，QIF 微分方程的通解为(笔者没有解出来，借鉴的相关资料)：
$\frac{V_{\text{rest}} + V_c}{2} + \sqrt{\frac{RI - \frac{a_0}{4}(V_{\text{rest}} - V_c)^2}{a_0}} \tan \left( \frac{t}{\tau} \sqrt{\left[ RI - \frac{a_0}{4}(V_{\text{rest}} - V_c)^2 \right] a_0} \right) \tag{3}$

该方程展示了 $V$ 对时间 $t$ 的变化为正切函数：

$\tan kt + n \tag{4}$

式中，

$\sqrt{\frac{RI - \frac{a_0}{4}(V_{\text{rest}} - V_c)^2}{a_0}}, \quad k = \frac{\sqrt{\left[ RI - \frac{a_0}{4}(V_{\text{rest}} - V_c)^2 \right] a_0}}{\tau}, \quad n = \frac{V_{\text{rest}} + V_c}{2} \tag{5}$

根据正切函数的周期性，QIF 模型的发放周期为

$\pi / k \tag{6}$

同时，为保证方程 (3) 中的根式有意义且不为 0（否则 $V$ 将不产生周期性变化），应要求

$\frac{a_0}{4}(V_{\text{rest}} - V_c)^2 > 0$ $\Rightarrow I > \frac{a_0}{4R}(V_{\text{rest}} - V_c)^2 \tag{7}$

对于基强度电流 $I_\theta$ 。当 $\leq I_{\theta}$ 时，神经元将不产生动作电位，且膜电位的稳定值随着电流的增加而增加；当电流超过基强度时神经元才能发放动作电位，且发放频率随电流的增加而增加。若 $I_{\theta}$ ，方程 (3) 右侧的第二项为 0，膜电位将稳定在 $\frac{V_{\text{rest}} + V_c}{2}$ 。

下面讨论一下 $a_0$ 与模型发放频率的关系。由方程 (6) 和方程 (5) 可知 QIF 模型的发放频率为

$\frac{k}{\pi} = \frac{\sqrt{-\frac{(V_{\text{rest}} - V_c)^2}{4a_0^2} + R I a_0}}{\pi \tau} \quad \tag{8}$

由方程 (7) 及 $a_0 > 0$ 可以求得 $a_0$ 的取值范围为 $a_0 \in \left(0, \frac{4RI}{(V_{\text{rest}} - V_c)^2}\right)$ 。由于方程 (8) 根式中的式子是关于 $a_0$ 的二次函数，根据二次函数性质， $f$ 在 $\left(0, \frac{2RI}{(V_{\text{rest}} - V_c)^2}\right)$ 内随 $a_0$ 单调递增，在 $\left(\frac{2RI}{(V_{\text{rest}} - V_c)^2}, \frac{4RI}{(V_{\text{rest}} -_c)^2}\right)$ 内随 $a_0$ 单调递减。

为什么一个恒定的外部电流输入 𝐼 要达到基强度后，QIF 模型才能产生动作电位呢？这部分可以可以利用 BrainPy里的一维相平面分析工具画出不同的恒定电流输入下膜电位变化率 d𝑉/d𝑡 与膜电位 𝑉 的关系。由于涉及到代码部分，因此相平面分析的部分放在代码的部分进行讨论。

3. $\theta$ 神经元模型

对于上述分析的式(1)，可以通过数学推导转换成更加简洁的形式。具体而言，将式(1)转化为如下的形式：
$\frac{dV}{dt} = \frac{a_0}{\tau} \left( V - \frac{V_{\text{rest}} + V_c}{2} \right)^2 + \frac{a_0}{\tau} \left[ V_{\text{rest}} V_c - \left( V - \frac{V_{\text{rest}} + V_c}{2} \right)^2 \right] + \frac{RI(t)}{\tau}\tag{9}$ 令 $\frac{a_0}{\tau} \left( V - \frac{V_{\text{rest}} + V_c}{2} \right)$ ，则有
$\frac{\tau}{a_0} \frac{dx}{dt} = x^2 + \frac{a_0}{\tau} \left[ V_{\text{rest}} V_c - \left( \frac{V_{\text{rest}} + V_c}{2} \right)^2 \right] + \frac{RI(t)}{\tau}$ $\Rightarrow \frac{dx}{dt} = x^2 + \frac{a_0}{\tau} \left( \frac{a_0}{\tau} \left[ V_{\text{rest}} V_c - \left( \frac{V_{\text{rest}} + V_c}{2} \right)^2 \right] + \frac{RI(t)}{\tau} \right)$ $\Rightarrow \frac{dx}{dt} = x^2 + bI(t) + c \quad \tag{10}$ 其中 $\frac{a_0 R}{\tau^2}$ ， $\frac{a_0^2}{\tau^2} \left( V_{\text{rest}} V_c \right) - \left( \frac{V_{\text{rest}} + V_c}{2} \right)^2$ 。令 $\frac{1}{2} \tan \theta$ ，代入上式，得到
$\frac{1}{2 \cos^2 \frac{\theta}{2}} \frac{d\theta}{dt} = \tan^2 \frac{\theta}{2} + bI(t) + c$ $\Rightarrow \frac{d\theta}{dt} = 2 \sin^2 \frac{\theta}{2} + 2 \cos^2 \frac{\theta}{2} (bI(t) + c)$ $\Rightarrow \frac{d\theta}{dt} = -\cos \theta + (1 + \cos \theta) \left( 2c + \frac{1}{2} + 2bI(t) \right) \quad \tag{11}$

这便是 $\theta$ 神经元模型（ $\theta$ -Neuron model）的一种数学表示，它和 $t_{\text{ref}} = 0$ , $\theta \to \infty$ , $V_{\text{reset}} \to -\infty$ 的 QIF 模型等价。
另一种经典表示与方程 (11) 大同小异：
$\frac{d\theta}{dt} = 1 - \cos \theta + (1 + \cos \theta) (\beta + I(t)) \quad \tag{12}$
理论分析可知：
和 QIF 模型相比，经过推导和简化后的 𝜃 神经元模型不再需要显式地重置发放脉冲的神经元，而是通过将 𝜃 限制在 (0, 2π) 的区间上隐式地完成这一操作。后面代码部分会进行详细的分析与说明。

4. 基于BrainPy 的 QIF 模型

下面利用 BrainPy 实现QIF模型，QIF 模型的定义与 LIF 模型相似，只需在初始化函数__init__()中初始化相应的参数，并修改微分方程的表达即可。代码如下：

import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt

plt.rcParams.update({"font.size": 15})
plt.rcParams['font.sans-serif'] = ['Times New Roman']


class QIF(bp.dyn.NeuDyn):
    def __init__(self, size, V_rest=-65., V_reset=-68., V_th=-0., V_c=-50.0, a_0=.07, R=1., tau=10., t_ref=5.,
                 **kwargs):
        # 初始化父类
        super(QIF, self).__init__(size=size, **kwargs)

        # 初始化参数
        self.V_rest = V_rest
        self.V_reset = V_reset
        self.V_th = V_th
        self.V_c = V_c
        self.a_0 = a_0
        self.R = R
        self.tau = tau
        self.t_ref = t_ref  # 不应期时长

        # 初始化变量
        self.V = bm.Variable(bm.random.randn(self.num) + V_reset)
        self.input = bm.Variable(bm.zeros(self.num))
        self.t_last_spike = bm.Variable(bm.ones(self.num) * -1e7)  # 上一次脉冲发放时间
        self.refractory = bm.Variable(
            bm.zeros(self.num, dtype=bool))  # 是否处于不应期
        self.spike = bm.Variable(bm.zeros(self.num, dtype=bool))  # 脉冲发放状态

        # 使用指数欧拉方法进行积分
        self.integral = bp.odeint(f=self.derivative, method='exp_auto')

    # 定义膜电位关于时间变化的微分方程
    def derivative(self, V, t, Iext):
        dvdt = (self.a_0 * (V - self.V_rest) *
                (V - self.V_c) + self.R * Iext) / self.tau
        return dvdt

    def update(self):
        _t, _dt = bp.share['t'], bp.share['dt']
        # 以数组的方式对神经元进行更新
        refractory = (_t - self.t_last_spike) <= self.t_ref  # 判断神经元是否处于不应期
        V = self.integral(self.V, _t, self.input, dt=_dt)  # 根据时间步长更新膜电位
        # 若处于不应期，则返回原始膜电位self.V，否则返回更新后的膜电位V
        V = bm.where(refractory, self.V, V)
        spike = V > self.V_th  # 将大于阈值的神经元标记为发放了脉冲
        self.spike.value = spike  # 更新神经元脉冲发放状态
        self.t_last_spike.value = bm.where(
            spike, _t, self.t_last_spike)  # 更新最后一次脉冲发放时间
        # 将发放了脉冲的神经元膜电位置为V_reset，其余不变
        self.V.value = bm.where(spike, self.V_reset, V)
        self.refractory.value = bm.logical_or(
            refractory, spike)  # 更新神经元是否处于不应期
        self.input[:] = 0.  # 重置外界输入

在定义好 QIF 模型后，简单地初始化一个 QIF 模型并进行模拟：

def run_QIF():
    # 运行QIF模型
    group = QIF(1)
    runner = bp.DSRunner(
        group, monitors=['V'], inputs=('input', 6.))  # 输入电流的变量和数值
    runner(500)  # 运行时长为500ms
    # 结果可视化
    fig, gs = bp.visualize.get_figure(1, 1, 4.5, 6)
    ax = fig.add_subplot(gs[0, 0])
    plt.plot(runner.mon.ts, runner.mon.V)
    plt.xlabel(r'$t$ (ms)')
    plt.ylabel(r'$V$ (mV)')
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    # plt.savefig('QIF_output2.pdf', transparent=True, dpi=500)
    plt.show()

得到的图像如下：
在恒定的电流输入下，QIF 模型的膜电位 𝑉 随时间 𝑡 的变化曲线
由上图可见，相比 LIF 模型，QIF 模型膜电位随时间变化的曲线和真实情况更加符合。尽管都是对 $V$ 重置的判断，式 (2) 中的 $\theta$ 和 LIF 模型中 $V_{\text{th}}$ 的含义不完全相同：在 LIF 模型中， $V$ 达到 $V_{\text{th}}$ 后开始发放脉冲（只不过整个动作电位的过程被简化为了重置），而在 QIF 模型中， $\theta$ 刻画的是脉冲发放过程中膜电位的尖峰值，动作电位在更早的时候就已经开始产生了。

对于上方代码中设定的各个参数，可以求得基强度电流为 $I_{\theta} = 3.94$ 。当 $I <= 3.94$ 时，模型将不产生动作电位。

下图给出了不同的恒定电流输入下膜电位随时间的变化。与 LIF 模型相似，当电流小于基强度时，神经元将不产生动作电位，且膜电位的稳定值随着电流的增加而增加；当电流超过基强度时神经元才能发放动作电位，且发放频率随电流的增加而增加。若 $I_{\theta}$ ，方程 (3) 右侧的第二项为 0，膜电位将稳定在 $\frac{V_{\text{rest}} + V_c}{2}$ 。
不同的恒定电流输入下膜电位 𝑉 随时间 𝑡 的变化
上述图片由下面的代码进行生成：

def QIF_input_threshold():
    def QIF_plot(input, duration, color):
        neu = QIF(1)
        neu.V[:] = bm.array([-68.])
        runner = bp.DSRunner(neu, monitors=['V'], inputs=('input', input))
        runner(duration)
        plt.plot(runner.mon.ts, runner.mon.V, color=color,
                 label='input={}'.format(input))

    inputs = [0., 3., 4., 5.]
    colors = [u'#2ca02c', u'#d62728', u'#1f77b4', u'#ff7f0e']
    dur = 500

    fig, gs = bp.visualize.get_figure(1, 1, 4.5, 6)
    ax = fig.add_subplot(gs[0, 0])
    for i in range(len(inputs)):
        QIF_plot(inputs[i], dur, colors[i])

    plt.text(104, -25, 'input=5.')
    plt.text(462, -25, 'input=4.')
    plt.annotate('input=3.', xy=(144, -61.5), xytext=(110, -45),
                 arrowprops=dict(arrowstyle="->"))
    plt.annotate('input=0.', xy=(237.5, -65.15), xytext=(215, -50),
                 arrowprops=dict(arrowstyle="->"))
    plt.xlabel(r'$t$ (ms)')
    plt.ylabel(r'$V$ (mV)')
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)
    plt.xlim(-1, 541)
    # 设置X轴的最小值为 -1，最大值为 541
    # plt.savefig('QIF_input_threshold.pdf', transparent=True, dpi=500)
    plt.show()

下面使用代码探讨 $a_0$ 与模型发放频率的关系

def a0_effect():
    duration = 500

    fig, gs = bp.visualize.get_figure(3, 1, 1.5, 6)

    neu1 = QIF(1, a_0=0.005)
    neu1.V[:] = bm.array([-68.])
    runner = bp.DSRunner(neu1, monitors=['V'], inputs=('input', 5.))
    runner(duration)
    ax1 = fig.add_subplot(gs[0, 0])
    ax1.plot(runner.mon.ts, runner.mon.V,
             color=u'#d62728', label=r'$a_0$=0.005')
    ax1.set_ylabel(r'$V$ (mV)')
    ax1.legend(loc='upper right')
    ax1.spines['top'].set_visible(False)
    ax1.spines['right'].set_visible(False)

    neu1 = QIF(1, a_0=0.045)
    neu1.V[:] = bm.array([-68.])
    runner = bp.DSRunner(neu1, monitors=['V'], inputs=('input', 5.))
    runner(duration)
    ax2 = fig.add_subplot(gs[1, 0])
    ax2.plot(runner.mon.ts, runner.mon.V,
             color=u'#1f77b4', label=r'$a_0$=0.045')
    ax2.set_ylabel(r'$V$ (mV)')
    ax2.legend(loc='upper right')  # 指定添加的图例的位置在右上角
    ax2.spines['top'].set_visible(False)
    ax2.spines['right'].set_visible(False)

    neu1 = QIF(1, a_0=0.08)
    neu1.V[:] = bm.array([-68.])
    runner = bp.DSRunner(neu1, monitors=['V'], inputs=('input', 5.))
    runner(duration)
    ax3 = fig.add_subplot(gs[2, 0])
    ax3.plot(runner.mon.ts, runner.mon.V,
             color=u'#ff7f0e', label=r'$a_0$=0.08')
    ax3.set_ylabel(r'$V$ (mV)')
    ax3.set_xlabel(r'$t$ (ms)')
    ax3.legend(loc='upper right')
    ax3.spines['top'].set_visible(False)
    ax3.spines['right'].set_visible(False)

    # plt.savefig('QIF_a0.png', transparent=True, dpi=500)
    plt.show()

在之前定义的 QIF 模型中，固定 $I = 5$ ，则 $a_0 \in (0, 0.089)$ 。图3.7展示了 $a_0$ 的取值对 QIF 神经元发放频率及发放曲线的影响。随着 $a_0$ 的增长，神经元发放频率先增加后降低。此外，随着 $a_0$ 的增长，阈下膜电位变化曲线从平滑上升变为先缓慢上升，后急速上升。因此， $a_0$ 不仅影响了 QIF 模型的发放频率，还刻画了膜电位的上升曲线。
𝑎0 的取值与 QIF 神经元膜电位随时间变化曲线的关系
实际上，在理论分析中， $a_0 = 0.045$ 时发放频率最大，但由于阈值电位和重置电位的存在，上图膜电位变化并没有经历一个完整的正切周期，因此发放频率达到最大值时 $a_0$ 并不严格等于 $\frac{2RI (V_{\text{rest}} - V_c)}{2}$ ，而是低于此值。

前面提到的一维相平面分析，在此使用BrainPy的相关工具进行可视化：

def phase_plane():
    bp.math.enable_x64()  # 启用64位浮点数计算模式

    def phase_plane_analysis(model, I_ext, res=0.005, extra_fun=None):
        fig, gs = bp.visualize.get_figure(1, 1, 3.5, 4.5)
        ax = fig.add_subplot(gs[0, 0])
        pp = bp.analysis.PhasePlane1D(
            model=model,
            target_vars={'V': [-80, -30]},
            pars_update={'Iext': I_ext},
            resolutions=res
        )
        pp.plot_vector_field()
        pp.plot_fixed_point()
        ax.set_xlabel(r'$V$')
        ax.spines['top'].set_visible(False)
        ax.spines['right'].set_visible(False)
        if extra_fun is not None:
            extra_fun()
        ax.get_legend().remove()
        # plt.savefig(f'QIF_I={I_ext}.pdf', dpi=500, transparent=True)

    qif = QIF(1)

    def f():
        plt.annotate('stable point', xy=(-65.0, 0),
                     xytext=(-73, 1.6), arrowprops=dict(arrowstyle="->"))
        plt.annotate('unstable point', xy=(-50.0, 0),
                     xytext=(-53, 1.6), arrowprops=dict(arrowstyle="->"))
        plt.scatter([-70, -45], [0., 0.], marker='4', s=100, color='k')
        plt.scatter([-58, ], [0., ], marker='3', s=100, color='k')
        plt.text(-30, 5, 'I=0.0', fontsize=25,
                 ha='right', va='top', color='purple')

    phase_plane_analysis(qif, 0., extra_fun=f)

    def f():
        plt.annotate('stable point', xy=(-63.977984, 0),
                     xytext=(-73, 1.6), arrowprops=dict(arrowstyle="->"))
        plt.annotate('unstable point', xy=(-51.022015, 0),
                     xytext=(-53, 1.6), arrowprops=dict(arrowstyle="->"))
        plt.scatter([-70, -45], [0., 0.], marker='4', s=100, color='k')
        plt.scatter([-58, ], [0., ], marker='3', s=100, color='k')
        # 右上角加上注释
        plt.text(-30, 5, 'I=1.0', fontsize=25,
                 ha='right', va='top', color='purple')

    phase_plane_analysis(qif, 1., extra_fun=f)

    def f():
        plt.annotate('stable point', xy=(-61.159625, 0),
                     xytext=(-70, 1.6), arrowprops=dict(arrowstyle="->"))
        plt.annotate('unstable point', xy=(-53.84037, 0),
                     xytext=(-55, 1.6), arrowprops=dict(arrowstyle="->"))
        plt.scatter([-70, -45], [0., 0.], marker='4', s=100, color='k')
        plt.scatter([-58, ], [0., ], marker='3', s=100, color='k')
        plt.text(-30, 5, 'I=3.0', fontsize=25,
                 ha='right', va='top', color='purple')

    phase_plane_analysis(qif, 3., extra_fun=f)

    def f():
        plt.scatter([-55], [0.], marker='4', s=100, color='k')
        plt.text(-30, 5, 'I=10.0', fontsize=25,
                 ha='right', va='top', color='purple')

    phase_plane_analysis(qif, 10., extra_fun=f)

    plt.show()

相平面分析结果下图所示。当 $I = 0.0$ 时， $\frac{dV}{dt}$ 有两个零点，即 $V_{\text{stable}} = V_{\text{rest}}$ 和 $V_{\text{unstable}} = V_c$ ，其中 $V_{\text{stable}}$ 为稳定点（图中“stable point”）， $V_{\text{unstable}}$ 为不稳定点（图中“unstable point”）。此时，该模型表现出初始点依赖特性。

当初始膜电位 $V(0) < V_c$ 时，膜电位会逐渐被稳定点所吸引（如图 $I = 0.0$ 中箭头所示），直至稳定到 $V_{\text{rest}}$ ；
当初始膜电位 $V(0) > V_c$ 时， $V$ 受到不稳定的排斥会不断升高（如图 $I = 0.0$ 中箭头所示），直至产生动作电位发放。

当给予神经元一定电流时，此时模型的相图将发生变化。如图 $I = 1.0$ 、图 $I = 3.0$ 和图 $I = 10.0$ 所示， $d V / d t$ 随着 $I$ 的增大而上移。上移过程中，两个不动点逐渐靠近（图 $I = 3.0$ ），并合并为一个鞍点（saddle point），直至最终消失（图 $I = 10.0$ ）。在动力学系统理论中，我们一般将此过程称为鞍结分岔（saddle-node bifurcation）。
若神经元接受到一个 $I_\theta$ 的恒定电流输入时（图3.8（b）），模型有两个不动点。我们令方程 (3.11) 左侧等于 0，可以求得膜电位的这两个不动点为
$V_{stable} = \frac{V_{rest} + V_c}{2} - \frac{1}{2}\sqrt{(V_{rest} + V_c)^2 - \frac{4RI}{a_0}}\tag{13}$ $V_{unstable} = \frac{V_{rest} + V_c}{2} + \frac{1}{2}\sqrt{(V_{rest} + V_c)^2 - \frac{4RI}{a_0}}\tag{14}$

当 $I_\theta$ 时（图 $I = 10.0$ ），外部电流输入将 $d V / d t$ 全部提高到了 x 轴以上，因此膜电位一直上升，直到动作电位被激发。

经过上面的讨论，我们可以发现，QIF 模型中的 $V_{unstable}$ 与 LIF 模型中 $V_{th}$ 的含义更加相似，膜电位在越过这一阈值后就开始产生脉冲，其变化也变得不可逆。但与 LIF 模型不同的是，使得 QIF 神经元兴奋的膜电位阈值并不是一个恒定值。当膜电位越过不稳定点时，膜电位将持续上升直至达到阈值，而不稳定点会随着外部电流的输入而改变。当外部电流输入增大时，不稳定点左移（见图 $I = 0.0$ 和 $I = 3.0$ ）。

if __name__ == '__main__':
    pass
    run_QIF()
    QIF_input_threshold()
    a0_effect()
    phase_plane()

下面使用BrainPy根据方程 (11) 构建一个 𝜃 神经元模型：

import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt

plt.rcParams.update({"font.size": 15})
plt.rcParams['font.sans-serif'] = ['Times New Roman']


class Theta(bp.dyn.NeuDyn):
    def __init__(self, size, b=0., c=0., t_ref=0., **kwargs):
        # 初始化父类
        super(Theta, self).__init__(size=size, **kwargs)

        # 初始化参数
        self.b = b
        self.c = c
        self.t_ref = t_ref

        # 初始化变量
        self.theta = bm.Variable(bm.random.randn(self.num) * bm.pi / 18)
        self.input = bm.Variable(bm.zeros(self.num))
        self.spike = bm.Variable(bm.zeros(self.num, dtype=bool))  # 脉冲发放状态

        # 使用指数欧拉方法进行积分
        self.integral = bp.odeint(
            f=self.derivative, method='exponential_euler')

    # 定义膜电位关于时间变化的微分方程
    def derivative(self, theta, t, I_ext):
        dthetadt = 1-bm.cos(theta) + (1. + bm.cos(theta)) * \
            (2 * self.c + 1 / 2 + 2 * self.b * I_ext)
        return dthetadt

    def update(self):
        _t, _dt = bp.share['t'], bp.share['dt']
        # 以数组的方式对神经元进行更新
        theta = self.integral(self.theta, _t, self.input, dt=_dt) % (
            2 * bm.pi)  # 根据时间步长更新theta
        # 将theta从2*pi跳跃到0的神经元标记为发放了脉冲
        spike = (theta < bm.pi) & (self.theta > bm.pi)
        self.spike[:] = spike  # 更新神经元脉冲发放状态
        self.theta[:] = theta
        self.input[:] = 0.  # 重置外界输入

并可以根据 QIF 模型的参数计算 𝜃 神经元模型的参数，以此创建模型并运行仿真模拟：

# 根据QIF模型的参数计算theta神经元模型的参数
V_rest, R, tau, t_ref = -65., 1., 10., 5.
a_0, V_c = .07, -50.0
b = a_0 * R / tau ** 2
c = a_0 ** 2 / tau ** 2 * (V_rest * V_c - ((V_rest + V_c) / 2) ** 2)

# 运行theta神经元模型
neu = Theta(1, b=b, c=c, t_ref=t_ref)
runner = bp.DSRunner(neu, monitors=['theta'], inputs=('input', 6.))
runner(50)

# 可视化

fig, gs = bp.visualize.get_figure(1, 1, 4.5, 6)
ax1 = fig.add_subplot(gs[0, 0])
ax1.plot(runner.mon.ts, runner.mon.theta)
ax1.set_xlabel(r'$t$ (ms)')
ax1.set_ylabel(r'$\Theta$')
ax1.spines['top'].set_visible(False)
ax1.spines['right'].set_visible(False)
# plt.savefig('theta_neuron_time_evolution.pdf', transparent=True, dpi=500)

fig, gs = bp.visualize.get_figure(1, 1, 4.5, 6)
ax2 = fig.add_subplot(gs[0, 0])
ax2.plot(bm.cos(runner.mon.theta), bm.sin(runner.mon.theta))
ax2.set_xlabel(r'$\cos(\Theta)$')
ax2.set_ylabel(r'$\sin(\Theta)$')
ax2.spines['top'].set_visible(False)
ax2.spines['right'].set_visible(False)
# plt.savefig('theta_neuron_phase.pdf', transparent=True, dpi=500)
plt.show()

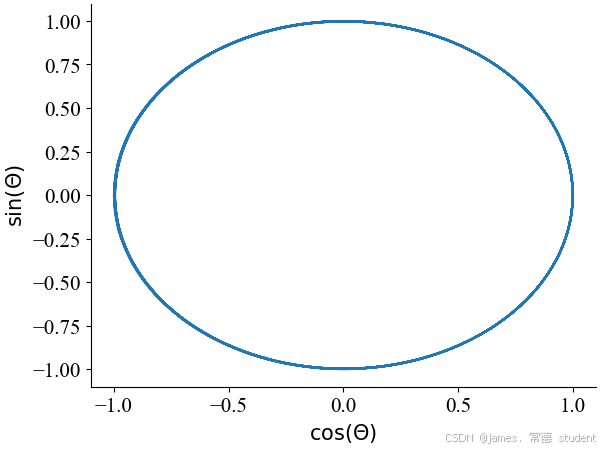
上述两张图均是在 $\theta$ 神经元在接收到强度为 6 的输入时的变化，其中左图展示了 $\theta$ 随时间的演化，右图展示了 $\sin (\theta)$ 和 $\cos (\theta)$ 的相图关系。

和 QIF 模型相比，经过推导和简化后的 $\theta$ 神经元模型不再需要显式地重置发放脉冲的神经元，而是通过将 $\theta$ 限制在 $2\pi)$ 的区间上隐式地完成这一操作（如左图所示）。观察仿真过程中 $(\sin \theta, \cos \theta)$ 的值，则可以将 $\theta$ 在 $2\pi)$ 的变化视作一个圆周运动，每当 $\theta$ 到达 $2\pi$ 处，神经元便会被“重置”到 0 位置，从而使 $\theta$ 的连续性不被破坏（如右图所示）。