Codeforces Round #841 (Div. 2) A-D

Codeforces Round #841 (Div. 2)

比赛网址

A. Joey Takes Money

题目大意

给你一个数列 $a_n=a_1,a_2,a_3,\dots ,a_n$

每次你可以选择数列中的两个数 $a_j$ , $a_k$ ， 并自己选择两个数 $x$ , $y$

但是要满足条件$a_j\cdot a_k=x\cdot y$ ，然后你可以用 $x$ ，$y$ 来替换 $a_j$ , $a_k$

以上操作可以进行无数次，你需要使最后数组的和最大

注意输出时要将答案乘上2022

思路/证明

第一直觉是：在给定 $x\cdot y=k$ 的情况下，只有让一个数等于 $1$ 才能让 $x+y$ 达到最大

证明如下：

已知 $a_j\cdot a_k=x\cdot y$ , $那么:y=\frac{a_j\cdot a_k}{x}$

所以 $x+y=x+\frac{a_j\cdot a_k}{x}=F(x)$

$a_j$ , $a_k$ 为定值，所以F(x)实际上是一个对勾函数

$x\ge 1,y\ge 1$ ,所以 $x$ 的范围实际上是$[1,a_j\cdot a_k]$

对勾函数的最小值包含在此区间内，所以我们对两个端点求值，然后判断大小，最大的即为两数相乘的最大值

当 $x=1$ 时， $F(x)=a_j\cdot a_k$ , 当$x=a_j\cdot a_k$ 时，$F(x)=a_j\cdot a_k$

所以当 $x=1$ , $y=a_j\cdot a_k$ 时， $x+y$ 达到最大

所以 ：在给定 $x\cdot y=k$ 的情况下，只有让一个数等于 $1$ 才能让 $x+y$ 达到最大

所以这个数组最后的情况是：$a_n^{\prime }=1,1,1,\dots ,{\prod }_{i=1}^n{a}_i$

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
lli total_ask, total_num;
signed main()
{
    ios::sync_with_stdio(false),cin.tie(0), cout.tie(0);
    cin >> total_ask;
    for(int temp = 0 ; temp < total_ask ; temp++){
        lli ans = 1, put;
        cin >> total_num;
        for(int temp2 = 0 ; temp2 < total_num ; temp2++){
            cin >> put;
            ans *= put;
        }
        ans += total_num - 1;
        cout << ans*2022 << "\n";
    }
    return 0;
}

B. Kill Demodogs

题目大意

有一个 长度为 $n$ 的矩阵，每个点$(i,j)$ 的权值为 $i\cdot j$

需要从$(1,1)$ 前往 $(n,n)$ ， 途中将路过的权值相加，注意要加上 开头和结尾即：$(1,1)$ , $(n,n)$

将结果乘于 2022 并 mod $(10^9+7)$

思路/证明

由图可知，虚线左右两边的值是关于虚线对称的

所以我们可以吧下半部分舍去，只参考上半部分

我们观察在同一列时值的情况

在点 $(i,j),i\in [1,j]$ 上，起权值 $ v = i \cdot j$ ，可以观察到， 当$i=j$的时候权值达到最大

又因为人物只能向右或向下行走，不能斜线走，所以我们采用之字形走法，这样可以尽可能的接近对角线

所以最大权值和为
$$V_{sum}=\sum _{i=1}^{n}i\cdot i+\sum _{i=1}^{n-1}i\cdot (i+1)$$
这两个求和实际上可以化简：
$$\begin{array}{rl}& \sum _{i=1}^n{n}^2的前n项和为S_n=\frac{n(n+1)(2n+1)}{6}\\ & 证明如下:\\ & (n-1{)}^3-n^3=(n^3+3n^2+3n+1)-n^3=3n^2+3n+1\\ & 依次枚举\\ & 2^3-1^3=3\times 1^2+3\times 1+1\\ & 3^3-2^3=3\times 2^2+3\times 2+1\\ & \dots \dots \dots \dots \\ & (n-1{)}^3-n^3=3n^2+3n+1\\ & 将上述式子相加，得:\\ & (n-1{)}^3-1=3\times [1^2+2^2+3^2+\cdots +n^2]+3\times [1+2+3+\cdots +n]+n\\ & (n-1{)}^3-1=3\times S_n+3\times \frac{n(n+1)}{2}+n\\ & 化简得:S_n=\frac{n(n+1)(2n+1)}{6}\\ & 所以可以得出:\\ & \sum _{i=1}^{n}i\cdot i+\sum _{i=1}^{n-1}i\cdot (i+1)=S_n+S_{n-1}+\frac{n(n-1)}{2}\\ & 化简得:\\ & \sum _{i=1}^{n}i\cdot i+\sum _{i=1}^{n-1}i\cdot (i+1)=\frac{n(n+1)(4n-1)}{6}\end{array}$$
最后不要忘记乘上2022，我们可以在我们推出得结论上乘上2022，即：
$$ans=\frac{n(n+1)(4n-1)}{6}\cdot 2022=337n(n+1)(4n-1)(mod10^9+7)$$

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
lli put, total_ask;
lli mod(lli number){
    return number % (1000000007);
}
signed main()
{
    cin >> total_ask;
    for(lli temp = 0 ; temp < total_ask ; temp++){
        cin >> put;
        lli ans = mod(337*mod(mod(put*(put+1))*(4*put - 1)));
        cout << ans << "\n";
    }
    return 0;
}

C. Even Subarrays

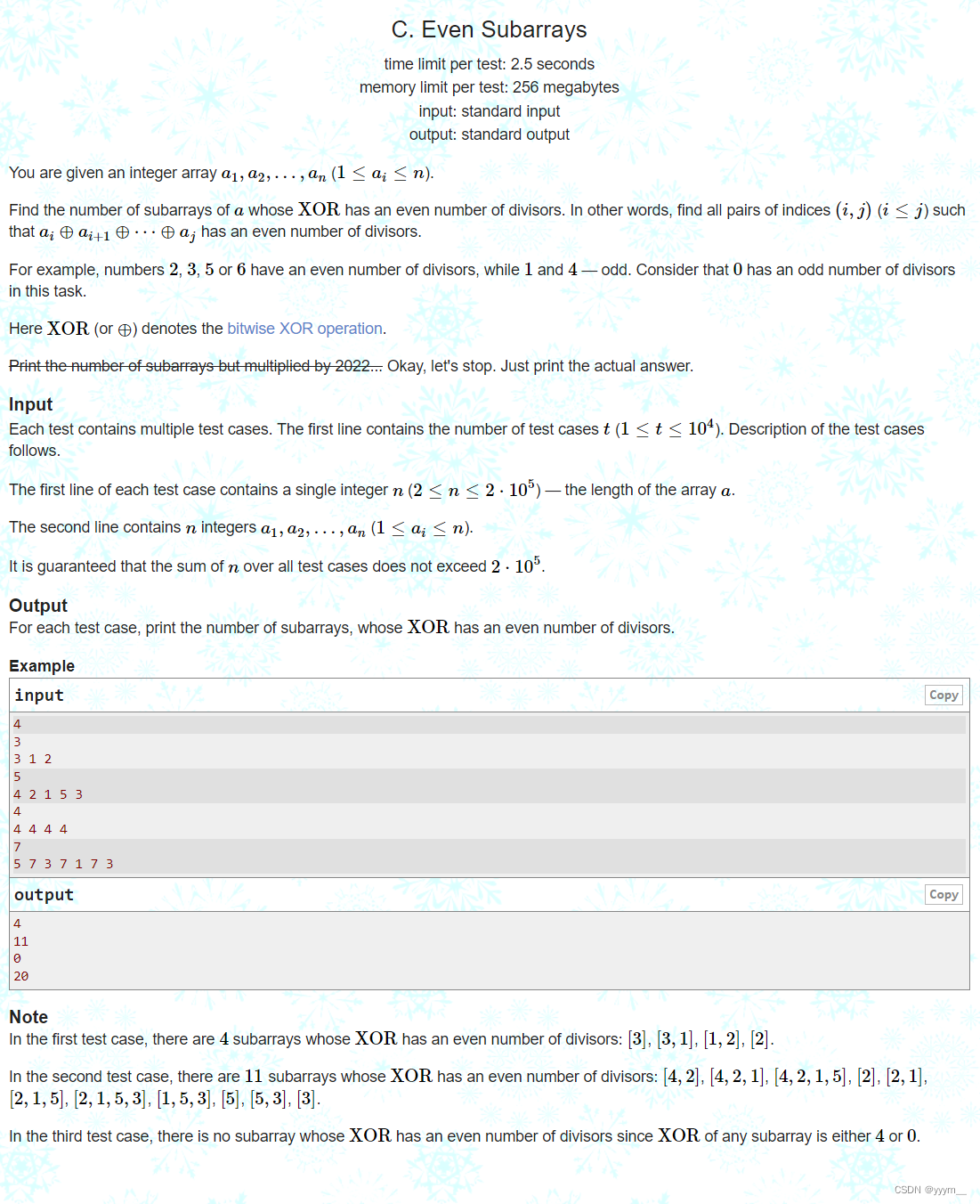
题目大意

给你一个数列$a_n=a_1,a_2,\dots ,a_n$

问有多少个区间的异或和有偶数个除数

思路/证明

首先我们要明确，什么样的数有偶数个除数，或者说什么样的数有奇数个除数

假设我们现在有一个数 $a$ ，有一个除数为$i$ ，那么可以知道的是另一个除数为 $\frac{a}{i}$

这样我们会发现只要存在一个除数，那么必然有另外一个除数与其相对

那什么时候会只有一个呢 ， 即 $i=\frac{a}{i}$ ， 换句话说，这个数是完全平方数

解决完第一个问题，那我们考虑一下区间异或和以及异或的相关性质

异或是用来判断两个数是否相等，但这不重要，重要的是如果一个数被相同的数异或两个，那么结果是它本身

即： $a^{\wedge }b=c{c}^{\wedge }b⟺a^{\wedge }{b}^{\wedge }b=a$

接下来就是区间问题了

区间求和一般是用前缀和， 在这里也可以使用前缀和，[a,b]^[a,c] = [b,c]

另外我们可以采取另一种方法来确定有多少种区间和

如果在预处理完前缀和后再一个一个枚举的话会超时

我们是已经可以知道总共的区间和的，即$\frac{(1+n)n}{2}$ ，因为枚举的次数是等差数列

所以我们可以算出不符合条件的区间个数，然后相减即可

求出来有多少个左边界使得这个区间的异或和为完全平方数就行了

已知$a^{\wedge }b=c$ ,那么 $a^{\wedge }c=b$ ， c即是平方数，这个平方数我们是可以枚举出来的

另外值得注意的是 ：memset()不能随便用，会超时

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long int lli;
const lli N = 3*1e5;
lli arr[N], Find[3*N];//Find用来存储前缀和为i的区间有多少个
lli total_ask, total_num, ans=0;
signed main()
{
    ios::sync_with_stdio(false),cin.tie(0), cout.tie(0);
    cin >> total_ask;
    while(total_ask--){
        cin >> total_num;
        lli wc = 2*total_num; //wc为异或和所能达到的最大值
        for(lli temp = 0 ; temp <= wc ; temp++) Find[temp] = 0;
        Find[0]++;
        lli ans = 0;
        for(int temp = 1 ; temp <= total_num ; temp++){
            lli number;
            cin >> number;
            arr[temp] = arr[temp - 1]^number;
            for(int temp2 = 0 ; temp2*temp2 <= wc ; temp2++) //枚举出所有可能出现的平方数
                ans += Find[arr[temp]^(temp2*temp2)];
            Find[arr[temp]]++;
        }
        cout << ((1+total_num)*total_num)/2 - ans << "\n";
    }
    return 0;
}

D. Valiant’s New Map

题目大意

有一个长宽分别为 $n$ , $m$ 的地图，地图上的每个点$(i,j)$ 都被一栋高 $h$ 的楼占据

存在一个$l\times l$ 的区间， 区间内的楼高度均大于 $l$

问最大的 $l$ 是多少

思路/证明

首先可以想到： 假设边长为 $i$ 的时候成立，那么边长小于 $i$ 的时候也一定成立，可能存在大于$i$的情况成立

这可以让我们联想到二分法， 如果当前边长可以，那么就继续二分大于$i$的部分

接下来就是如何判断是否存在边长为i的区域存在了

我们可以使用二维前缀和，将高度大于等于 $i$ 的点值设为1，小于 $i$ 的点的值设为0

如果该区域的和等于 边长乘边长，则存在

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 10000;
typedef long long int lli;
lli total_ask, vertical, level, number;
bool Check(lli num, vector<vector<lli>> origin){
    vector<vector<int>>div_(vertical + 1, vector<int>(level + 1));
    for(int temp = 1 ; temp <= vertical ; temp++){
        for(int temp2 = 1 ;temp2 <= level ; temp2++){
            lli tem = div_[temp - 1][temp2] + div_[temp][temp2 - 1] - div_[temp-1][temp2-1];
            if(origin[temp][temp2] >= num)
                div_[temp][temp2] = tem+1;
            else
                div_[temp][temp2] = tem;
        }
    }
    for(int temp = num ; temp <= vertical ; temp++){
        for(int temp2 = num ; temp2 <= level ; temp2++){
            lli one = div_[temp - num][temp2];
            lli two = div_[temp][temp2 - num];
            lli there = div_[temp - num][temp2 - num];
            lli Judge = div_[temp][temp2] - one - two + there;
            if(Judge == num*num)
                return 1;
        }
    }
    return 0;
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> total_ask;
    while(total_ask--){
        cin >> vertical >> level;
        vector<vector<lli>> origin(vertical + 1, vector<lli>(level + 1));
        for(int temp = 1 ; temp <= vertical ; temp++){
            for(int temp2 = 1 ; temp2 <= level ; temp2++)
                cin >> origin[temp][temp2];
        }
        lli left = 1, right = min(vertical, level) + 1;
        while(left < right){
            lli mid = (left + right) >> 1;
            if(Check(mid, origin)) left = mid+1;
            else right = mid;
        }
        cout << left-1 << "\n";
    }
    return 0;
}

注：E F 以后再说…
毕竟我也不会（指拉格朗日插值法）