深度剖析C语言的数据存储过程

数据存储

1. 深度剖析数据在内存中的存储

1.1数据类型的详细介绍

类型的意义：

1. 使用这个类型开辟内存空间的大小（大小决定了范围）。
2. 如何看待内存的视角

整形家族

为什么char也是整形：字符的本质是ASCII码值，是整形所以划分到整形家族。

构造类型：自定义类型-我们可以自己创建出来的类型

浮点型：

指针类型：

 

空类型：void

1. 整形在内存中的存储

我们之前讲过一个变量的创建是要在内存中开辟空间。空间的大小是根据不同的类型决定的。

那接下来我们谈谈数据在所开辟内存中到底如何存储的？

整数的二进制的表示形势有三种形式

1. 正的整数，源码，反码，补码相同
2. 负的整数，原码，反码，补码，是需要计算的
3. 原码：直接通过正负的形势写出的二进制序列就是原码

   反码：原码的符号位不变，其他位按位取反得到的就是反码

   补码：反码+1就是补码

正数：

负数：

二进制转化为十六进制

数据的存储方式：

得出结论：数据的存储是补码（只要是整数）

 

好处：补码可以实现加法与减法的互换

列如：1+（-1）

原码计算

无法得到真确结果

补码计算

计算的简便方法

补码倒着存的原因：存在大端与小端

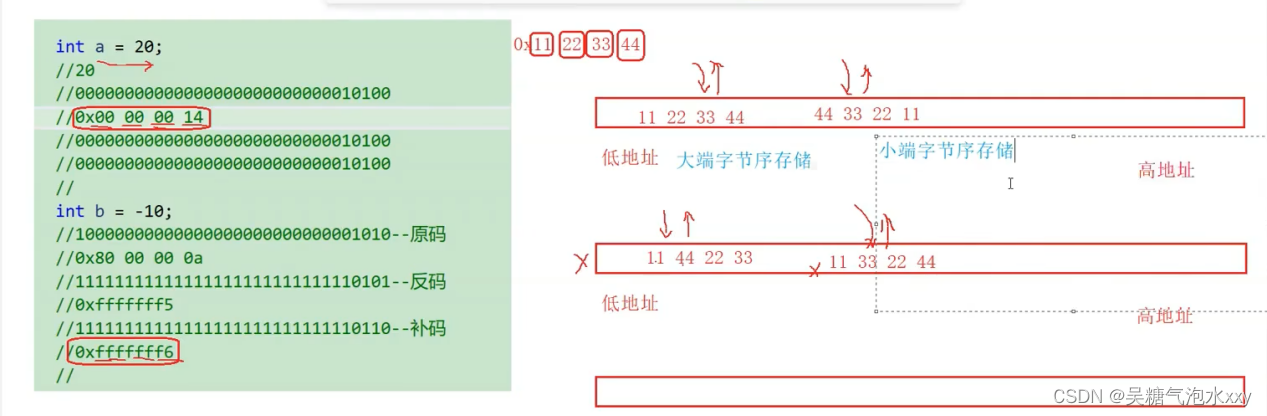
大端（小端）字节序的理解：

大端字节序存储：

把一个数据的高位字节序的内容放在低地址处，把低位字节序的内容放在高位地址处，就是大端字节序存储。

小端字节序存储：

把一个数据的高位字节序的内容放在高地址处，把低位字节序的内容放在低位地址处，就是小端字节序存储。

为什么会有大小端呢？

代码：大端小端的字节序检验

中心思想：使用指针来解引用找到第二个数的大小。

 

拿出的第一个字节的地址如果是01则是大端，00则是小端。

 

数据存储的实战：

输出 a=-1  b=-1  c=255

计算原理：因为无符号char的范围是  0~255不能放入-1

关键点拨：char a是一个字节只能存放八个比特位

%d是打印有符号的整形------需要整形提升

有符号高位补一      11111111111111111111111111111-----内存中的补码

a                       1000000000000000000000000000----- 内存中的反码

                         1000000000000000000000000001------内存中的原码--=  -1

                        

C  -1的原码    10000000000000000000000000001 

         反码      11111111111111111111111111110

         补码      11111111111111111111111111111------放入c中

            

但由于c是char类型需要截断 截断后的c ----11111111

无符号高位补0  0000000000000000000011111111-----内存中的补码   ==255

截断  把int放入short中需要16个比特位

      把int放入char中需要8个比特位

解释如下

补码————原码  取反加一

代码2

%u 打印无符号整数  u=unsigned无符号

Char范围-128~127

//100000000000000000000010000000----原码

 1111111111111111111111101111111----反码

 1111111111111111111111111100000---补码

发生截断得到 a=10000000    整形提升高位补1

111111111111111111110000000--提升

无符号数没有原反补的概念

所以直接打印的结果是4294967168

Printf（“%d\n”,a）;

%d打印有符号数

1111111111111111111110000000----补码

1000000000000000000001111111----反码

1000000000000000000010000000---原码   结果是-128

 代码3

-20的原码 10000000000000000000000000010100

     反码 11111111111111111111111111101011

     补码 11111111111111111111111111101100

无符号 unsigned int j=10   原反补相同

       00000000000000000000000000000001010

i+j   补码相加减    111111111111111111111111111101100

                   000000000000000000000000000001010

                   111111111111111111111111111110110--补码  但打印的是%d有符号所以取原码

                   100000000000000000000000000001001--反码

                   100000000000000000000000000001010-原码------   -10

      结果输出-10

   

 代码4

过程解析：0-1=-1

-1的原码   100000000000000000000000000000000001

反码   111111111111111111111111111111111110

补码   111111111111111111111111111111111111=4294967292

因为 unsigned为无符号数  原码与补码相同

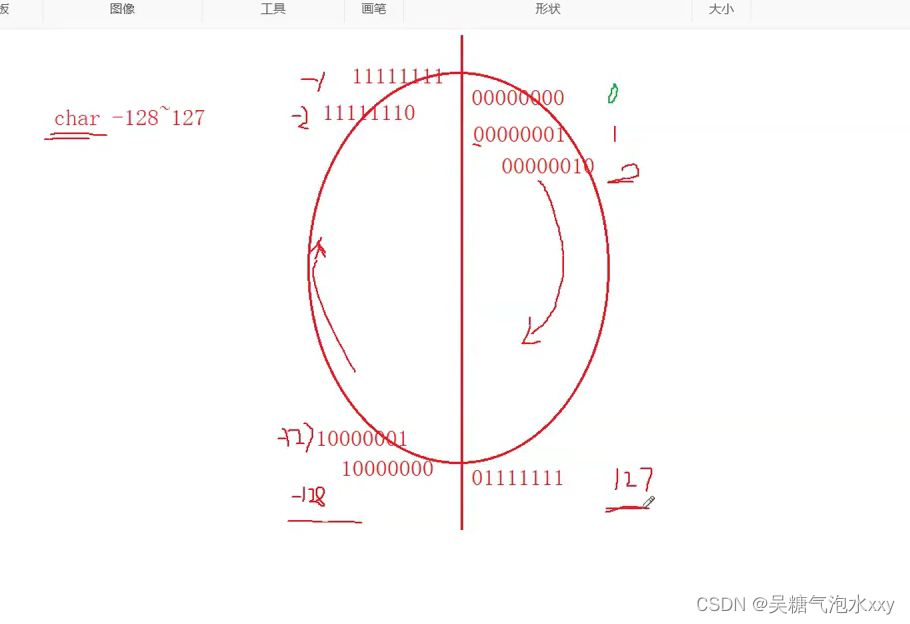
代码5

      \0的阿SKII码为0，则在0之前有多少个字符   128+127=255

浮点型在数据中的存储

常见的浮点数

3.1415926

1E10=1.0乘以10的10次方

浮点型的家族类型包括：float   double  longdouble

浮点数的表示的范围：float中定义

一个列子

说明：整形与浮点型的存储方式不一样。

 浮点数的存储规则

Num和*pfloat在内存中明明是一个数，为什么浮点数和整数的解读结果会差别这么大？

要理解结果，一定要搞清楚浮点数在计算机内部的表示方法。

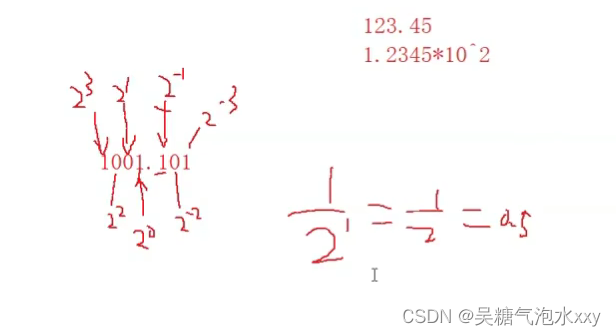
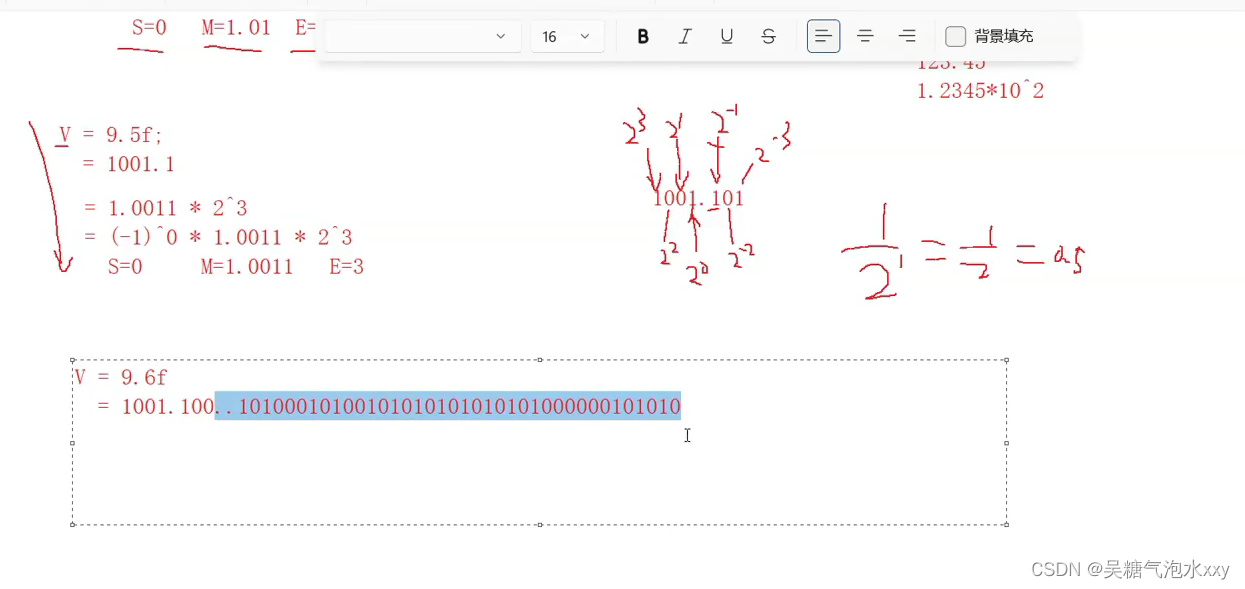
关键点拨：是二进制

IEEE 745规定：

对于32位的浮点数，最高的1位是符号s位，接着的8位是指数E,剩下的23位位有效数字M.

对于m

对于e

 举个例子5.5

代码如下

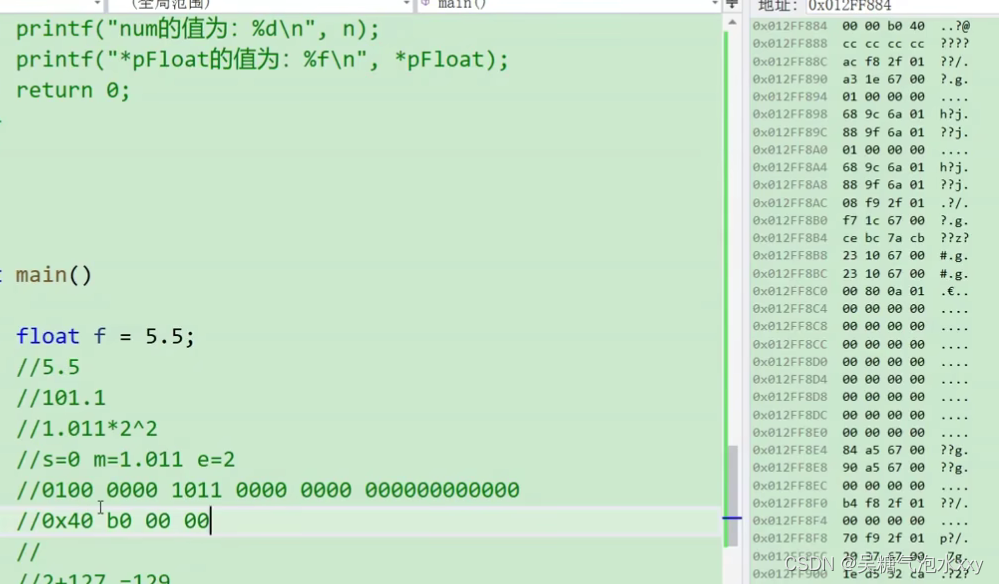
由于存在大小端的问题所以会倒着存

如何把存储的取出来？

  指数E从内存中取出还可以分成三种情况：

1. E不全为0或不全为1

1. E全为0

1. E为全1

举个例子

分析如下：

1. 原反补相同 000000000000000000000001001

   还原过程 浮点数

            0 0000000000 0000000000001001

            E=-126 ------E为全0

            M=0.00000000000000000001001

            结果为:M*2的E次方

完结。