洛谷 P1631 序列合并（详解）c++

题目链接：P1631 序列合并 - 洛谷 | 计算机科学教育新生态

1.题目解析

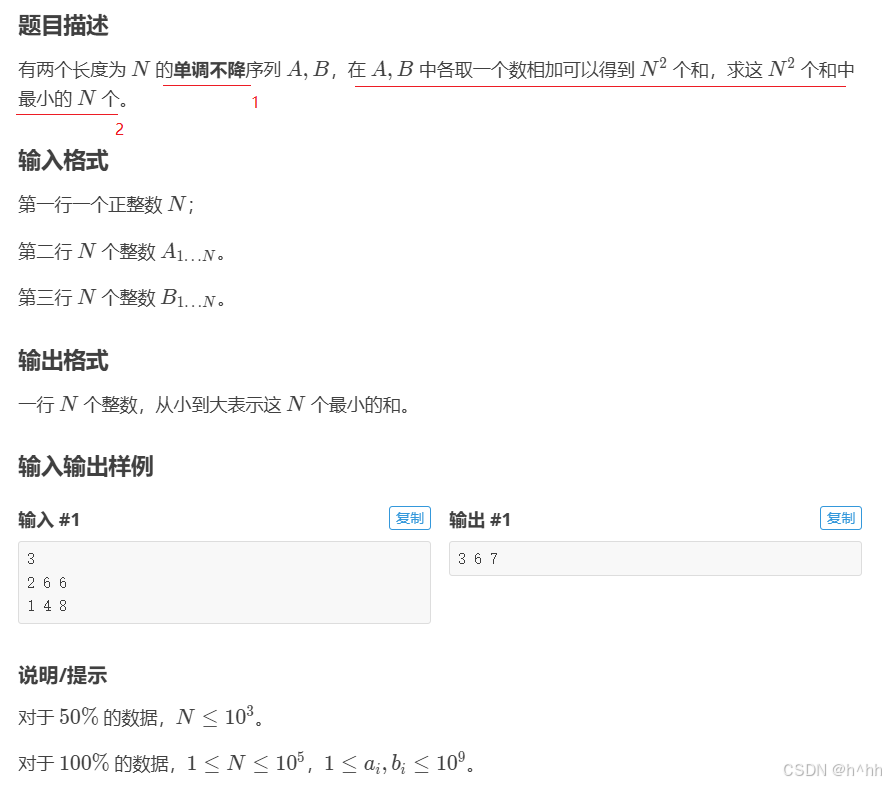
1：单调不降的意思是增的时候有可能水平然后再增再水平再增，但整体呈现一个上升趋势

2：图解

                      

2.算法原理

解法一：暴力求解
把所有的和全部算出来，然后找出最小的n个
行不通，数据范围是10的五次方，把所有的合算出来就是N的2次方，肯定会超时

解法二：利用单调性
先把 a[i] + b[1] 的所有值计算出来，放进小根堆中，拿出堆顶元素（最小的值），把下一个和计算出来，在方入堆中；堆里面存<和，a的编号，b的编号>，比如刚开始把 <3,1,1> <6,2,1> <6,3,1> 放入堆中

我们来找找规律，题目告诉我们ab都是单调递增的；当a里面的2，和b里面的1 4 8相加时，呈现单调上升的趋势，因为左边的数不变，右边的数依次增加，整体的趋势就是单调递增的，同理a里面的另外两个数也是如此，2+1算出来等于3的时候，如果这个数还没有被统计到最终的结果中，下面2+4算出来的6必定不可能是最终的结果，因为3 6 10是依次递增的，较小的数还没有放在最终的结果中，6和10根本就没有算出来的必要，后面同理，因此刚开始的时候仅需算出来第一行就足够了，因为第一行才有可能是最终的答案，当拿出来第一行最小的数的时候，接下来再把下一个数算出来就可以了，比如第一行最先拿出来3，再去考虑6，6放进来之后再考虑7

代码：

#include <iostream>
#include <queue>

using namespace std;

const int N = 1e5 + 10;

int n;
int a[N], b[N];

struct node {
	int sum; //和
	int i, j; //a和b的下标

	bool operator <(const node& x) const
	{
		//小根堆
		return sum > x.sum;
	}
};

priority_queue<node> heap;

int main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i) cin >> a[i];
	for (int i = 1; i <= n; ++i) cin >> b[i];

	//1.将a[i] + b[1]放进堆里
	for (int i = 1; i <= n; ++i) heap.push({ a[i] + b[1], i, 1 });

	//2.依此拿出n个数
	for (int k = 1; k <= n; ++k)
	{
		node t = heap.top(); heap.pop();
		int sum = t.sum, i = t.i, j = t.j;
		cout << sum << " ";
		//j+1有可能越界
		if (j + 1 <= n) heap.push({ a[i] + b[j + 1], i, j + 1 });
	}

	return 0;
}