二叉搜索树
二叉搜索树概念
二叉搜索树又称二叉排序树/二叉查找树,它可以是空树/具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
二叉搜索树操作
1. 二叉搜索树的查找
a 从根开始比较,比根大则往右边走,比根小则往左边走
b 走到到空,还没找到,则这个值不存在
2. 二叉搜索树的插入
a 树为空,则直接新增节点,赋值给root指针,成为根节点
b 树不空,按二叉搜索树性质查找插入位置,插入新节点
3 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,若不存在,则返回,若存在,则有以下情况:
a 要删除的结点无孩子结点
b 要删除的结点只有左孩子结点
c 要删除的结点只有右孩子结点
d 要删除的结点有左、右孩子结点
其中a可以归并到b,c中,所以实际上真正的情况只有三种:
b的解决方案:(直接删除法)删除该结点且使被删除节点的父结点指向被删除节点的左孩子
c的解决方案:(直接删除法)删除该结点且使被删除节点的父结点指向被删除结点的右孩子
d的解决方案:(替换法)找出右子树的最小节点,将它与被删除节点的值替换,再处理删除问题

若是删除7和14,则是直接删除法
若是删除3,则是替换法

二叉搜索树的实现
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K&key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool Insert(const K& key)
{
if (_root == nullptr)//第一次插入
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);//新节点
if (parent->_key < key)//链接
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else//找到了,开始删除
{
if (cur->_left == nullptr)//被删除节点只有右孩子
{
if (cur == _root)//若是当前被删除节点位根
{
_root = cur->_right;
}
else//删除的不是根节点
{
if (cur == parent->_left)//被删除节点在父节点的左边
{
parent->_left = cur->_right;//它的父节点接管它的右孩子
}
else//被删除节点在父节点的右边
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)//被删除节点只有左孩子
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else//被删除节点左右孩子都有(替换法)
{
Node* parent = cur;
Node* subLeft = cur->_right;
while (subLeft->_left)//找到右子树的最小节点(最左节点)
{
parent = subLeft;
subLeft = subLeft->_left;
}
swap(subLeft->_key, cur->_key);
if (subLeft == parent->_left)//最左节点在左边
{
parent->_left = subLeft->_right;
}
else//最左节点在右边(当右子树的根节点就是右子树的最小节点时)
{
parent->_right = subLeft->_right;
}
delete subLeft;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool FindR(const K& key)//递归版本(需要封装一层,因为需要传入_root)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)//递归版本
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)//递归版本
{
return _EraseR(_root, key);
}
private:
bool _EraseR(Node* &root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else//找到了,开始删除
{
if (root->_left == nullptr)//被删除节点只有右孩子
{
Node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)//被删除节点只有左孩子
{
Node* del = root;
root = root->_left;
delete del;
return true;
}
else//被删除节点有左右孩子
{
Node* subLeft = root->_right;//找右子树中的最小节点
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
swap(subLeft->_key, root->_key);
return _EraseR(root->_right, key);
}
}
}
bool _InsertR(Node* &root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};测试:
int main()
{
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
BSTree<int> bt;
for (auto e : a)
{
bt.Insert(e);
}
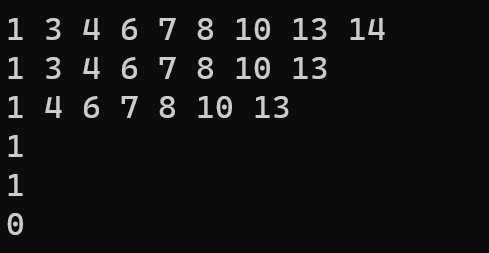
bt.InOrder();
bt.EraseR(14);
bt.InOrder();
bt.Erase(3);
bt.InOrder();
cout << bt.Find(1) << endl << bt.FindR(13) << endl << bt.Find(18) << endl;
return 0;
}
二叉搜索树的应用
1 Key的搜索模型(K模型):只有key作为关键码,结构中只需要存储Key
用于确定一个值(Key)在不在,如门禁系统都是Key的搜索模型
2 Key/Value的搜索模型(KV模型)):
每一个关键码key,都有与之对应的值Value,即<Key,Value>的键值对
a 可以确定Key在不在
b 通过Key查找Value
如英汉字典(通过英文可以快速找到对应的中文)英文与对应中文即构成键值对
如统计单词出现的次数(统计成功后,给定单词就可快速找到其出现的次数)
单词与其出现次数即构成键值对
k模型与kv模型的代码实现基于二叉搜索树的代码实现,区别不大,只是kv模型需要存储key和value
K模型的代码实现:
namespace key
{
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
Node* parent = cur;
Node* subLeft = cur->_right;
while (subLeft->_left)
{
parent = subLeft;
subLeft = subLeft->_left;
}
swap(subLeft->_key, cur->_key);
if (subLeft == parent->_left)
{
parent->_left = subLeft->_right;
}
else
{
parent->_right = subLeft->_right;
}
delete subLeft;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
BSTree() = default;//默认构造(c++11)
~BSTree()
{
Destroy(_root);
}
BSTree(const BSTree<K>& t)
{
_root = Copy(t._root);
}
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
if (root->_left == nullptr)
{
Node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
Node* del = root;
root = root->_left;
delete del;
return true;
}
else
{
Node* subLeft = root->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
swap(subLeft->_key, root->_key);
return _EraseR(root->_right, key);
}
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
}
测试:
void test1Key()
{
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
key::BSTree<int> bt;
for (auto e : a)
{
bt.Insert(e);
}
bt.InOrder();
bt.EraseR(14);
bt.InOrder();
bt.Erase(3);
bt.InOrder();
cout << bt.Find(1) << endl << bt.FindR(13) << endl << bt.Find(18) << endl;
}
void test2Key()
{
int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
key::BSTree<int> bt;
for (auto e : a)
{
bt.InsertR(e);
}
bt.InOrder();
key::BSTree<int> copy(bt);
copy.InOrder();
key::BSTree<int> bt2;
bt2 = copy;
bt2.InOrder();
}
test1Key():

test2Key():

KV模型的代码实现:
namespace key_value
{
template<class K,class V>
struct BSTreeNode
{
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
K _key;
V _value;
BSTreeNode(const K& key,const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K,class V>
class BSTree
{
typedef BSTreeNode<K,V> Node;
public:
bool Insert(const K& key,const V&value)
{
if (_root == nullptr)
{
_root = new Node(key,value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key,value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node* Find(const K& key)//通过Key找对应的Value,只需返回Key所在节点
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
Node* parent = cur;
Node* subLeft = cur->_right;
while (subLeft->_left)
{
parent = subLeft;
subLeft = subLeft->_left;
}
swap(subLeft->_key, cur->_key);
if (subLeft == parent->_left)
{
parent->_left = subLeft->_right;
}
else
{
parent->_right = subLeft->_right;
}
delete subLeft;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
Node* FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key,const V&value)
{
return _InsertR(_root, key,value);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
BSTree() = default;//默认构造(c++11)
~BSTree()
{
Destroy(_root);
}
BSTree(const BSTree<K,V>& t)
{
_root = Copy(t._root);
}
BSTree<K,V>& operator=(BSTree<K,V> t)
{
swap(_root, t._root);
return *this;
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key,root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
if (root->_left == nullptr)
{
Node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
Node* del = root;
root = root->_left;
delete del;
return true;
}
else
{
Node* subLeft = root->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
swap(subLeft->_key, root->_key);
return _EraseR(root->_right, key);
}
}
}
bool _InsertR(Node*& root, const K& key,const V&value)
{
if (root == nullptr)
{
root = new Node(key,value);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key,value);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key, value);
}
else
{
return false;
}
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
return nullptr;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return root;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":"<<root->_value<<endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
}测试:
void test1KeyValue()
{
key_value::BSTree<string, string> dict;
dict.Insert("sort", "排序");
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("insert", "插入");
dict.Insert("key", "关键字");
string str;
while (cin>>str)
{
key_value::BSTreeNode<string, string>* ret = dict.Find(str);
if (ret)
{
cout << ret->_value << endl;
}
else
{
cout << "无此单词" << endl;
}
}
}
void test2KeyValue()
{
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };
key_value::BSTree<string, int> countTree;
for (const auto& str : arr)
{
// 先查找水果在不在搜索树中
// 1、不在,说明水果第一次出现,则插入<水果, 1>
// 2、在,则查找到的节点中水果对应的次数++
key_value::BSTreeNode<string, int>* ret = countTree.Find(str);
if (ret == nullptr)
{
countTree.Insert(str, 1);
}
else
{
ret->_value++;
}
}
countTree.InOrder();
}
void test3KeyValue()
{
key_value::BSTree<string, string> dict;
dict.Insert("sort", "排序");
dict.Insert("left", "左边");
dict.Insert("right", "右边");
dict.Insert("insert", "插入");
dict.InsertR("key", "关键字");
dict.Erase("key");
dict.EraseR("insert");
dict.InOrder();
key_value::BSTreeNode<string, string> *ret = dict.Find("right");
if (ret)
{
cout << ret->_value << endl;
}
key_value::BSTreeNode<string, string>* ret2 = dict.FindR("sort");
if (ret2)
{
cout << ret2->_value << endl;
}
cout << endl;
key_value::BSTree<string, string> dict2;
dict2 = dict;
dict2.InOrder();
key_value::BSTree<string, string> dict3(dict);
dict3.InOrder();
}test1KeyValue():

test2KeyValue():

test3KeyValue():

二叉搜索树的插入和删除操作都必须先查找
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),则查找效率为O(logN)

最差情况下,二叉搜索树退化为单支树(或者类似单支),则查找效率为O(N)

退化成单支树,二叉搜索树的性能就失去了,解决方案:平衡搜索二叉树->AVL树,红黑树

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








