文章目录
1 矩阵
1.1 矩阵乘法
一个 n ∗ m n*m n∗m 阶矩阵乘一个 m ∗ k m*k m∗k 阶矩阵得到一个 n ∗ k n*k n∗k 阶矩阵
[
a
b
c
d
e
f
]
[
g
h
i
j
]
=
[
?
?
?
?
?
?
]
\begin{bmatrix} a&b\\ c&d\\ e&f \end{bmatrix} \begin{bmatrix} g&h\\ i&j\\ \end{bmatrix} = \begin{bmatrix} ?&?\\ ?&?\\ ?&?\\ \end{bmatrix}
acebdf
[gihj]=
??????

- 很简单的理解方式: 我们称横着的蓝色圈为 X X X (行向量) , 竖着的蓝色圈为 Y Y Y (列向量)
- 假设矩阵 A A A 为 n ∗ m n*m n∗m , 矩阵 B B B 为 m ∗ k m*k m∗k , 那么 A A A 提供 n n n 行 X X X , B B B 提供 k k k 列 Y Y Y
- 每个 X X X 和 Y Y Y 长度都为 m m m , 两个运算方式为 X ∗ Y = X 1 Y 1 + X 2 Y 2 + . . . + X m Y m X*Y=X_1Y_1+X_2Y_2+...+X_mYm X∗Y=X1Y1+X2Y2+...+XmYm
- 最终结果矩阵 C C C , C i , j C_{i,j} Ci,j 的结果由 A A A 的第 i i i 行 X X X 与 B B B 的第 j j j 列 Y Y Y 运算得来
for(int i=1;i<=n;i++)
for(int j=1;j<=k;j++)
for(int t=1;t<=m;t++)
C[i][j] += A[i][t]*B[t][j];
1.2 单位矩阵
-
在乘法中 a ∗ 1 = a a*1=a a∗1=a , 1 1 1 即位乘法中的单位
-
而在矩阵乘法中, 假设有矩阵 A = [ a b c d e f ] A=\begin{bmatrix} a&b&c\\ d&e&f \end{bmatrix} A=[adbecf]
-
由于矩阵乘法不具有交换律,因此有两种情况
-
若 A ∗ “ 1 ” = A A*“1”=A A∗“1”=A ,那么单位矩阵应为 3 ∗ 3 3*3 3∗3 阶的矩阵
-
而
[ a b c d e f ] [ 1 0 0 0 1 0 0 0 1 ] = [ a b c d e f ] \begin{bmatrix} a&b&c\\ d&e&f \end{bmatrix}\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}= \begin{bmatrix} a&b&c\\ d&e&f \end{bmatrix} [adbecf] 100010001 =[adbecf] -
若 “ 1 ” ∗ A = A “1”*A=A “1”∗A=A ,那么单位矩阵应为 2 ∗ 2 2*2 2∗2 阶的矩阵
-
而
[ 1 0 0 1 ] [ a b c d e f ] = [ a b c d e f ] \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}\begin{bmatrix} a&b&c\\ d&e&f \end{bmatrix}= \begin{bmatrix} a&b&c\\ d&e&f \end{bmatrix} [1001][adbecf]=[adbecf] -
对角线为 1 1 1 其余为 0 0 0 的矩阵
1.3 矩阵乘法的结合律
假设现在有三个矩阵 A , B , C A,B,C A,B,C
A : [ 1 2 1 2 1 2 ] B : [ 1 1 1 2 1 1 ] C : [ 1 1 1 1 ] A:\begin{bmatrix} 1&2&1\\ 2&1&2 \end{bmatrix} B:\begin{bmatrix} 1&1\\ 1&2\\ 1&1 \end{bmatrix} C:\begin{bmatrix} 1&1\\ 1&1 \end{bmatrix} A:[122112]B: 111121 C:[1111]
( A B ) C = [ 4 6 5 6 ] C = [ 10 10 11 11 ] (AB)C=\begin{bmatrix} 4&6\\ 5&6 \end{bmatrix}C=\begin{bmatrix} 10&10\\ 11&11 \end{bmatrix} (AB)C=[4566]C=[10111011]
A ( B C ) = A [ 2 2 3 3 2 2 ] = [ 10 10 11 11 ] A(BC)=A\begin{bmatrix} 2&2\\ 3&3\\ 2&2 \end{bmatrix}=\begin{bmatrix} 10&10\\ 11&11 \end{bmatrix} A(BC)=A 232232 =[10111011]
证明:
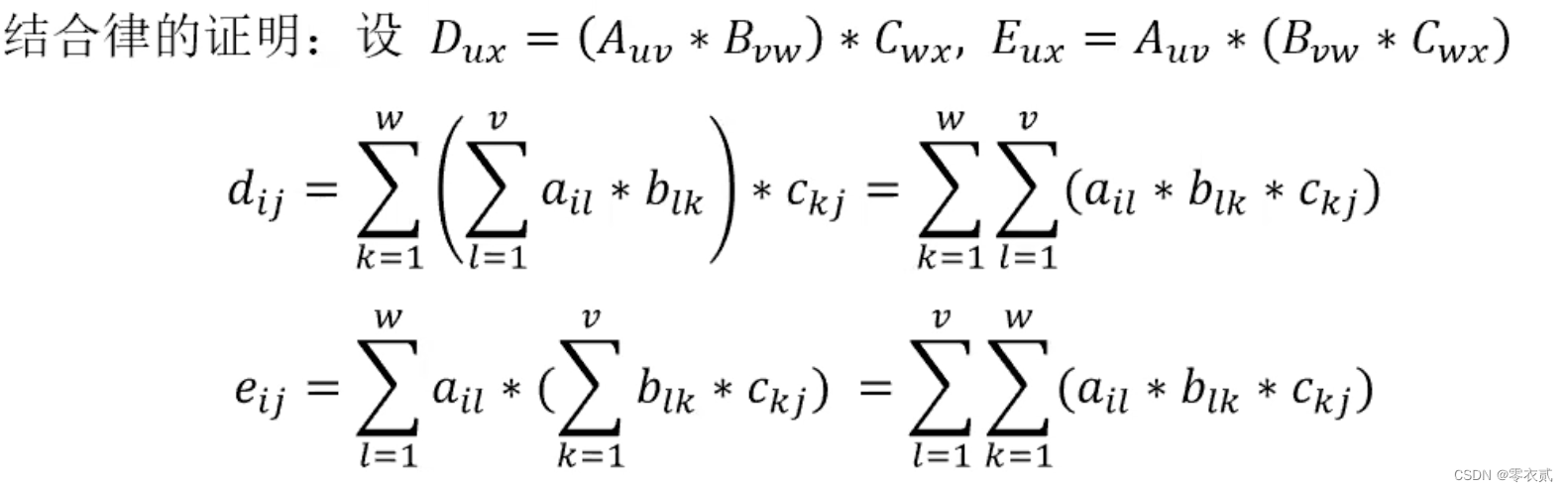
因此满足 ( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC) , 也就可以写成 A B C ABC ABC 的形式
1.4 矩阵快速幂
对于 n ∗ n n*n n∗n 的矩阵的 A A A,其可以对自身乘法,对于求 A k A^k Ak 的矩阵,可以通过快速幂优化 , 复杂度为 O ( n 3 log k ) O(n^3 \log k) O(n3logk)
struct Matrix{
int a[105][105];
Matrix() {
memset(a,0,sizeof(a));
}
}A,res;
//矩阵乘法
Matrix operator * (const Matrix &x,const Matrix &y)
{
Matrix ret;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int t=1;t<=n;t++)
ret.a[i][j] += x.a[i][t] * y.a[t][j] % mod, ret.a[i][j] %= mod;
return ret;
}
//快速幂
void qpow(Matrix a,int b)
{
Matrix base=a;
for(int i=1;i<=n;i++) res.a[i][i] = 1;//单位矩阵
while(b)
{
if(b & 1) res=res*base;
b >>= 1; base=base*base;
}
}
1.5 矩阵快速幂的应用
1.5.1
-
运用矩阵快速幂,我们可以快速求斐波那契数列的第 n n n 项
-
对于 f i f_i fi ,有 f i = f i − 1 + f i − 2 ( i ≥ 3 ) f_i=f_{i-1}+f_{i-2}\space(i\geq3) fi=fi−1+fi−2 (i≥3)
-
由于 [ f n f n − 1 ] = [ f n − 1 f n − 2 ] [ 1 1 1 0 ] = [ f n − 2 f n − 3 ] [ 1 1 1 0 ] 2 = . . . . = [ f 2 f 1 ] [ 1 1 1 0 ] n − 2 = [ 1 1 ] [ 1 1 1 0 ] n − 2 \begin{bmatrix} f_n & f_{n-1}\\ \end{bmatrix}=\begin{bmatrix} f_{n-1} & f_{n-2}\\ \end{bmatrix} \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix} =\begin{bmatrix} f_{n-2} & f_{n-3}\\ \end{bmatrix} \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^2=....=\begin{bmatrix} f_2 & f_1\\ \end{bmatrix} \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n-2}=\begin{bmatrix} 1 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 1\\ 1 & 0 \end{bmatrix}^{n-2} [fnfn−1]=[fn−1fn−2][1110]=[fn−2fn−3][1110]2=....=[f2f1][1110]n−2=[11][1110]n−2
-
用矩阵快速幂求即可,矩阵乘法不具有交换律,注意先将结果乘以 [ 1 1 ] \begin{bmatrix}1&1\\\end{bmatrix} [11]
-
复杂度为 O ( 2 3 log n ) = O ( log n ) O(2^3\log n)=O(\log n) O(23logn)=O(logn)
代码
1.5.2
-
变为 f i = p ∗ f i − 1 + q ∗ f i − 2 , f 1 = a 1 , f 2 = a 2 f_i=p*f_{i-1}+q*f_{i-2},\space f_1=a_1,\space f_2=a_2 fi=p∗fi−1+q∗fi−2, f1=a1, f2=a2 也是同理的
-
[ f n f n − 1 ] = [ f n − 1 f n − 2 ] [ p 1 q 0 ] = [ f n − 2 f n − 3 ] [ p 1 q 0 ] 2 = . . . . = [ f 2 f 1 ] [ p 1 q 0 ] n − 2 = [ a 2 a 1 ] [ p 1 q 0 ] n − 2 \begin{bmatrix} f_n & f_{n-1}\\ \end{bmatrix}=\begin{bmatrix} f_{n-1} & f_{n-2}\\ \end{bmatrix} \begin{bmatrix} p & 1\\ q & 0 \end{bmatrix} =\begin{bmatrix} f_{n-2} & f_{n-3}\\ \end{bmatrix} \begin{bmatrix} p & 1\\ q & 0 \end{bmatrix}^2=....=\begin{bmatrix} f_2 & f_1\\ \end{bmatrix} \begin{bmatrix} p & 1\\ q & 0 \end{bmatrix}^{n-2}=\begin{bmatrix} a_2 & a_1\\ \end{bmatrix} \begin{bmatrix} p & 1\\ q & 0 \end{bmatrix}^{n-2} [fnfn−1]=[fn−1fn−2][pq10]=[fn−2fn−3][pq10]2=....=[f2f1][pq10]n−2=[a2a1][pq10]n−2
代码
1.5.3
-
变为 f i = f i − 1 + f i − 3 f_i=f_{i-1}+f_{i-3} fi=fi−1+fi−3 时:
-
由于 f i f_i fi 由 f i − 1 , f i − 3 f_{i-1},f_{i-3} fi−1,fi−3 转移而来 , 因此对于 i − 1 i-1 i−1 状态一定含有 f i − 1 , f i − 3 f_{i-1},f_{i-3} fi−1,fi−3 即 对于 i i i 一定含有 f i , f i − 2 f_i,f_{i-2} fi,fi−2 而此时 f i − 2 f_{i-2} fi−2 也需转移 , 因此我们可以考虑使用 [ f i f i − 1 f i − 2 ] \begin{bmatrix} f_i & f_{i-1} & f_{i-2} \end{bmatrix} [fifi−1fi−2] 进行转移
-
[ f n f n − 1 f n − 2 ] = [ f n − 1 f n − 2 f n − 3 ] [ 1 1 0 0 0 1 1 0 0 ] = [ f n − 2 f n − 3 f n − 4 ] [ 1 1 0 0 0 1 1 0 0 ] 2 = . . . . = [ f 3 f 2 f 1 ] [ 1 1 0 0 0 1 1 0 0 ] n − 3 \begin{bmatrix} f_n & f_{n-1} & f_{n-2} \end{bmatrix}= \begin{bmatrix} f_{n-1} & f_{n-2} & f_{n-3} \end{bmatrix} \begin{bmatrix} 1 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\\ \end{bmatrix} = \begin{bmatrix} f_{n-2} & f_{n-3} & f_{n-4} \end{bmatrix} \begin{bmatrix} 1 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\\ \end{bmatrix}^2=....= \begin{bmatrix} f_{3} & f_{2} & f_{1} \end{bmatrix} \begin{bmatrix} 1 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0\\ \end{bmatrix}^{n-3} [fnfn−1fn−2]=[fn−1fn−2fn−3] 101100010 =[fn−2fn−3fn−4] 101100010 2=....=[f3f2f1] 101100010 n−3
代码
1.5.4
-
求 g c d ( f n , f m ) gcd(f_n,f_m) gcd(fn,fm)
-
g c d ( f n , f m ) = f ( g c d ( n , m ) ) gcd(f_n,f_m)=f(gcd(n,m)) gcd(fn,fm)=f(gcd(n,m))
以上 1.5.1 至 1.5.4 均为关于斐波那契的应用
1.5.5

令
f
i
f_i
fi 表示经过
i
i
i 次从
A
A
A 跳回
A
A
A 的方案数
令
g
i
g_i
gi 表示经过
i
i
i 次从
A
A
A 跳到 某一个 非
A
A
A 位置
B
B
B 的方案数
那么我们需要分别转移 f i , g i f_i,g_i fi,gi
对于
f
i
f_i
fi , 上一步一定非
A
A
A , 非
A
A
A 位置有
p
−
1
p-1
p−1 个
那么有
f
i
=
g
i
−
1
×
(
p
−
1
)
f_i=g_{i-1}\times (p-1)
fi=gi−1×(p−1)
对于
g
i
g_i
gi , 可能为
A
A
A 到
B
B
B , 有
f
i
−
1
f_{i-1}
fi−1 种
也可能非
A
A
A 位置到
B
B
B , 此情况非
A
A
A 位置有
p
−
2
p-2
p−2 个 , 有
(
p
−
2
)
×
g
i
−
1
(p-2)\times g_{i-1}
(p−2)×gi−1 种
因此 :
g
i
=
f
i
−
1
+
g
i
−
1
×
(
p
−
2
)
g_i=f_{i-1}+g_{i-1}\times (p-2)
gi=fi−1+gi−1×(p−2)
f
i
=
g
i
−
1
×
(
p
−
1
)
f_i=g_{i-1}\times (p-1)
fi=gi−1×(p−1)
g
i
=
f
i
−
1
+
g
i
−
1
×
(
p
−
2
)
g_i=f_{i-1}+g_{i-1}\times (p-2)
gi=fi−1+gi−1×(p−2)
[ f i g i ] = [ f i − 1 g i − 1 ] [ 0 1 p − 1 p − 2 ] = [ f i − 2 g i − 2 ] [ 0 1 p − 1 p − 2 ] 2 = . . . \begin{bmatrix} f_i & g_i \end{bmatrix}= \begin{bmatrix} f_{i-1} & g_{i-1} \end{bmatrix}\begin{bmatrix} 0 & 1\\ p-1 & p-2 \end{bmatrix}= \begin{bmatrix} f_{i-2} & g_{i-2} \end{bmatrix}\begin{bmatrix} 0 & 1\\ p-1 & p-2 \end{bmatrix}^2=... [figi]=[fi−1gi−1][0p−11p−2]=[fi−2gi−2][0p−11p−2]2=...
初始 : f 0 = 1 , g 0 = 0 f_0=1,g_0=0 f0=1,g0=0 , 矩阵快速幂即可
1.5.6

a n + b n = ( a n − 1 + b n − 1 ) ( a + b ) − ( a n − 2 + b n − 2 ) a b a^n+b^n=(a^{n-1}+b^{n-1})(a+b)-(a^{n-2}+b^{n-2})ab an+bn=(an−1+bn−1)(a+b)−(an−2+bn−2)ab
记 f n = a n + b n f_n=a^n+b^n fn=an+bn , f n = p × f n − 1 − q × f n − 2 f_n=p\times f_{n-1}-q\times f_{n-2} fn=p×fn−1−q×fn−2
[ f n f n − 1 ] = [ f n − 1 f n − 2 ] [ p 1 − q 0 ] = [ f n − 2 f n − 3 ] [ p 1 − q 0 ] 2 = . . . \begin{bmatrix} f_n & f_{n-1}\\ \end{bmatrix}=\begin{bmatrix} f_{n-1} & f_{n-2}\\ \end{bmatrix} \begin{bmatrix} p & 1\\ -q & 0 \end{bmatrix}= \begin{bmatrix} f_{n-2} & f_{n-3} \end{bmatrix} \begin{bmatrix} p & 1\\ -q & 0 \end{bmatrix}^2=... [fnfn−1]=[fn−1fn−2][p−q10]=[fn−2fn−3][p−q10]2=...
初始 : f 1 = 1 , f 0 = 2 f_1=1, f_0=2 f1=1,f0=2
即转为 1.5.2
1.5.7
N N N 个点 M M M 条边的无重边有向图,点的编号为 1 − N 1-N 1−N,边权表示通过这条边所需时间(秒),从 1 1 1 出发经过 S S S 秒后到达 N N N ,问走法方案数 N ≤ 8 , M ≤ 15 , S ≤ 2 × 1 0 9 , 边权 ≤ 9 N\le8,M\le15,S\le2\times10^9,{边权}\le9 N≤8,M≤15,S≤2×109,边权≤9
记 F i = [ f 1 f 2 . . . . f N ] F_i=\begin{bmatrix} f_1 & f_2 & .... &f_N\\ \end{bmatrix} Fi=[f1f2....fN] 表示第 i i i 秒 , 到达 1 − n 1-n 1−n 的方案数
若边权均为 1 1 1 , 记 A A A 为邻接矩阵 , 那么 F N = F N − 1 A = . . . = F 0 A n F_N=F_{N-1}A=...=F_0A^n FN=FN−1A=...=F0An , F 0 = [ 1 0 . . . . 0 ] F_0=\begin{bmatrix} 1 & 0 & .... &0\ \end{bmatrix} F0=[10....0 ]
我们考虑将边权非 1 1 1 的转换为 1 1 1 的 , 例如 A → B A\to B A→B 边权为 w w w , 我们将其转化为 A → x 1 → x 2 → . . . → x w → B A\to x_1\to x_2\to ... \to x_w \to B A→x1→x2→...→xw→B , 其中 x x x 为虚点 , 即化为上述情况. 注意虚点空间 , 建 9 × 15 9\times15 9×15 左右
2.动态dp
动态dp就是一类带修改操作的dp问题
2.1 静态查询最大子段和
- f i = m a x ( f i − 1 + a i , a i ) f_i=max(f_{i-1}+a_i,\space a_i) fi=max(fi−1+ai, ai)
- 最终结果即为 m a x ( f i ) max(f_i) max(fi) , 也可以表示为 a n s i = m a x ( a n s i − 1 , f i ) ans_i=max(ans_{i-1},\space f_i) ansi=max(ansi−1, fi)
2.2 静态查询区间最大子段和
-
比较传统的做法是用线段树维护 代码
-
在此提供矩阵做法
-
常规的矩阵:
-
[ a b c d ] [ 1 2 ] = [ a + 2 b c + 2 d ] \begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} 1\\ 2 \end{bmatrix}=\begin{bmatrix} a+2b\\ c+2d \end{bmatrix} [acbd][12]=[a+2bc+2d]
- 我们定义一种新的矩阵,运算方式如下:
- [ a b c d ] [ 1 2 ] = [ m a x ( a + 1 , b + 2 ) m a x ( c + 1 , d + 2 ) ] \begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} 1\\ 2 \end{bmatrix}=\begin{bmatrix} max{(a+1,b+2)}\\ max(c+1,d+2) \end{bmatrix} [acbd][12]=[max(a+1,b+2)max(c+1,d+2)]
- A : [ 1 2 2 4 ] B : [ 1 1 1 2 ] C : [ 1 1 ] A:\begin{bmatrix} 1&2\\ 2&4 \end{bmatrix} B:\begin{bmatrix} 1&1\\ 1&2 \end{bmatrix} C:\begin{bmatrix} 1\\ 1 \end{bmatrix} A:[1224]B:[1112]C:[11]
- ( A B ) C = [ 3 4 5 6 ] C = [ 5 7 ] (AB)C=\begin{bmatrix} 3&4\\ 5&6 \end{bmatrix}C=\begin{bmatrix} 5\\ 7 \end{bmatrix} (AB)C=[3546]C=[57]
- A ( B C ) = A [ 2 3 ] = [ 5 7 ] A(BC)=A\begin{bmatrix} 2\\ 3 \end{bmatrix}=\begin{bmatrix} 5\\ 7 \end{bmatrix} A(BC)=A[23]=[57]
- 新定义的矩阵同样具有结合律
-
根据 f i = m a x ( f i − 1 + a i , a i ) f_i=max(f_{i-1}+a_i,\space a_i) fi=max(fi−1+ai, ai)
-
得 [ f i 0 ] = [ a i a i − ∞ 0 ] [ f i − 1 0 ] \begin{bmatrix} f_i \\ 0 \end{bmatrix}= \begin{bmatrix} a_i & a_i\\ -\infin & 0 \end{bmatrix} \begin{bmatrix} f_{i-1}\\ 0 \end{bmatrix} [fi0]=[ai−∞ai0][fi−10]
-
然而仅仅知道 f i f_i fi 的值是不够的,最终结果为 m a x ( f i ) ( L ≤ i ≤ R ) max(f_i)(L\leq i \leq R) max(fi)(L≤i≤R) ,我们考虑将 a n s i ans_i ansi 也加入矩阵, a n s i = m a x ( a n s i − 1 , f i ) , f i = m a x ( f i − 1 + a i , a i ) ans_i=max(ans_{i-1},\space f_i),\space f_i=max(f_{i-1}+a_i,\space a_i) ansi=max(ansi−1, fi), fi=max(fi−1+ai, ai)
-
[ a n s i f i 0 ] = [ 0 a i a i − ∞ a i a i − ∞ − ∞ 0 ] [ a n s i − 1 f i − 1 0 ] \begin{bmatrix} ans_i\\ f_i \\ 0 \end{bmatrix}= \begin{bmatrix} 0 & a_i & a_i\\ -\infin & a_i & a_i\\ -\infin & -\infin & 0 \end{bmatrix} \begin{bmatrix} ans_{i-1}\\ f_{i-1}\\ 0 \end{bmatrix} ansifi0 = 0−∞−∞aiai−∞aiai0 ansi−1fi−10
-
我们假设 [ 0 a i a i − ∞ a i a i − ∞ − ∞ 0 ] \begin{bmatrix} 0 & a_i & a_i\\ -\infin & a_i & a_i\\ -\infin & -\infin & 0 \end{bmatrix} 0−∞−∞aiai−∞aiai0 为 A i A_i Ai
-
若当前询问区间为 [ L , R ] [L,R] [L,R]
-
那么 [ a n s R f R 0 ] = A R [ a n s R − 1 f R − 1 0 ] = A R A R − 1 [ a n s R − 2 f R − 2 0 ] = . . . = A R A R − 1 A R − 2 . . . A L + 1 [ a n s L f L 0 ] \begin{bmatrix} ans_R\\ f_R\\ 0 \end{bmatrix}= A_{R} \begin{bmatrix} ans_{R-1}\\ f_{R-1}\\ 0 \end{bmatrix}= A_{R}A_{R-1} \begin{bmatrix} ans_{R-2}\\ f_{R-2}\\ 0 \end{bmatrix}=...= A_RA_{R-1}A_{R-2}...A_{L+1} \begin{bmatrix} ans_L\\ f_L\\ 0 \end{bmatrix} ansRfR0 =AR ansR−1fR−10 =ARAR−1 ansR−2fR−20 =...=ARAR−1AR−2...AL+1 ansLfL0
-
而 a n s L = f L = a L ans_L=f_L=a_L ansL=fL=aL
-
所以 [ a n s L f L 0 ] = A L [ − ∞ 0 0 ] \begin{bmatrix} ans_L\\ f_L\\ 0 \end{bmatrix}=A_{L} \begin{bmatrix} -\infin\\ 0\\ 0 \end{bmatrix} ansLfL0 =AL −∞00
-
原式 = A R A R − 1 A R − 2 . . . A L [ − ∞ 0 0 ] =A_RA_{R-1}A_{R-2}...A_{L} \begin{bmatrix} -\infin\\ 0\\ 0 \end{bmatrix} =ARAR−1AR−2...AL −∞00
-
我们只需维护某一区间矩阵的乘积即可,最终结果为 a n s R ans_R ansR ,可使用线段树维护区间 A A A 的乘积 ,注意矩阵乘法没有交换律
2.3 动态查询区间最大子段和
单点修改
对于传统线段树做法 : 代码
对于矩阵做法 : 代码
2.4 树上动态查询链上最大子段和
-
根据 2.2 2.3 的思路 , 不难想到用树链剖分转化为线性并用线段树维护
-
查询操作 : 对于一条路径 , 我们将其拆分成若干条重链 , 答案为这条路径上路径上矩阵 A A A 的积乘以 [ − ∞ 0 0 ] \begin{bmatrix} -\infin\\ 0\\ 0 \end{bmatrix} −∞00 也就是这若干条重链的 A A A 乘积 , 注意矩阵乘法的顺序
-
区间修改操作 : 将 x → y x\to y x→y 路径上的所有 a i a_i ai 变为 k k k . 例如对某一区间进行修改 , 那么该区间就变为 [ 0 k k − ∞ k k − ∞ − ∞ 0 ] b \begin{bmatrix} 0 & k & k\\ -\infin & k & k\\ -\infin & -\infin & 0 \end{bmatrix}^b 0−∞−∞kk−∞kk0 b 对此若直接使用矩阵快速幂是可以的 , 单次 pushdown 时间复杂度为 O ( 3 3 ∗ log n ) O(3^3*\log n) O(33∗logn) , 总时间复杂度为 O ( 3 3 ∗ Q ∗ log 3 n ) O(3^3*Q*\log^3 n) O(33∗Q∗log3n).但有更为优秀的做法 : 观察 A i b A_i^b Aib 发现 :
a i ≥ 0 a_i\geq0 ai≥0 时 , A i b = [ 0 b a i b a i − ∞ b a i b a i − ∞ − ∞ 0 ] A_i^b=\begin{bmatrix} 0 & ba_i & ba_i\\ -\infin & ba_i & ba_i\\ -\infin & -\infin & 0 \end{bmatrix} Aib= 0−∞−∞baibai−∞baibai0 ,
a i < 0 a_i<0 ai<0 时 , A i b = [ 0 a i a i − ∞ b a i a i − ∞ − ∞ 0 ] A_i^b=\begin{bmatrix} 0 & a_i & a_i\\ -\infin & ba_i & a_i\\ -\infin & -\infin & 0 \end{bmatrix} Aib= 0−∞−∞aibai−∞aiai0 -
就查询操作而言,时间复杂度便优化到了 O ( 3 3 ∗ log 2 n ) O(3^3*\log^2 n) O(33∗log2n)
代码(没过)
3.矩阵进阶
3.1 逆矩阵
对于 n n n 阶矩阵 A A A , 若存在 n n n 阶矩阵 B B B 使得 A B = B A = I n AB=BA=I_n AB=BA=In , I n I_n In 为 n n n 阶单位矩阵 , 那么 A A A 称为可逆矩阵 , B B B 为 A A A 的逆矩阵
性质:
-
逆矩阵是唯一的
证明 : 若存在不同的矩阵 B , C B,C B,C 使得 A B = I , A C = I AB=I,AC=I AB=I,AC=I , 那么 A B = A C AB=AC AB=AC , 则 B = C B=C B=C , 矛盾
-
( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
-
转置矩阵 A T A^T AT 表示 A A A 沿对角线对称的矩阵 , ( A − 1 ) T = ( A T ) − 1 (A^{-1})^T=(A^T)^{-1} (A−1)T=(AT)−1
-
( A B ) − 1 = A − 1 B − 1 (AB)^{-1}=A^{-1}B^{-1} (AB)−1=A−1B−1 证明 : A B ( A B ) − 1 = I AB(AB)^{-1}=I AB(AB)−1=I , ( A B ) − 1 = A − 1 B − 1 (AB)^{-1}=A^{-1}B^{-1} (AB)−1=A−1B−1
3.2 行列式
-

-

-
计算过程 : 先写出 n ! n! n! 项 1 1 1 到 n n n 的全排列 , 然后计算这 n ! n! n! 项排列中的逆序对 , 然后带入计算得出这一项排列的乘积 (感性理解 : 排列用于确定每一行的列) , 最终加和
例如 :
d e t ( A ) = ∣ 1 3 1 2 1 3 4 2 1 ∣ det(A)=\begin{vmatrix} 1 & 3 & 1\\ 2 & 1 & 3\\ 4 & 2 & 1 \end{vmatrix} det(A)= 124312131
1
,
2
,
3
1,2,3
1,2,3 :
(
−
1
)
0
×
a
11
×
a
22
×
a
33
=
1
(-1)^0\times a_{11}\times a_{22}\times a_{33} =1
(−1)0×a11×a22×a33=1
1
,
3
,
2
1,3,2
1,3,2 :
(
−
1
)
1
×
a
11
×
a
23
×
a
32
=
−
6
(-1)^1\times a_{11}\times a_{23}\times a_{32} =-6
(−1)1×a11×a23×a32=−6
2
,
1
,
3
2,1,3
2,1,3 :
(
−
1
)
1
×
a
12
×
a
21
×
a
33
=
−
6
(-1)^1\times a_{12}\times a_{21}\times a_{33} =-6
(−1)1×a12×a21×a33=−6
2
,
3
,
1
2,3,1
2,3,1 :
(
−
1
)
2
×
a
12
×
a
23
×
a
31
=
36
(-1)^2\times a_{12}\times a_{23}\times a_{31} =36
(−1)2×a12×a23×a31=36
3
,
1
,
2
3,1,2
3,1,2 :
(
−
1
)
2
×
a
13
×
a
21
×
a
32
=
4
(-1)^2\times a_{13}\times a_{21}\times a_{32} =4
(−1)2×a13×a21×a32=4
3
,
2
,
1
3,2,1
3,2,1 :
(
−
1
)
3
×
a
13
×
a
22
×
a
31
=
−
4
(-1)^3\times a_{13}\times a_{22}\times a_{31} =-4
(−1)3×a13×a22×a31=−4
d e t ( A ) = 25 det(A)=25 det(A)=25
-
性质 :
-
A A A 中某一行的数乘以 k k k , 则 d e t ( A ) → k × d e t ( A ) det(A)\to k \times det(A) det(A)→k×det(A) (每一项排列必定包含该行的某一个数 , 因此每一项排列就都乘以了 k k k , 因此总和乘以 k k k)
-
d e t ( A ) = d e t ( A T ) det(A)=det(A^T) det(A)=det(AT)
-
A A A 的两行成比例 , 其行列式值为 0 0 0 , 以 2 2 2 阶行列式为例 : ∣ a b k a k b ∣ \begin{vmatrix} a & b\\ ka & kb \end{vmatrix} akabkb , k a b + ( − k a b ) = 0 kab+(-kab)=0 kab+(−kab)=0 (两列同理)
-
-
将 A A A 的某两行互换 , d e t ( A ′ ) = − d e t ( A ) det(A')=-det(A) det(A′)=−det(A)
例如 : d e t ( A ) = ∣ 1 3 1 2 1 3 4 2 1 ∣ → ∣ 4 2 1 2 1 3 1 3 1 ∣ det(A)=\begin{vmatrix} 1 & 3 & 1\\ 2 & 1 & 3\\ 4 & 2 & 1 \end{vmatrix} \to \begin{vmatrix} 4 & 2 & 1\\ 2 & 1 & 3\\ 1 & 3 & 1 \end{vmatrix} det(A)= 124312131 → 421213131
1 , 2 , 3 1,2,3 1,2,3 : 1 → 4 1 \to4 1→4
1 , 3 , 2 1,3,2 1,3,2 : − 6 → − 36 -6\to-36 −6→−36
2 , 1 , 3 2,1,3 2,1,3 : − 6 → − 4 -6\to-4 −6→−4
2 , 3 , 1 2,3,1 2,3,1 : 36 → 6 36\to6 36→6
3 , 1 , 2 3,1,2 3,1,2 : 4 → 6 4\to6 4→6
3 , 2 , 1 3,2,1 3,2,1 : − 4 → − 1 -4\to-1 −4→−1d e t ( A ) : 25 → − 25 det(A):25\to -25 det(A):25→−25
由于某项排列可以理解为第 i i i 行的列数 , 如上例中调换 1 , 3 1,3 1,3 行相当于将排列中第 1 , 3 1,3 1,3 位置调换 , 发现逆序对数量奇偶性一定发生变化
(两列同理)
3.3 矩阵的初等变换
矩阵的初等变换 : 矩阵的初等行变换以及列变换








 文章介绍了矩阵的基本概念,包括矩阵乘法、单位矩阵和矩阵乘法的结合律,并探讨了矩阵快速幂及其在斐波那契数列、动态规划问题中的应用。此外,还讨论了动态dp策略,如静态查询最大子段和、动态查询区间最大子段和,以及树上动态查询链上最大子段和的问题。
文章介绍了矩阵的基本概念,包括矩阵乘法、单位矩阵和矩阵乘法的结合律,并探讨了矩阵快速幂及其在斐波那契数列、动态规划问题中的应用。此外,还讨论了动态dp策略,如静态查询最大子段和、动态查询区间最大子段和,以及树上动态查询链上最大子段和的问题。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








