【算法通关村】算法通关村——位运算

二进制表示数

机器数：一个数在计算机中的二进制表示形式。带符号，最高位表示符号。正数0，负数1。

真值：去掉符号位，表示的数。

原码：符合位+真值绝对值。

反码：正数，本身。负数，符号位不变，其余取反。

补码：正数，本身。负数，原码基础上，符号位不变，其余取反，最后+1。

为什么会有反码和补码？

人觉得原码挺好，根据符合位判断符合，根据真值计算加减。

但是计算机，只会加法，1-1==1+(-1)=0，这样设计简单。

-0是什么？好奇怪，0没有符号，但是有两种表示方式，00000000，10000000，好浪费啊。

于是补码来了

完美！

除此之外，这样0用00000000表示，而1000000可以表示-128

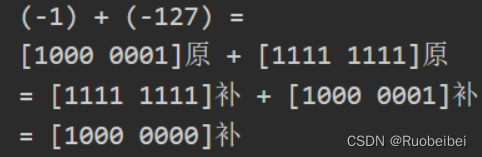
这样使用补码表示的范围为[-128,127]。

32位int类型，可以表示范围是[-2^{31} ,2^{31}]。

位运算规则

与、或、异或和取反

移位运算

左移右移。算术移位逻辑移位。

• 左移，高位丢弃，低位补0。算术移位<<和逻辑<<<移位相同。

• 右移，低位丢弃，高位补位：

  • 算术右移>>，考虑符号位，高位补符号位；

  • 逻辑右移>>>，高位补0。

  • 0和正数，算术右移和逻辑右移的结果是相同的。

移位运算与乘除法的关系

左移，乘法。将一个数左移k位，等价于将这个数乘以2^k。当乘数不是2的整数次幂时，可以将乘数拆成若干项2的整数次幂之和，例如，a*6等价于(a<<2)+(a<<1)。

右移，除法。同理。结果向下取整。