杨辉三角的实现

杨辉三角的简单介绍

杨辉三角，是二项式系数在三角形中的一种几何排列，中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623----1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。 

它的性质有

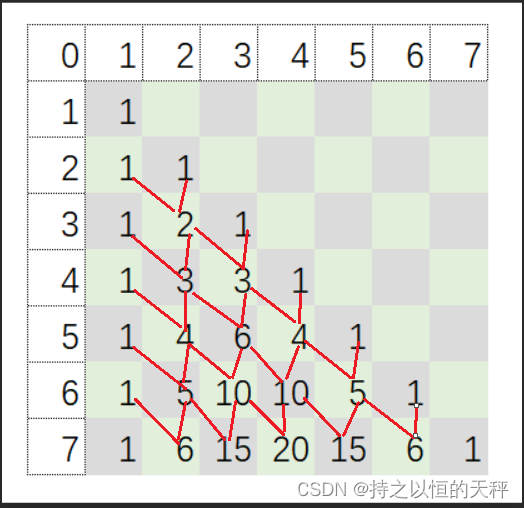
1. 每个数等于它上方两数之和。

2. 每行数字左右对称，由1开始逐渐变大。

3. 第n行的数字有n项。

4. 前n行共[(1+n)n]/2 个数。

5. 第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

如图所示

思路解析

我们可以定义行为 i ，列为 j ，当 j ==0时和 i ==j 时都为1，而其他行和列满足一定的规律，就是

arr[i][j]=arr[i-1][j-1]+arr[i-1][j],这样我们就能写出代码了

int main()
{
	int arr[10][10] = { 0 };
	int n = 0;
	printf("输入你要打印的行数：");
	scanf("%d", &n);
	int i, j = 0;
	for (i = 0; i < n; i++)
	{
		for (j = 0; j <= i; j++)
		{
			if (j == 0 || j == i)
			{
				arr[i][j] = 1;
				printf("%d ", arr[i][j]);
			}
			else
			{
				arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
				printf("%d ", arr[i][j]);
			}
		}
		printf("\n");
	}
	return 0;
}

当然还能用递归来实现，因为第一行和第二行都是1，所以我们可以根据这个来知道递归的终止条件。 

#include<stdio.h>
int cnt(int i, int j)
{
	if (j == i || j == 0)
		return 1;
	else
		return cnt(i - 1, j - 1) + cnt(i - 1, j);
}
void Yang_Hui_Triangle(int n)
{
	int i, j = 0;
	for (i = 0; i < n; i++)
	{
		for (j = 0; j <= i; j++)
		{
			printf("%d ", cnt(i, j));
		}
		printf("\n");
	}
	
}
int main()
{
	int arr[10][10] = { 0 };
	int n = 0;
	printf("输入你要打印的行数：");
	scanf("%d", &n);
	Yang_Hui_Triangle(n);
	return 0;
}