【字典树】Trie树

场景：

维护一个字符串集合，支持两种操作：

1. I向集合中插入一个字符串 x；
2. Q询问一个字符串在集合中出现了多少次。

共有 N 个操作，所有输入的字符串总长度不超过 1e5，字符串仅包含小写英文字母。

举例：存入abcd，abc，abe，ba，bbd，bc，到集合中

字典树，英文名Trie，如其名：就是一棵像字典一样的树。

配合上方例子，字典树结构如下:

 

 

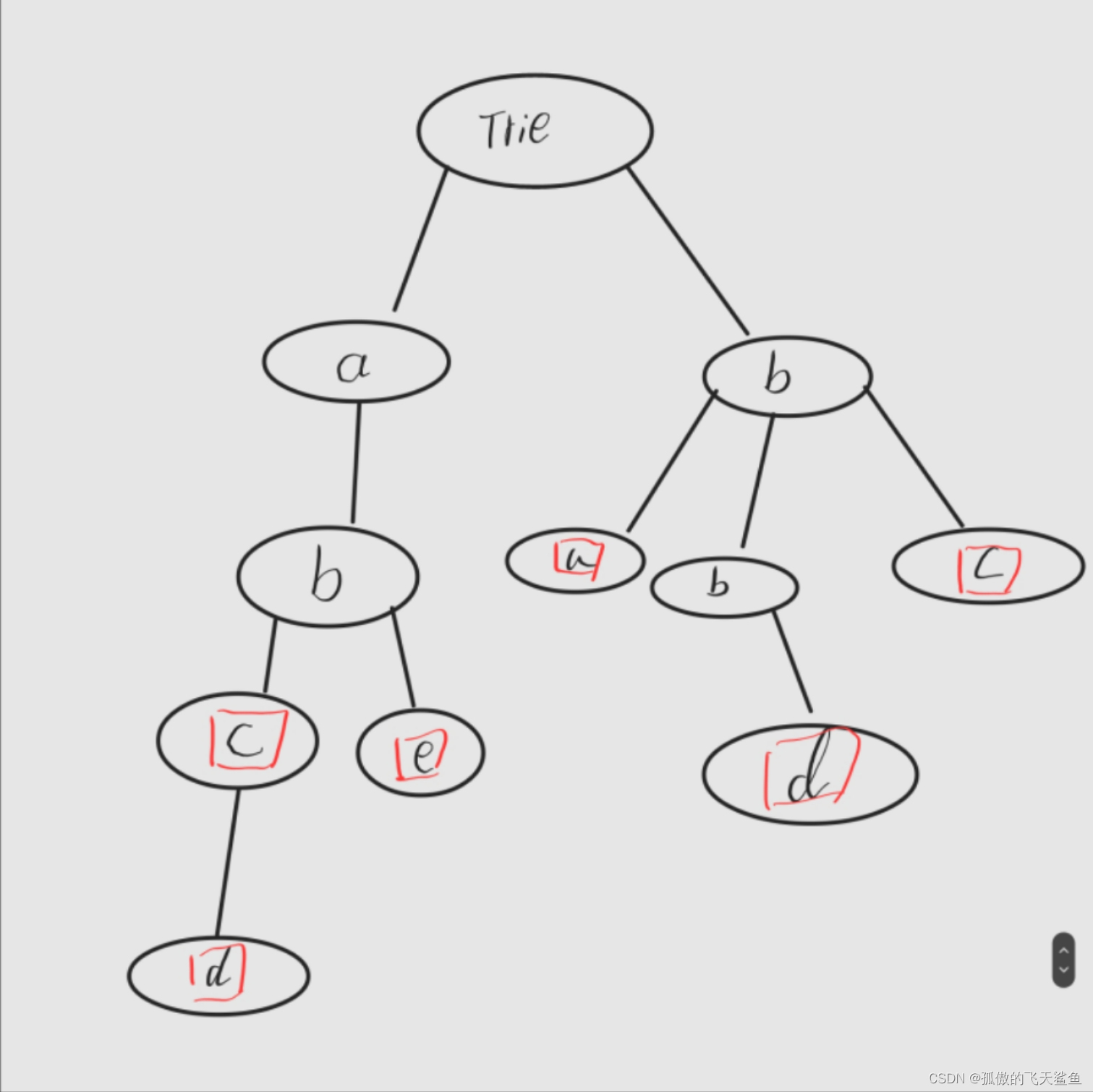
原理讲解

图中，红框节点是一个字符串的终点字母，执行查询操作时，例如查询"abe"字符串，从根节点出发，存在a节点，走到a节点，再往下存在b节点，走到b节点，接着存在e节点，继续走到e节点，到此走完了abe三步，同时e是红框节点。查询操作结束，返回"abe"字符串存在的结果，若查询的是"ab"字符串，走到b结点时，发现此点不是结束点，返回字符串不存在的结果；当然，像"abed"这种字符串，走到c点时，发现后继不存在d，返回该字符串不存在即可；

代码

了解完基本用法原理，接下来试着完成代码；

先给出代码，紧接着解释

const int N=1000010;

int trie[N][26];
int idx;
int cnt[N];
int n;

void insert(string s);

int find(string s);

int main()
{
	scanf("%d",&n);
	while(n--)
	{
		char opt;
		string s;
		cin>>op;
		cin>>s;
		if(opt=='I')
		insert(s);
		else if(opt=='Q')
		cout<<find(s)<<endl;
	}
	
	return 0;
 } 
 void insert(string s)
{
	int p=0;
	for(int i=0;i<s.size();i++)
	{
		int x=s[i]-'a';
		if(trie[p][x]==0)trie[p][x]=++idx;
		p=trie[p][x];
	}
	cnt[p]++;
}
int find(string s)
{
	int p=0;
	for(int i=0;i<s.size();i++)
	{
		int x=s[i]-'a';
		if(trie[p][x]==0)return 0;
		p=trie[p][x];
	}
	return cnt[p];
}

解释：

①trie[p][x]：用一个二维数组实现树，trie[p][x],其中[p]表示该节点的位置，[x]表示该点有一个儿子p，trie[p][x],的值表示这个[p]儿子所在的位置，举个例子：trie[0][1]=2表示根节点下有一个儿子‘b’，儿子'b'的位置为2，trie[2][0]=8表示 根结点儿子'b'（即位置为3的结点）它有一个儿子'a'，位置在8；

②idx：全局变量，记录当前的结点个数，作用如果不理解建议先放下，通过对整体代码的阅读来理解idx；

③cnt[x]：记录每个字符串出现的次数

④函数中的变量p：表示当前位置，初始为0，通过[p]索引，判断节点是否存在，本轮循环结束时通过trie[p][x]的值更新到儿子的位置，此变量难度较高，建议通过对代码的整体的阅读和执行过程模拟，去深入理解[p]；