机器学习-支持向量机

在我看来，支持向量机是机器学习里面一个比较难以理解的算法，如何要理解非常透彻，对高数要求要好，因为里面涉及到一些拉格朗日乘法、泰勒级数等，所以我也没有对其进行深入理解，但是面试官会经常涉及到关于支持向量机的一些问题，当然这个算法也是很强大的，学习也是非常必要的。首先就要了解什么是支持向量机，支持向量机是干什么的，大致是怎么实现的。

支持向量机是机器学习中的一种监督学习，它既可以解决分类问题，也可以解决回归问题，以分类问题为例，如下图：

对于一个二分类问题，我们可能会有像H2、H3或者更多这样的决策边界，但是这些决策边界中哪个是最好的一个呢？直观来看，应该取H3那条红线，因为这条线对样本的“容忍性”最好，也就是说样本发生微小变化，不会影响分类结果，但是其他细线，如果样本发生微小变化，都会使得分类结果发生变化，也就是说H3作为决策边界，其鲁棒性最好。而支持向量机所做的就是根据离决策边界最近的数据与决策边界的距离越大越好。

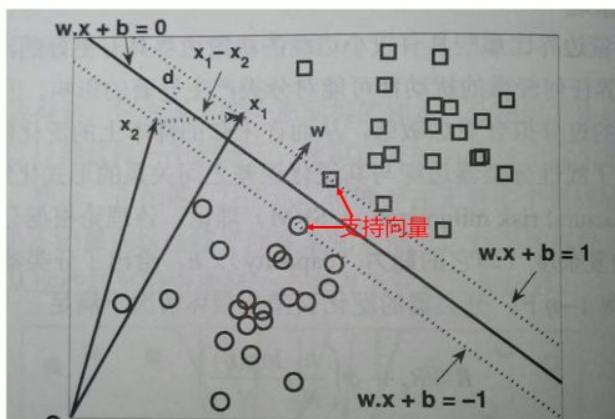
其中离决策边界最近的两个点就叫做支持向量，也叫做支撑向量，所以支持向量机有时也可以叫做支撑向量机。其中如何寻找最优决策边界就涉及到了一些数学方法，还是比较麻烦的。

在实际问题中，我们会经常遇到一些非线性情况，原先在一维空间中我们不可能画一个直线或者一个平面将样本点分类，通过转化到二维空间就变得线性可分。
总结：样本点在低维空间中线性不可分,通过将低维空间的非线性问题映射到高维空间中，就变成线性可分的。

样本点原先在二维空间中找不到一个直线将其分类(非线性情况)，通过映射到三维空间。我们就可以很容易找到一个平面将其分隔开(线性情况)。

为什么低维数据升级到高维数据之后，就可以把低维度数据线性可分？在提升维度后，原本非线性的数据点变得线性可分，这在数学上是有严格证明的，即Cover定理。Cover定理可以定性地描述为：将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的，当空间的维数D越大时，在该空间的N个数据点间的线性可分的概率就越大。所以人们就努力的寻找一种映射，这映射能将样本从原始空间(低维数据)转变到高维特征空间，从而把低维空间中线性不可分的两类点变成线性可分的。这种映射ϕ(X) 又可称为“特征构建”，映射后的向量可称之为“特征向量”。幸运的是，在计算中发现，我们需要的只是两个向量在新的映射空间中的内积结果，而映射函数到底是怎么样的其实并不需要知道。于是这样就引入了核函数的概念。

支持向量机对于离群点是非常敏感的，由上述可知SVM要基于分类完全正确的基础上才能实现，所以支持向量机中还有一个非常重要的概念叫做松弛因子，之前要求把两类完全分开，我们感觉这个要求过于严格了，我们可以放松一点要求，对于一些噪音点也可以放松一点

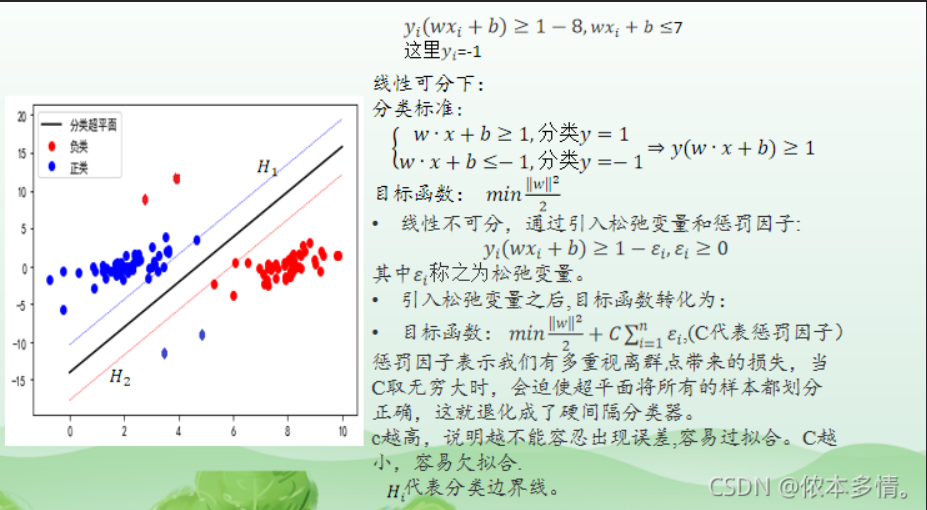
所以我们就可以改进目标函数，就像加入正则项惩罚系数一样，我们加入松弛因子，其中C就是我们需要指定的一个参数，当C很大时，伊姆西隆就要尽可能小，说明我们此时要求很严格，不能有错误，当C很小时，意味着我们可以接受一些错误。在原始的低维空间中，样本线性的不可分，无论你怎么找分类平面，总会有大量的离群点，此时用核函数向高维空间映射一下，虽然结果仍然是不可分的，但比原始空间里的要更加接近线性可分的状态（就是达到了近似线性可分的状态），此时再用松弛变量处理那些少数“冥顽不化”的离群点，就简单有效得多。